Quick BI的可视分析之路

简介： Quick BI是专为云上用户量身打造的智能数据分析和可视化BI产品，帮助企业快速完成从传统的数据分析到数据云化+分析云化的转变，将企业的业务数据产出后以最快的速度被推送到各组织侧消费使用。本篇着重介绍Quick BI在可视化分析上的能力与演进之路。

Quick BI是专为云上用户量身打造的智能数据分析和可视化BI产品，帮助企业快速完成从传统的数据分析到数据云化+分析云化的转变，将企业的业务数据产出后以最快的速度被推送到各组织侧消费使用。

本篇着重介绍Quick BI在可视化分析上的能力与演进之路。

Quick BI可视分析的能力图谱

传统的报表的结果是对统计模型的解释而不是对业务的解释。所以对可视分析的期望，为企业各个业务系统提供描述、诊断、预测等数据洞察能力的不是报表，而是带有分析（洞察）和叙事能力（见解）的 DataStorytelling，Quick BI的可视化的定义也从「可视化图表」延展为「洞察+解读」。

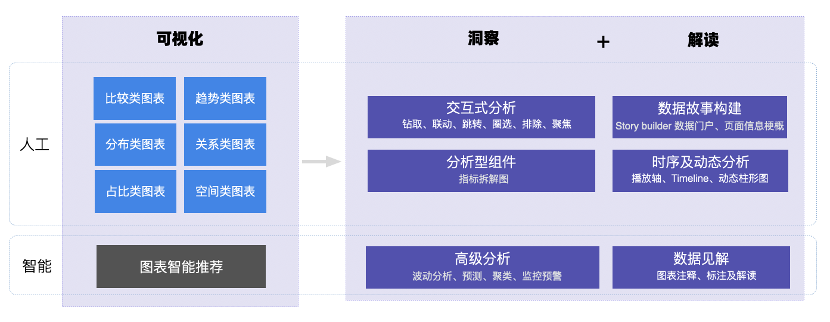
Part1 可视化

Quick BI的可视化包含可视化图表，和模板、主题；主题支持6套默认主题背景（包含深浅皮肤色），以及用户自定义主题，适应不同的产品风格。

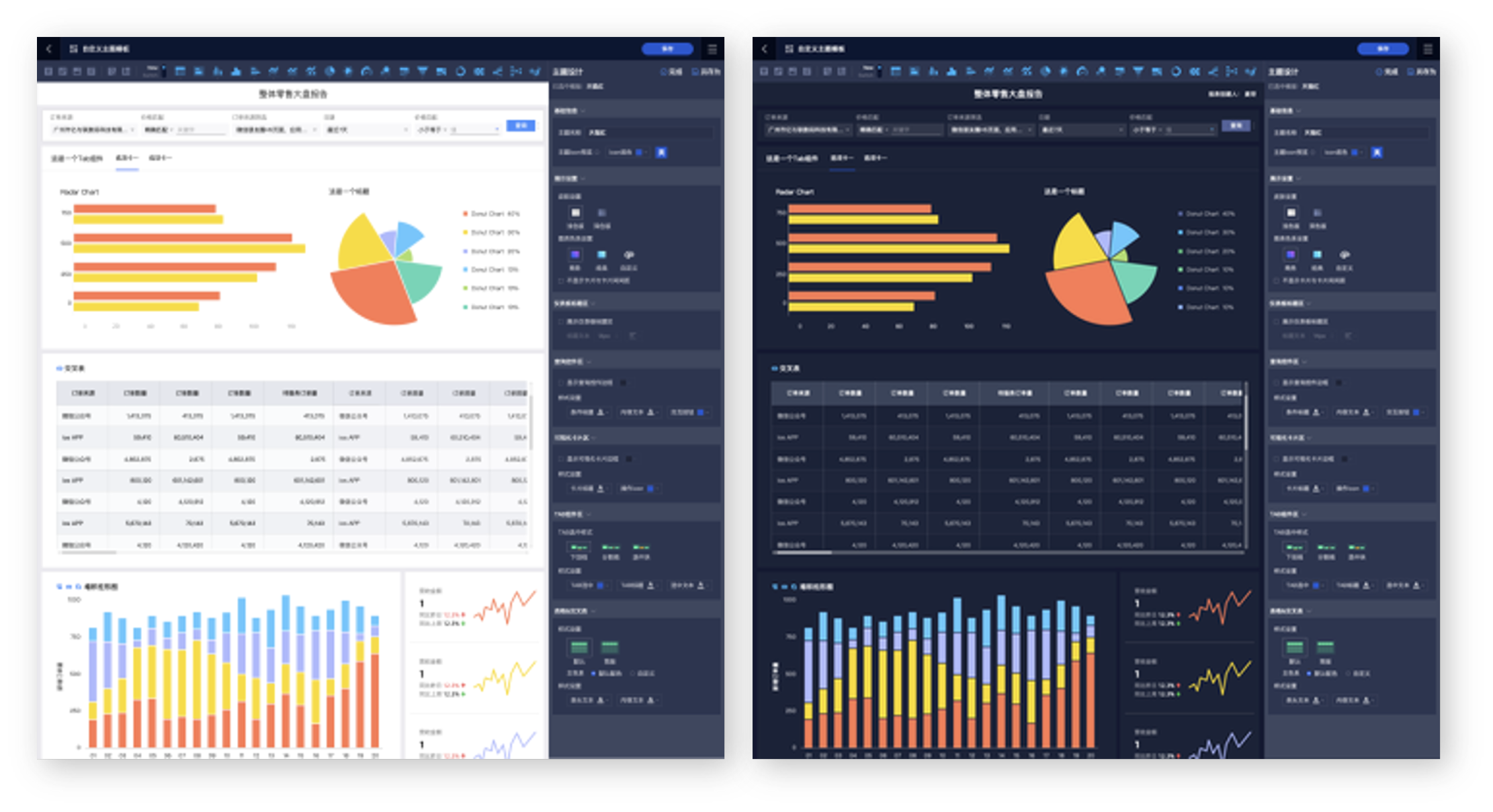
其中可视化图表按照分析意图分为比较类图表、趋势类图表、分布类图表、关系类图表、占比类图表、空间类图表，详细的后续会在另外一篇可视化中展开。

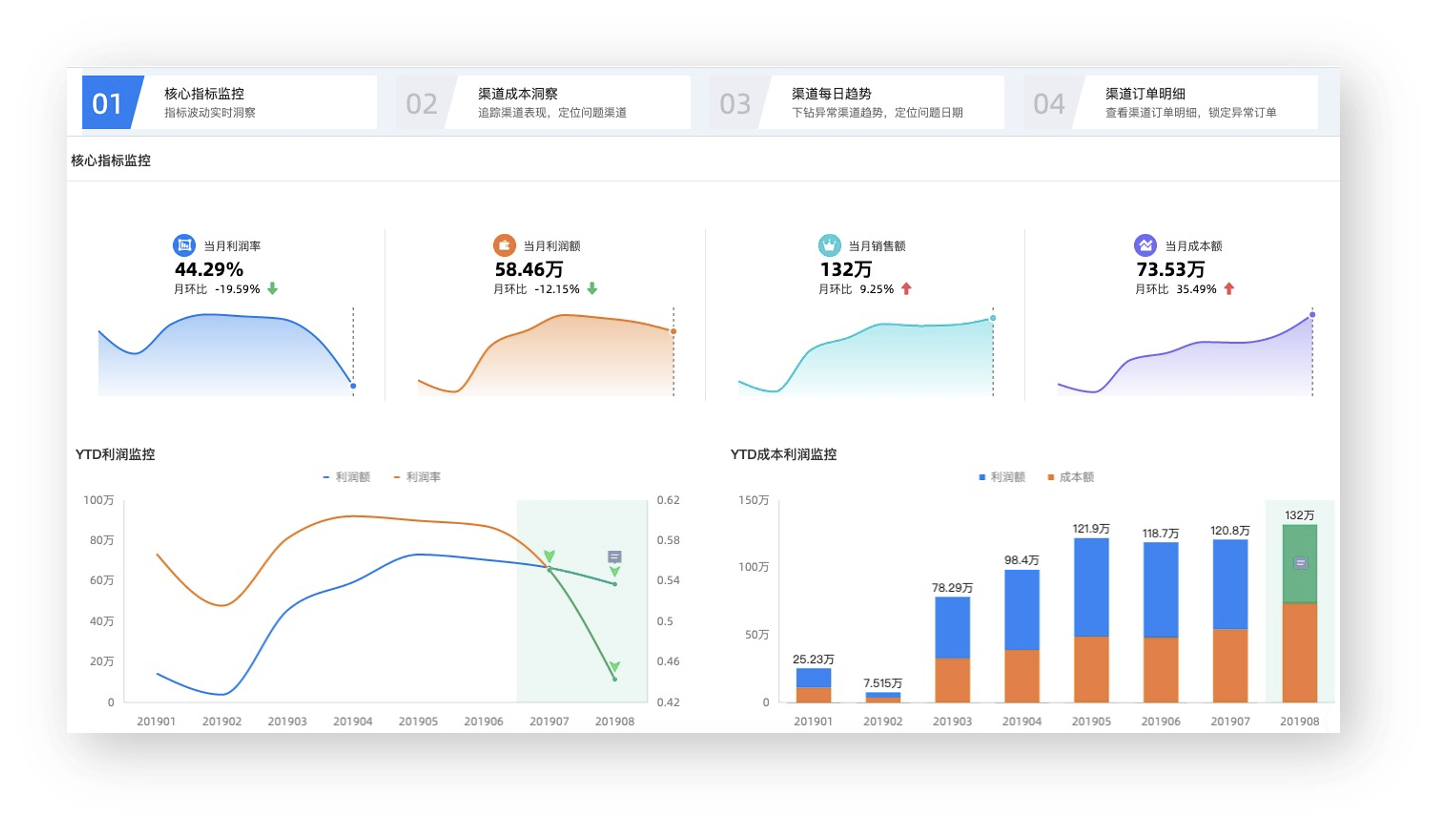
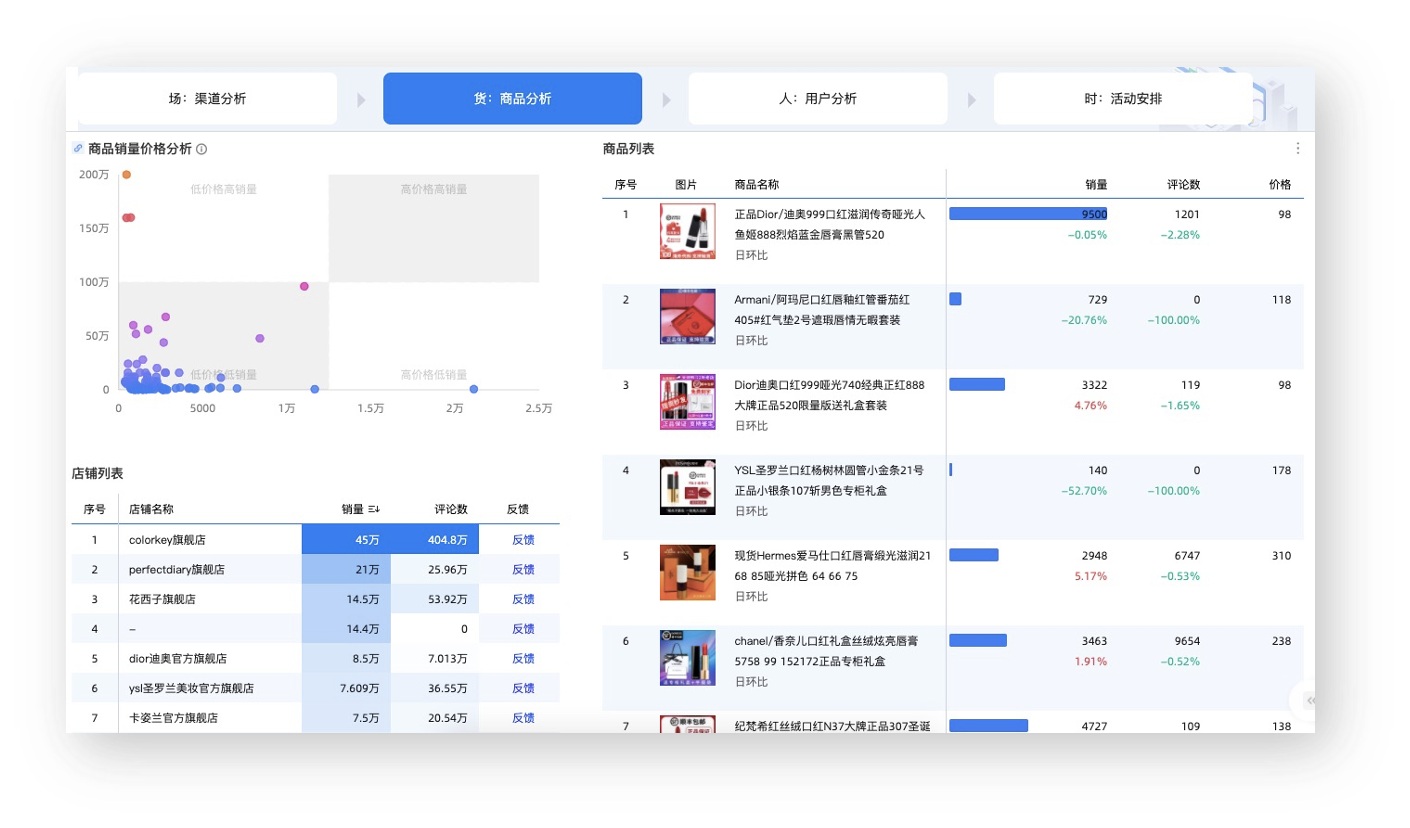
Part2 数据洞察-分析型组件

可视化一直是BI产品的核心能力，而Quick BI认为数据可视化要从简单的数据呈现向数据快速分析进行升级，而交互式的可视化可以明显提升数据分析的效率。

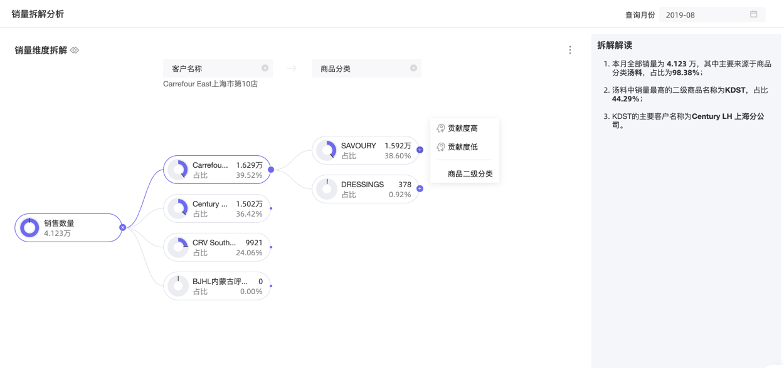
除了通过交互式的操作（钻取、联动、跳转、圈选、排除等）快速发觉数据之间的关联和组成关系，Quick BI进一步提供可交互式的图表（指标拆解图）打开全新的快速洞察方式。

新增的指标拆解图可以帮助用户自定义分析所需的指标和纬度，用户可以随时调整分析的维度和拆解顺序，在指标出现波动和异常时能够快速定位到影响原因。

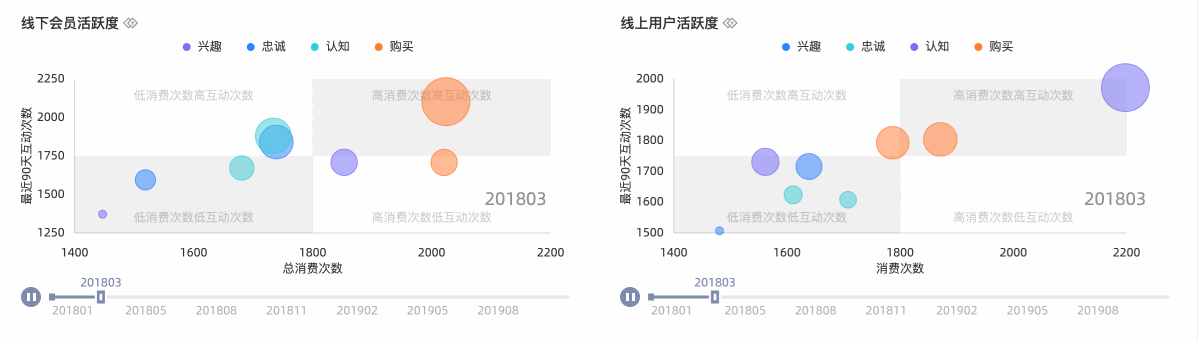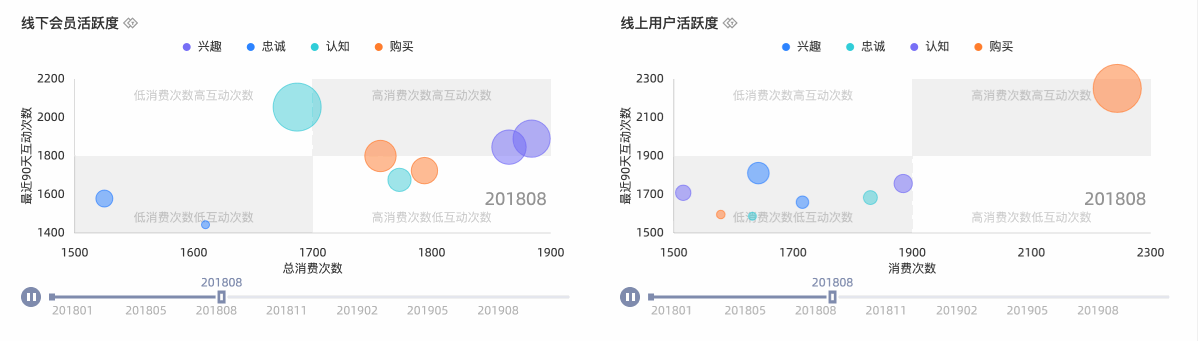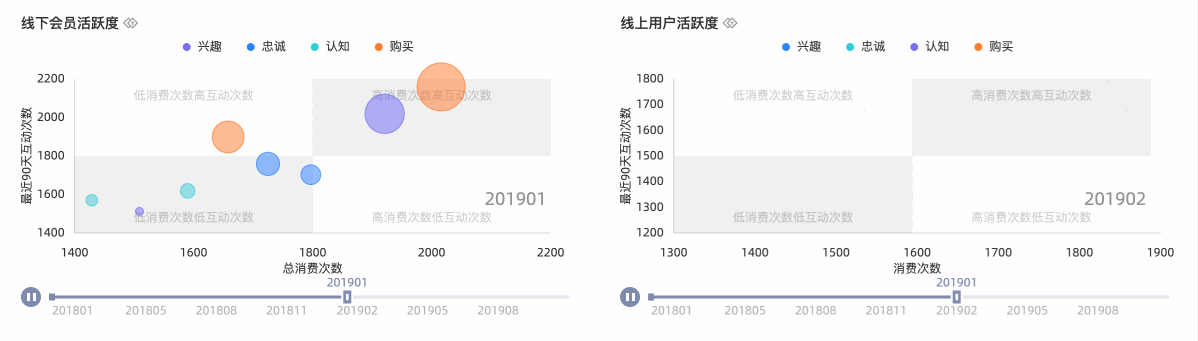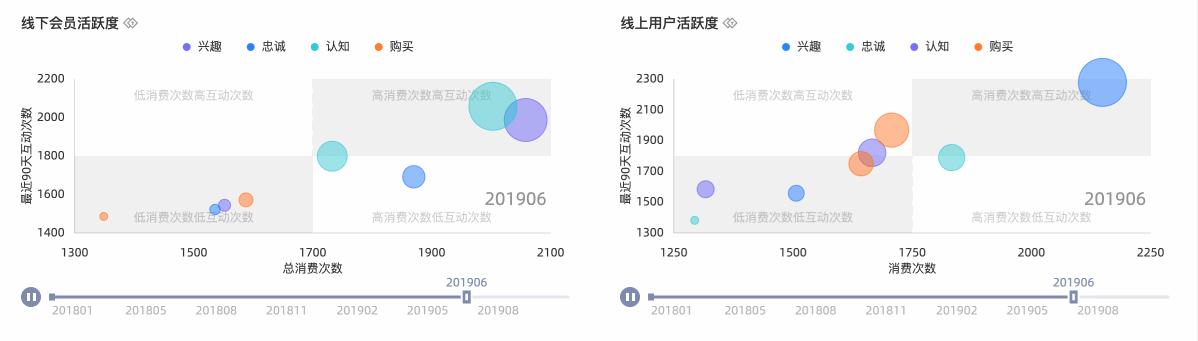
同时，Quick BI全新上线动态组件支持通过将静态的数据以动态的形式进行表达。常规的饼图、条形图、气泡图等往往只能表达切片的数据，而不能表达随时间变化而变化的数据。Quick BI通过结合播放轴和时间线可以让最普通的图形也能直观的表达出业务的动态变化。

比如今年疫情中大量使用的动态柱形图让大家一目了然的了解到各个国家和地区随时间推移的疫情变化情况。这里具体比如线下、线上的用户活跃度随时间变化的情况。

Part2 数据洞察-波动分析

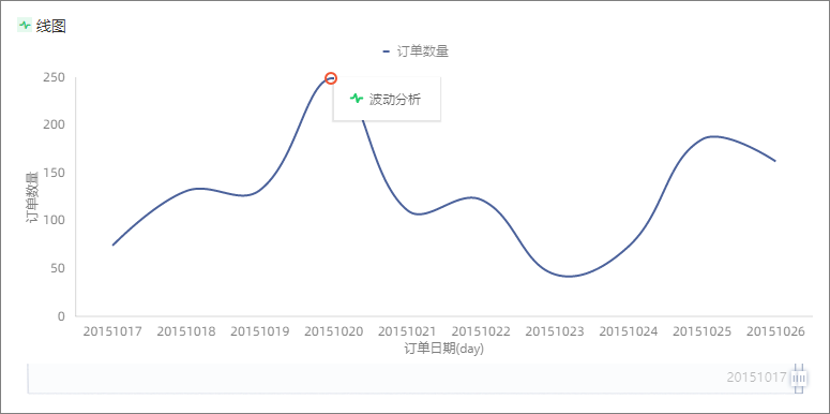
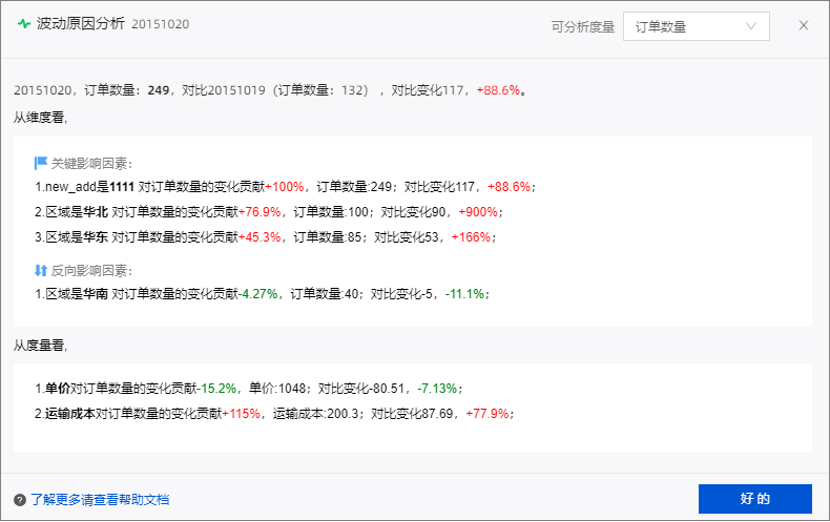
Quick BI除了能描述出数据当前的信息外，还可以通过将机器学习、人工智能和可视化分析的能力相结合，让分析人员快速获取和发现隐藏在数据中的价值。比如波动原因分析可以帮助用户在趋势类图形中自动拆解分析核心指标波动的原因，并以自然语言呈现各种因素对波动的影响情况。例如：对于某店铺订单数量的变化趋势如下，通过波动原因分析当前影响订单数量关键影响因素是 new_add是1111，以及区域为华北，可以针对性的询问一下是否进行了部分的运营活动和操作。

Part3 构建数据故事

为了解决业务中多报表且分散。以及单个报表内容量大，却没有旁人讲解时，阅览者无法读懂的问题，所以引入Data Storytelling的能力。

Data Storytelling构建数据故事是一种将交互式数据可视化与叙事技术相结合的数据表达方式，用引人注目和易于理解的形式将分析内容进行演示。Gartner近两年进一步重视Data storytelling在ABI领域的价值，Quick BI也结合自身的能力和国内用户的场景，推出了两种层次的数据故事构建能力。

第一个层次是多页面级别，Quick BI支持将大量的报表和链接组织成「数据门户」，可以帮助企业以一定的业务视角，层次递进的呈现数据分析体系。这样的门户可以是公司总体情况到分业务、分部门的形态，也可以是按照生产制造的各个环节一个一个展开数据内容。一个门户就是一个分析使用数据的视角，好的门户往往能清晰的表达企业的业务构成甚至战略方向。

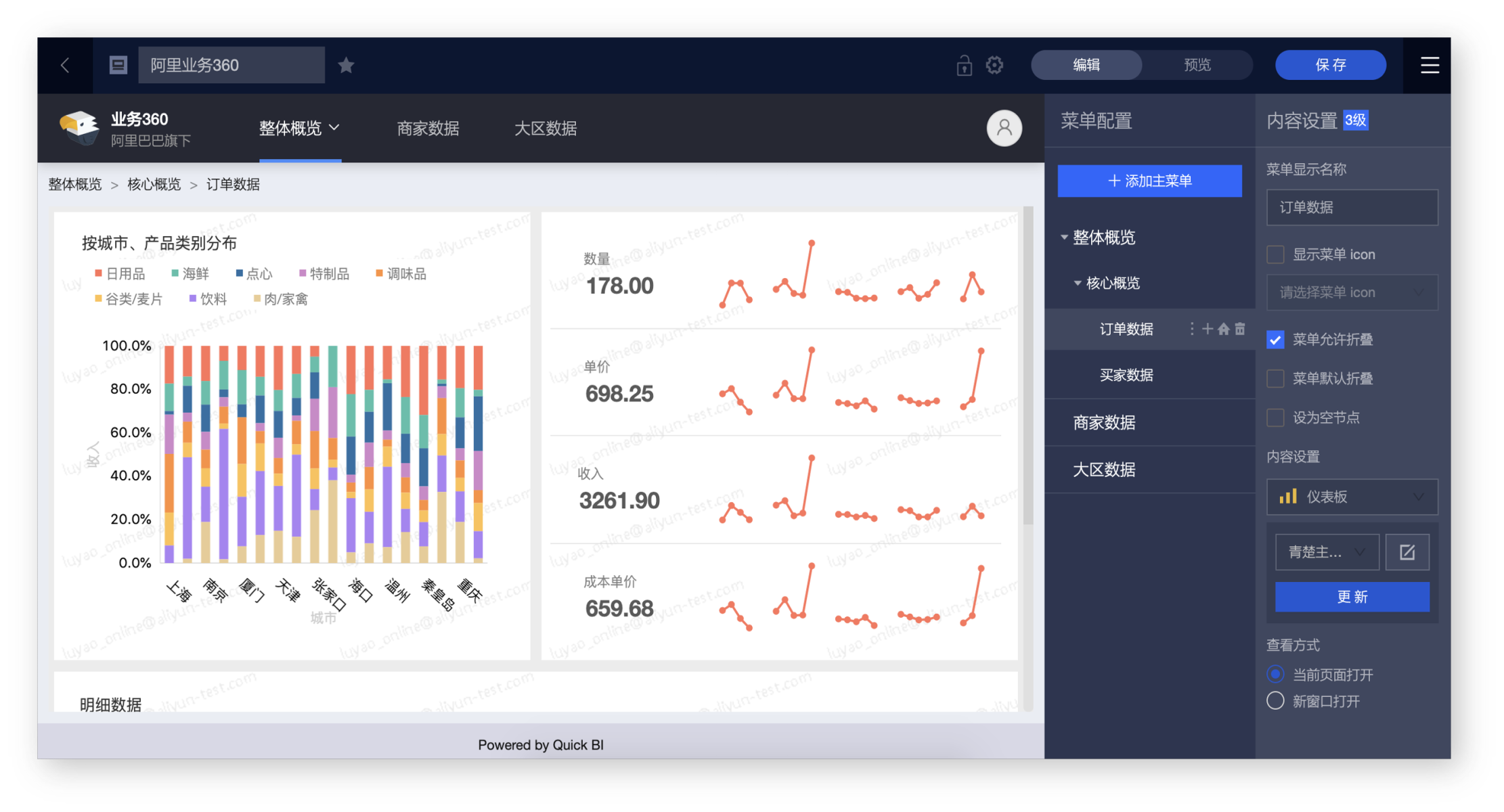
第二个层次是页面级别，单个仪表板往往聚焦于一个分析主题或几个分析指标，常以总体概览、趋势变化、不同维度切分的方式在单个页面内进行分析。而分析者经常遇到缺乏分析思路、分析组件多，不知如何选择等问题，Quick BI新引入的「故事动线」组件，可以大大提高分析师组织分析思路和呈现数据价值的效率，让报表的访问者可以快速掌握数据背后的意义和价值。

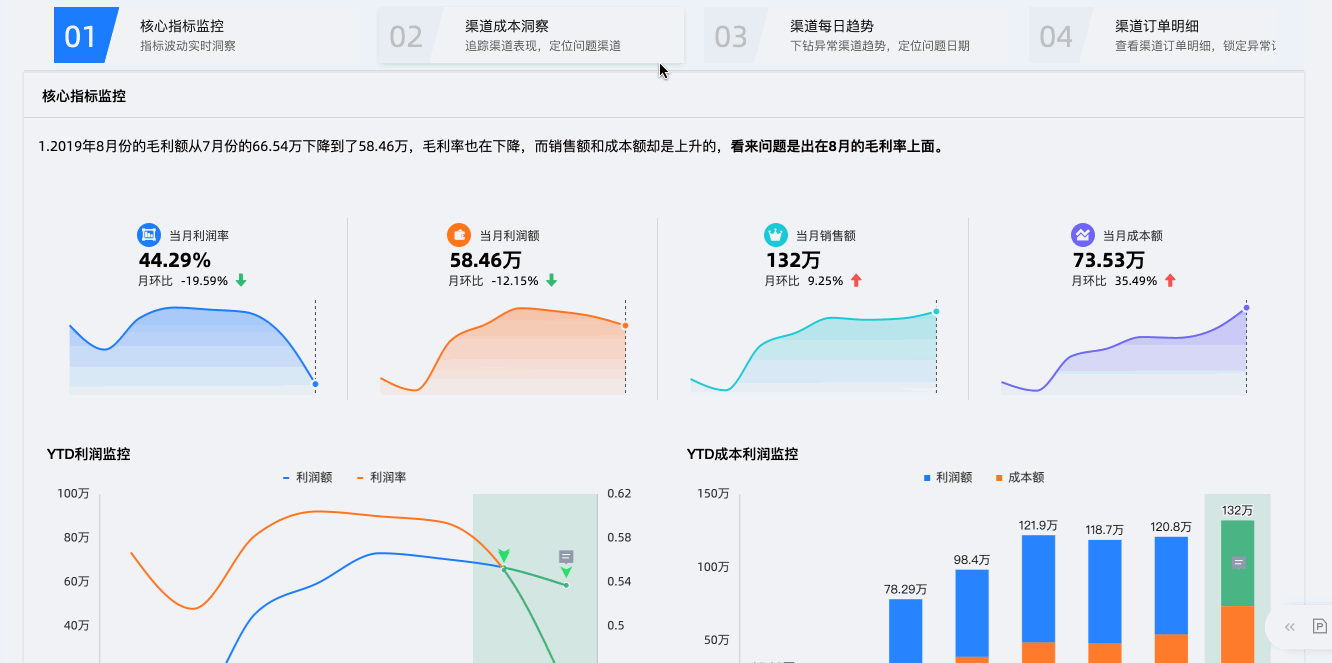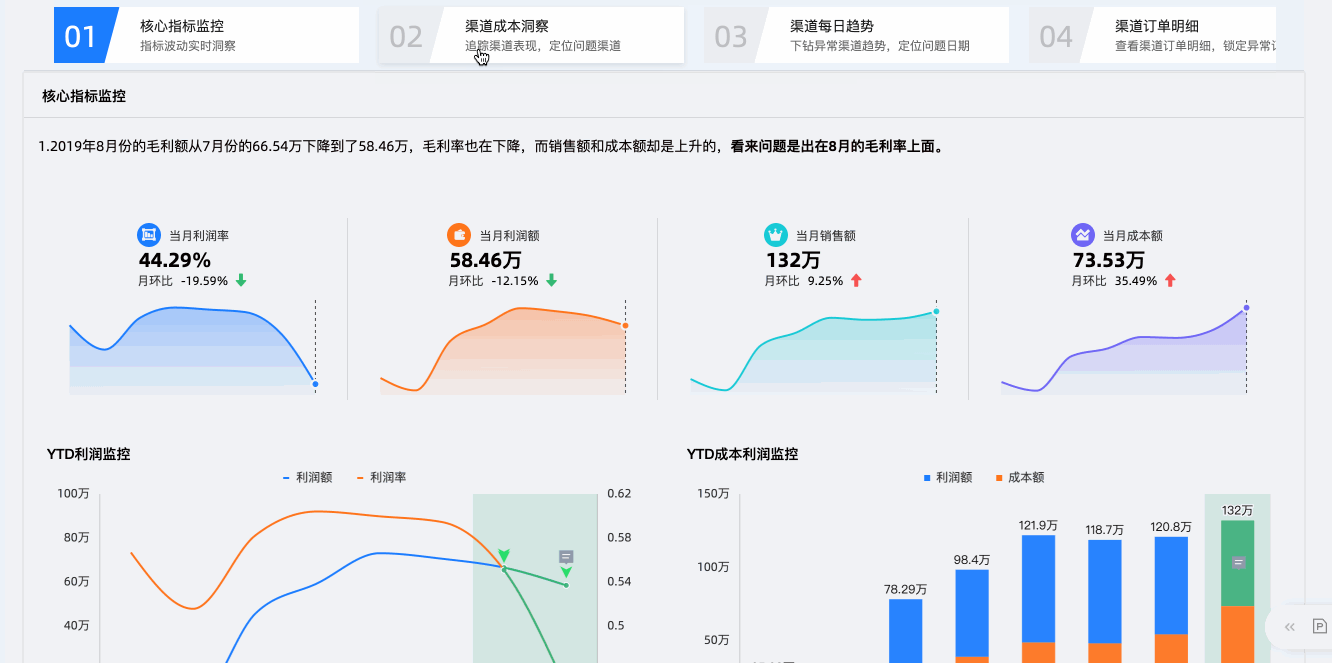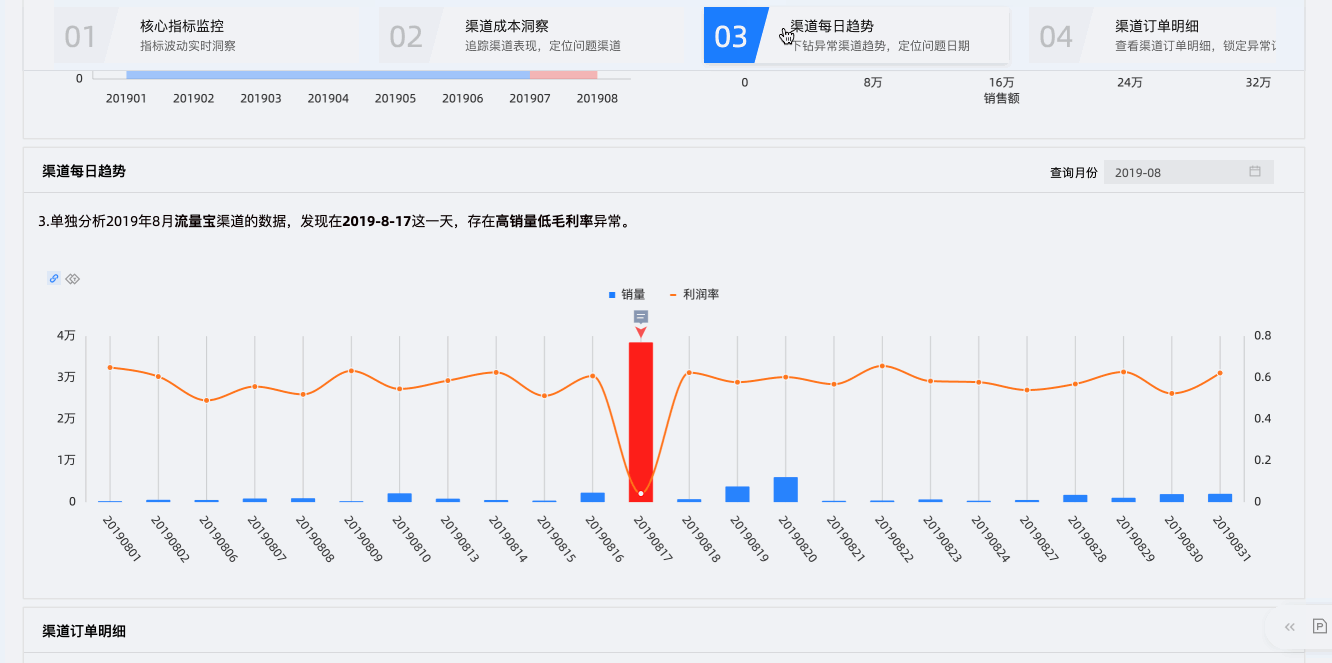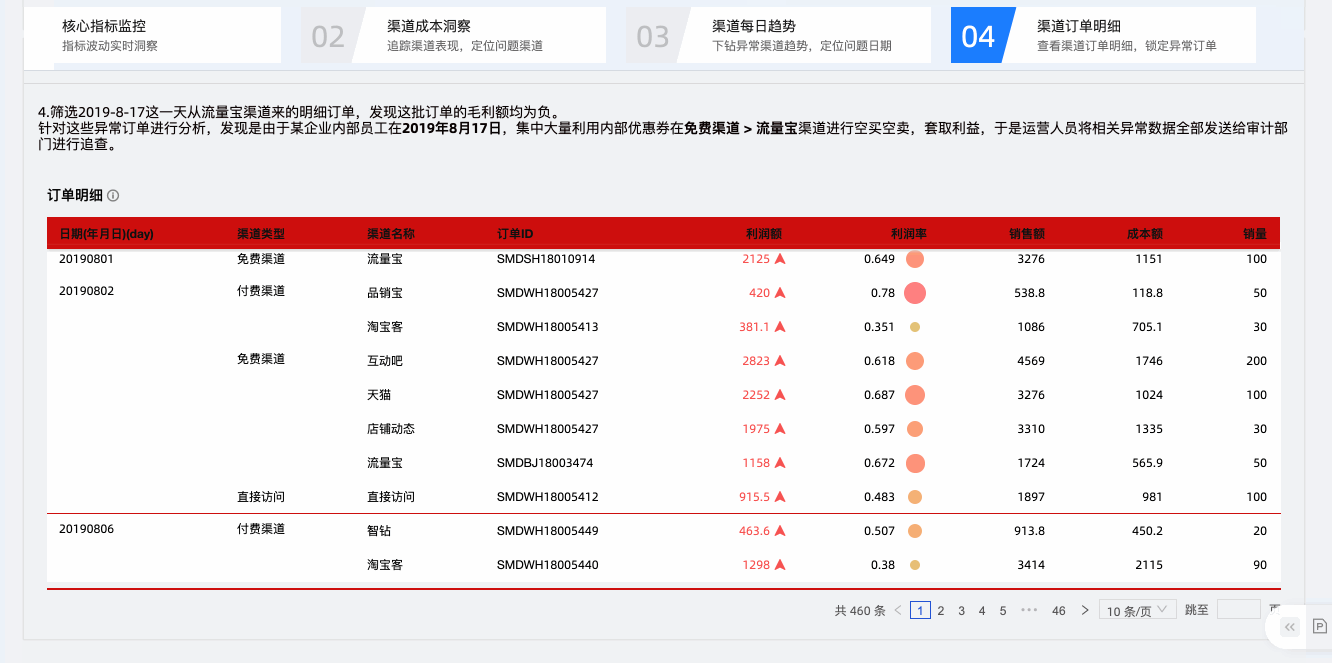
后续还会针对以上三趴分别展开说明，敬请期待！

原文链接

本文为阿里云原创内容，未经允许不得转载。