逻辑回归求解二分类问题以及SPSS的实现

分类问题就是给出物质的属性，判断其属于什么成分，本文将讲述逻辑回归求解二分类问题

本文着重于模型的实现，对于推导只是概括性的叙述

目录

• 一、问题提出
• 二、逻辑回归函数logistic
  • 1.线性线性概率模型
  • 2.sigmod函数
  • 3.求解方法————极大似然估计
  • 4.分类原则
• 三、SPSS实现————以水果二分类数据为例
  • 1.数据处理
  • 2.进行二分类逻辑回归
    • （1）输入方法
    • （2）定义分类变量
  • 3.查看结果
    • （1）块1：分类表
    • （2）逻辑回归系数表
    • （3）预测结果解读
• 四、回归结果差————如何选择合适的回归模型？
  • 1.加入平方项的实现方法
  • 2.无脑加入平方项的后果————过拟合
  • 3.如何确定合适的模型？————训练与测试

一、问题提出

二、逻辑回归函数logistic

1.线性线性概率模型

既然是回归问题，线性性是最简单的一种关系，在逻辑回归中，也是以线性概率模型作为基础进行回归。

此处的回归函数与多元线性回归一样，即y_hat=β0+β1x1+β2x2+.....

但也同样因为是2分类问题，y的值只能取0或者1。（在函数中体现为取0到1）

既然y只能取0或1那么就可以和已经非常成熟的模型————伯努利分布联系在一起，形成一个条件概率，这就是所谓的线性概率模型

2.sigmod函数

由于由于后者有解析表达式（而标准正态分布的cdf没有），所以计算logistic模型比probit模型更为方便。

3.求解方法————极大似然估计

4.分类原则

y_hat>=0.5，则认为y取1；否则认为y取0

三、SPSS实现————以水果二分类数据为例

1.数据处理

此处的数据处理部分就是把用中文表示的名词“苹果”改成数值型变量0-1，用excel容易做到，此处我们讲解用SPSS形成虚拟变量的方法



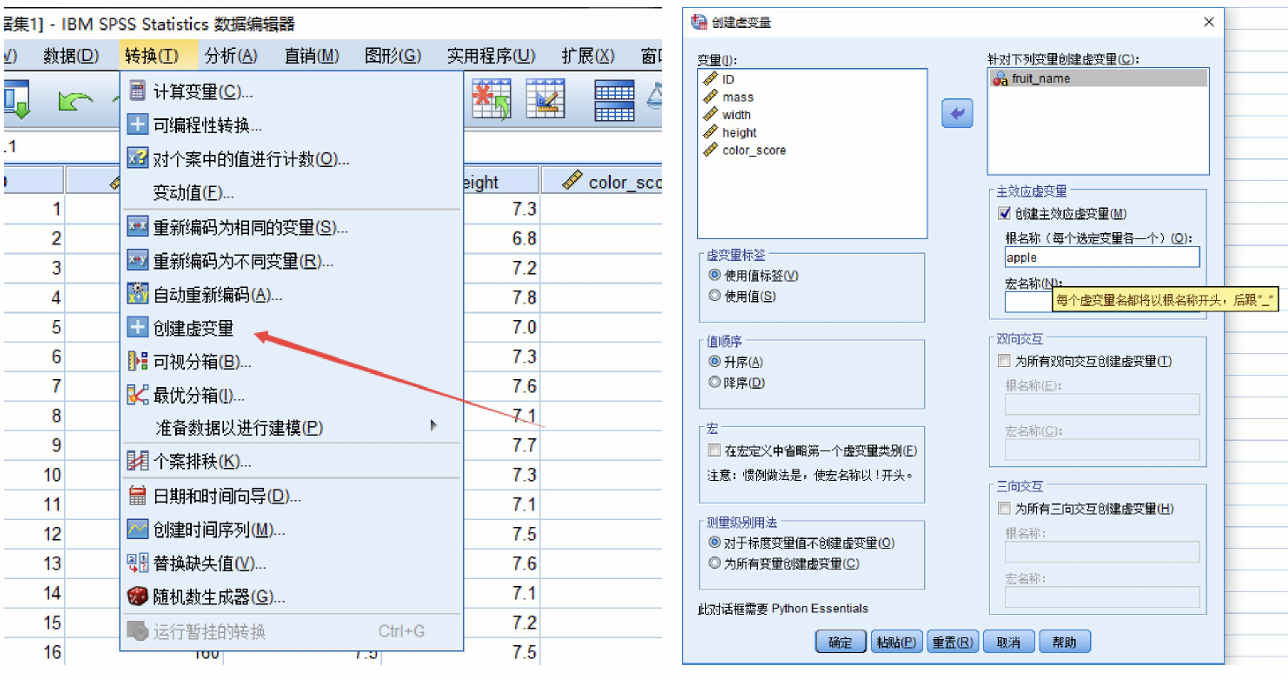
此处的“根名称”就是虚拟变量的名词，SPSS不知道哪个是0，哪个是1，于是会创造3组虚拟变量，我们只需要保留我们需要的那一组即可。此处我们保留“苹果”是1的变量

2.进行二分类逻辑回归

按图片设置好即可；需要保存概率和组成员



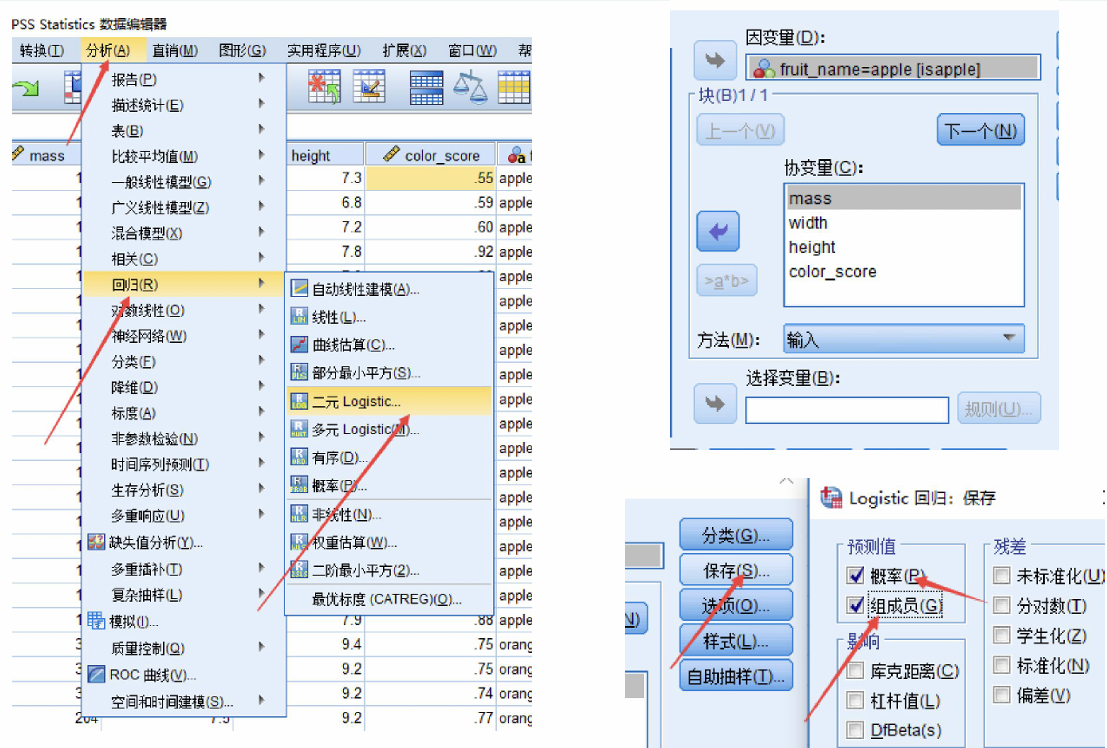
接下来我们来解释一下具体的参数调整

（1）输入方法

此处的输入方法就是指如何输入自变量的方法；

输入：把自变量全部输入

向前：先输入一个自变量，看其是否显著。如果显著则保留，不显著的去除；然后再输入另一个自变量。不同方法使用的统计量不同

向后：把自变量全部输入，观察所有的变量是否显著。把最不显著的去除，然后再次进行检验，直到把全都显著的自变量保留。不同方法使用的统计量不同

一般采用向后的方法

（2）定义分类变量

自变量是分类形式的（如性别）需要单独定义分类变量；参考类别为第一个，则把第一个设置为1。参考类别的设置对结果影响不大

3.查看结果

（1）块1：分类表

如图所示，此表是一个预测与实测数目的二元表，对角线上的个数为分类正确的个数。并且给出了分类正确率

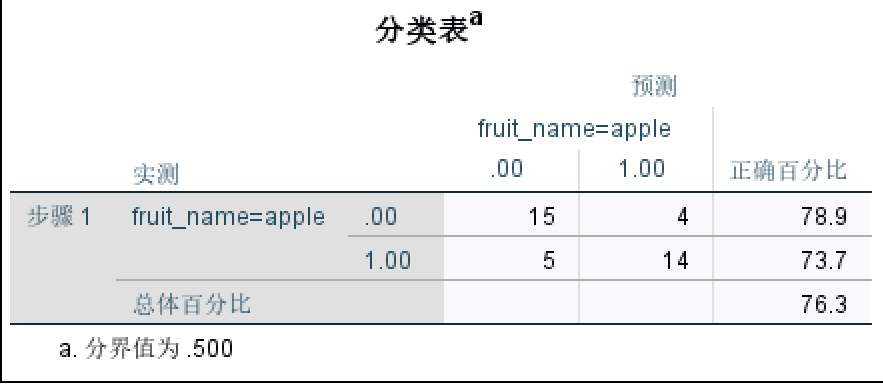
（2）逻辑回归系数表

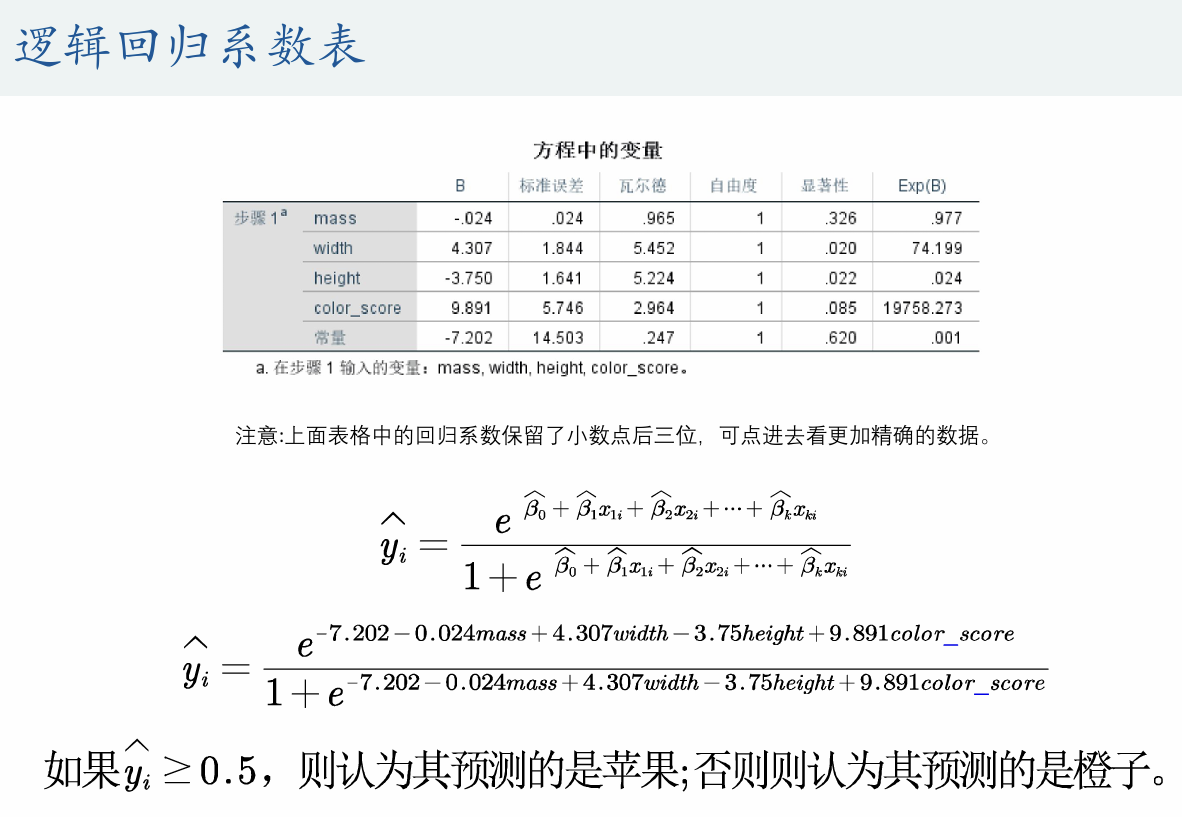
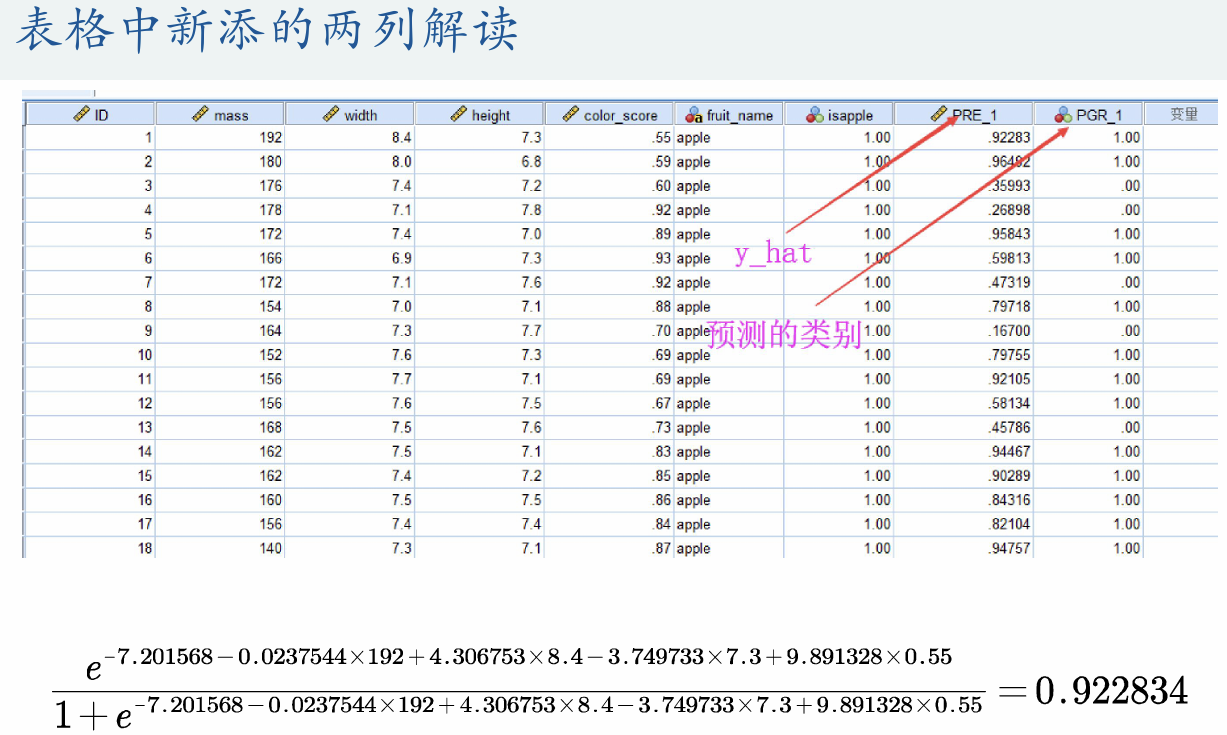
（3）预测结果解读

SPSS会在数据中给出新的两列，分别为按逻辑函数计算出来的概率值和逻辑回归后的0-1变量

四、回归结果差————如何选择合适的回归模型？

上面的方法正确率只有75%左右，显然是正确率较低的，那如何提高正确率呢？

我们的模型是以线性模型作为基础，想要提高正确率，可以提高模型的复杂度，在线性回归模型中体现为增加平方项与交互项

1.加入平方项的实现方法

在SPSS中的计算变量功能可实现

2.无脑加入平方项的后果————过拟合

在我们把所有的自变量都加入平方项后，得到结果如图所示：



可以看到，虽然预测正确率为100%，但是所有的系数都不显著了，这就导致的模型的过拟合

3.如何确定合适的模型？————训练与测试