Bike Sharing Analysis（二）- 假设检验方法

假设检验

假设检验是推论统计学（inferential statistics）的一个分支，也就是对一个较小的、有代表性的数据组（例如样本集合）进行分析与评估，并依此推断出一个大型的数据组（例如人口）的一般性结论。一个典型的例子如：估算一个国家中居民的平均身高（在这个场景下，也就是人口）。在估算时，可能会在1000个人（也就是样本）中进行分析以及评估，然后对整个国家里的居民平均身高进行估算。

假设检验尝试解决的问题：一个特定的假设值是否与直接分析（或评估）获取的值处于一致。

一般来说，假设检验的步骤如下：

1. 定义null 与 alternative hypotheses：

在第一步中，会定义一个null hypothesis（记为H₀）。这里我们定义H₀为：某国的人口平均身高为175cm。这个假设是需要之后通过统计测试进行测试的假设。Alternative hypothesis（记为H_a）由null hypothesis 的补全完整性声明组成，在这个例子中，alternative hypothesis H_a 为：平均身高不为175cm。null hypothesis 和 alternative hypothesis 永远都是相互补全的。

2. 确立合适的检验统计量：

检验统计量是基于样本计算出的一个量。它的值是决定接收或是拒绝null hypothesis 的基准。在大部分情况下，它可以由下面的公式计算得出：

这里sample statistic（样本统计值）是在样本上计算得出的统计值（在这个例子中，就是1000个样本居民的平均身高）；

value under null hypothesis（null hypothesis 下的值），假设 null hypothesis成立时的值（在这个例子中，也就是175cm）；

standard error of sample statistic（样本统计值的标准差），是样本的标准误差。

一旦test statistic 确定并计算得出后，我们需要决定它遵循什么样的概率分布。在大部分情况下，会使用如下概率分布：

1. t-分布（Student’s t-distribution），对应t-检验（t-test）
2. 标准正态分布（Standard normal）或z-分布（z-distribution），对应z-检验（z-test）
3. 卡方分布（Chi-squared distribution），对应卡方检验（chi-squared test）
4. F-分布（F-distribution），对应F-检验（F-tests）

在选择使用哪个分布时，取决于样本的大小以及检验的类别。根据经验，如果样本大小超过30，我们预期“中心极限定理的假设成立“，所以检验统计（test statistic）遵循一个标准分布（所以使用z-检验）。对于更保守的办法，或是对于小于30个样本，应使用t-检验（检验统计遵循Student’s t-分布）

3. 指定显著性水平（significance level）：

在检验统计量（test statistic）计算得出后，我们需要决定是否能拒绝null hypothesis。在执行时，我们首先指定一个显著性水平（significance level），也就是拒绝一个正确的null hypothesis 的概率。一般的方法是指定5% 的显著性水平。这个意思是：null hypothesis 为正确的，但是我们有5% 的概率拒绝它（对于更保险的方法，我们可以使用1% 或甚至0.5%）。一旦一个显著性水平被指定后，我们需要计算拒绝点（rejection points），他们是用于与检验统计量进行对比的值。如果检验统计量（test statistic）大于指定的拒绝点，则我们可以拒绝 null hypothesis 并假设 alternative hypothesis 为真。这里我们就可以将两者区分开来

4. 双侧检验（two-sided tests）：

这是在null hypothesis 假设value“等同于“一个预定义的值的时候做的检验。举个例子，全国人民的平均身高等同于175cm。在这个例子中，如果我们指定一个显著性水平为5%，则我们会有两个临界值（一正一负），它们两条尾巴的总体概率相加为5%。在计算临界值时，我们需要找到一个正态分布的两个百分比值，这两个百分比值之间的概率等同于1减去显著性水平。举个例子，如果我们假定样本的身高均值服从一个正态分布，指定检验的显著性水平为5%，则我们需要找到两个百分比数，落入它们区间之外的值的概率等于0.05。由于它的概率由两条尾巴进行分割，所以这2个百分数就是2.5 和 97.5。对于一个正态分布来说，对应的值就是-1.96 和 1.96，这就是两个临界值。所以，如果以下为真，则我们不会拒绝null hypothesis：

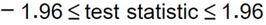
如果上面的公式不为真，那也就是说，检验统计值（test statistic）大于1.96或是小于-1.96，则我们拒绝null hypothesis

5. 单侧检验（One-sided tests）：

这是在null hypothesis 假定value “大于“或是”小于“一个预定义值的时候做的检验。例如，全国人民的平均身高高于175cm。在这个例子中，如果我们指定一个显著性水平为5%，则我们将仅有一个临界值，它的尾巴的概率等同于5%。在找这个临界值时，我们需要找到一个正态分布的一个百分数，对应的是尾部概率等于0.05 的值。对于”大于“类型的检验，临界值对应于5-分位数，或是-1.645（若是检验遵从一个正态分布）；对于”小于“类型的检验，临界值对应为95-分位数，或是1.645。所以，若是以下为真，则我们会拒绝null hypothesis（”大于“检验的情况）：

反之，对于“小于“检验的类型，若是以下公式为真，则我们拒绝null hypothesis：

需要注意的是，通常情况下，相对于计算一个特定显著性水平的临界值，我们会使用检验的 p 值（p-value）。p值是在null hypothesis可以被拒绝时的最小显著性水平。p 值也提供了，在null hypothesis 为真的情况下，获取观测到的样本统计量的概率。如果获取的 p 值小于一个指定的显著性水平，则我们可以拒绝null hypothesis。所以p值的方法，在实际使用中，是另一个（大多数情况下也是更方便的一个）执行假设检验的方法。

下一章我们会使用 Python 来演示一个实际执行假设检验的例子。