RSA非对称加密算法中的密钥对生成与传输

PrimiHub一款由密码学专家团队打造的开源隐私计算平台，专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。

RSA（Rivest–Shamir–Adleman）加密算法是一种基于大素数分解难题的非对称加密算法，由Ron Rivest、Adi Shamir和Leonard Adleman于1977年提出。RSA算法广泛应用于数字签名、数据加密和密钥交换等领域，其安全性依赖于两个大素数的乘积难以分解的特性。RSA算法的核心是利用一对密钥：公钥和私钥。本文将详细介绍RSA算法中的密钥对生成与传输过程，并分析其在实际应用中的重要性和方法。

RSA算法简介

基本原理

RSA算法的安全性依赖于大整数分解的计算复杂性。具体来说，RSA算法基于以下几个基本数学原理：

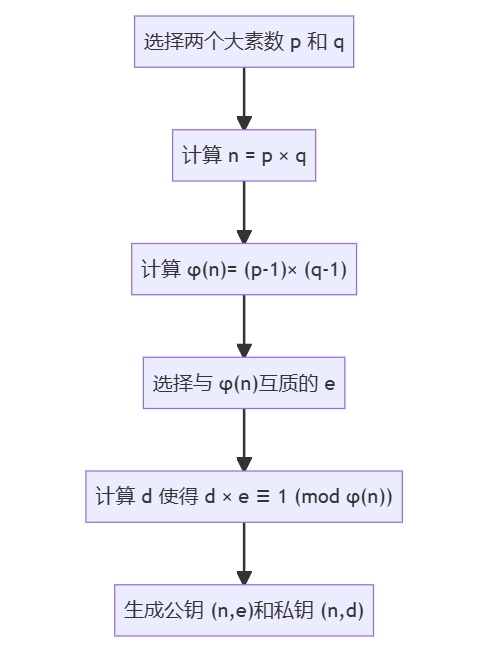
素数选择：选择两个大素数 $p$ 和 $q$。
模数计算：计算模数 $n$，其中 $n = p \times q$。
欧拉函数：计算欧拉函数 $\phi(n)$，其中 $\phi(n) = (p-1) \times (q-1)$。
公钥指数选择：选择一个小于 $\phi(n)$ 且与 $\phi(n)$ 互质的整数 $e$。
私钥指数计算：计算私钥指数 $d$，使得 $d \times e \equiv 1 \ (\text{mod} \ \phi(n))$。

公钥由 $(n, e)$ 组成，私钥由 $(n, d)$ 组成。

数学公式

RSA算法的加密和解密过程可以通过以下公式表示：

加密：给定明文 $m$ 和公钥 $(n, e)$，密文 $c$ 通过公式 $c = m^e \ (\text{mod} \ n)$ 生成。
解密：给定密文 $c$ 和私钥 $(n, d)$，明文 $m$ 通过公式 $m = c^d \ (\text{mod} \ n)$ 还原。

流程图示

密钥生成主体

用户自身生成

用户在本地设备上生成密钥对的优点是私钥始终不离开用户设备，安全性高。然而，如果用户设备被攻破，私钥可能被窃取。

可信第三方生成

由可信的第三方（如认证机构）生成并分发密钥对可以简化用户操作。这种方式需要信任第三方不会滥用或泄露私钥。通常，可信第三方会采用严格的安全措施和审计机制来保护密钥。

硬件安全模块（HSM）生成

硬件安全模块（HSM）是一种专用设备，设计用于高安全性环境中生成、存储和管理密钥。HSM具有防篡改和防物理攻击的特点，可以显著提高密钥的安全性。

云端密钥管理服务

近年来，随着云计算的发展，许多云服务提供商（如AWS、Azure、Google Cloud）提供了云端密钥管理服务（KMS）。用户可以利用KMS在云端生成和管理RSA密钥对，这种方式不仅方便快捷，还具备一定的安全性和可扩展性。

密钥传输

公钥传输

公钥传输不需要保密，但必须确保其完整性和真实性。常见的公钥传输方式包括：

公开发布

用户可以将公钥发布在公开场所，如公司网站、社交媒体平台或公告栏。这种方式简单直观，但需防止恶意篡改。

数字证书

数字证书是一种电子文档，由权威认证机构（CA）签发，包含持有者身份信息和公钥。数字证书可以确保公钥的真实性，并防止中间人攻击。数字证书通常采用X.509标准格式，广泛应用于SSL/TLS协议中。

可信中介传输

通过可信中介（如邮件、消息传递服务）传输公钥时，需确保中介本身的安全性。例如，可以通过加密的电子邮件或受信任的消息应用（如Signal、WhatsApp）发送公钥。

私钥传输

私钥传输必须保证其保密性和完整性，常见的传输方式包括：

物理传输

将私钥存储在安全介质（如U盘、智能卡）中，通过安全渠道（如专人送达）传输。这种方式适用于需要极高安全性的场合，但成本较高。

加密传输

使用对称加密算法加密私钥，通过安全通信渠道（如SSL/TLS）传输。加密传输可以在一定程度上保证私钥的安全性，但前提是对称密钥的管理同样需要高安全措施。

密钥分割技术

将私钥分割成多个部分，分别通过不同渠道传输，接收方在接收到所有部分后再进行合并。这种方式可以提高私钥传输的安全性，防止单一渠道被攻破。

密钥管理与保护

无论使用何种方式传输密钥，密钥管理与保护都是至关重要的。以下是一些关键的密钥管理与保护措施：

密钥备份与恢复

定期备份密钥并确保备份的安全存储，可以防止因设备故障或数据丢失导致密钥丢失。同时，制定密钥恢复策略，确保在紧急情况下能够迅速恢复密钥。

密钥轮换

定期轮换密钥可以降低密钥被破解或泄露的风险。密钥轮换应遵循一定的策略，如每隔一段时间或在发现安全事件后立即进行轮换。

密钥销毁

当密钥不再需要时，应及时销毁。密钥销毁应采用安全的方法，确保密钥无法被恢复或重建。

实际应用中的密钥生成与传输

为了更好地理解RSA密钥对生成与传输的实际应用，我们以一个具体的案例来说明。

案例分析：Alice与Bob的通信

假设Alice希望与Bob进行安全的通信，他们可以采用以下步骤来生成和传输RSA密钥对：

密钥生成：
- Alice在本地生成RSA密钥对，得到公钥 $(n_A, e_A)$ 和私钥 $(n_A, d_A)$。
- Bob同样在本地生成RSA密钥对，得到公钥 $(n_B, e_B)$ 和私钥 $(n_B, d_B)$。
公钥交换：
- Alice将她的公钥 $(n_A, e_A)$ 发送给Bob，确保公钥传输的安全性和完整性。
- Bob收到Alice的公钥后，也将自己的公钥 $(n_B, e_B)$ 发送给Alice。
私钥保护：
- Alice和Bob都严格保护自己的私钥 $d_A$ 和 $d_B$，确保只有授权的人能够访问私钥。
- 私钥可以存储在安全的硬件设备或使用加密算法加密后存储。
安全通信：
- Alice使用Bob的公钥 $(n_B, e_B)$ 加密要发送给Bob的消息。
- Bob收到密文后，使用自己的私钥 $d_B$ 解密消息。

通过这种方式，Alice和Bob可以安全地进行加密通信，保护其消息免受窥探和篡改。

RSA非对称加密算法的密钥对生成与传输是信息安全领域的核心问题之一。密钥生成过程需要保证随机性和安全性，而密钥的传输则需要选择适当的方式来确保其保密性和完整性。通过合理的密钥管理和保护措施，可以有效地利用RSA算法保护通信安全，防止信息泄露和篡改。在实际应用中，用户和系统管理员需要结合具体情况选择最佳的密钥生成和传输策略，以达到最佳的安全性和效率。

PrimiHub一款由密码学专家团队打造的开源隐私计算平台，专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。