二叉树的遍历（BFS、DFS）

本文分为以下部分：

先序遍历
中序遍历
后序遍历

BFS（广度优先搜索）

广度优先搜索[^1]（英语：Breadth-First Search，缩写为BFS），又译作宽度优先搜索，或横向优先搜索，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。广度优先搜索的实现一般采用open-closed表。

先遍历每层的节点，优先对相邻节点做相同操作，再对下一层进行操作，直到所有操作完成。

简单来说就是一层一层的进行操作，横向操作。

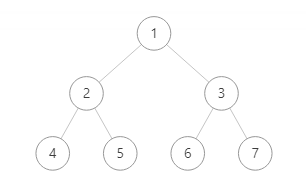
例如上图，用广度优先搜索算法将节点值输出，则输出结果为 1 2 3 4 5 6 7

第一层输出 1 ，然后输出第二层 2 3 ，最后输出第三层 4 5 6 7

实现方法：

（队列先进先出原则）

首先定义一个单端队列，将根节点加入队列中
判断队列是否为空，不为空则取出队列的第一个节点，输出节点的值，将节点的左、右节点加入队列中
重复第二步，直到队列为空

e.g.

定义一个单端队列queue，将根节点 1 加入队列中
从队列中取出节点 1 ，输出节点的的值 1 ，将节点 2 、3 加入队列中
由于队列先进先出特性，所以取出节点 2 ，输出节点值 2 ，将节点 4 、5 加入队列
此时取出的是节点 3，输出节点值 3 ，将节点 6 、7 加入队列
......

最终输出为 1 2 3 4 5 6 7

public class ErgodicTree {

    @Test

    public void test(){

        Node root = new Node(1);

        Node node = new Node(2);

        Node node1 = new Node(3);

        Node node2 = new Node(4);

        Node node3 = new Node(5);

        Node node4 = new Node(6);

        Node node5 = new Node(7);

        root.setLeft(node);

        root.setRight(node1);

        node.setLeft(node2);

        node.setRight(node3);

        node1.setLeft(node4);

        node1.setRight(node5);

        this.bfs(root);

    }

    //广度优先搜索

    //1 => 2 => 3 => 4 => 5 => 6 => 7 =>

    public void bfs(Node node){

        Queue<Node> queue = new LinkedList<Node>();

        //将根节点加入队列中

        queue.offer(node);

        while (!queue.isEmpty()){

            //获取队列的第一个节点

            Node poll = queue.poll();

            if(poll != null){

                //输出获取到的节点值

                System.out.print(poll.getValue() + " => ");

                //将该节点的左侧节点加入队列中

                queue.offer(poll.getLeft());

                //将该节点的右侧节点加入队列中

                queue.offer(poll.getRight());

            }

        }

    }

}

//节点定义

class Node{

    private int value;

    private Node left;

    private Node right;

    public Node(int value) {

        this.value = value;

    }

    public int getValue() {

        return value;

    }

    public Node getLeft() {

        return left;

    }

    public void setLeft(Node left) {

        this.left = left;

    }

    public Node getRight() {

        return right;

    }

    public void setRight(Node right) {

        this.right = right;

    }

}

DFS（深度优先搜索）

深度优先搜索算法[^1]（英语：Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

遍历一列的节点，再对下一列的节点进行操作，直到所有操作完成

简单来说就是一列一列的进行操作，纵向操作。

先序遍历

（先）根左右

每次遍历都先根，再遍历左子树，再遍历右子树，依旧以上图为例

先根节点，输出 1

再遍历左子树，左子树为 2 4 5

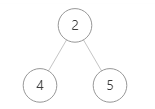
遍历左子树的根节点，输出 2

再遍历左子树，左子树为单独的 4 ，所以输出 4

2 的左子树遍历完，再遍历 2 的右子树，右子树为单独的 5 ，所以输出 5

1 的左子树遍历完，回溯遍历 1 的右子树，右子树为 3 6 7

遍历右子树依旧为先 根左右 ，根为 3 ，输出 3

再遍历左子树，左子树为单独的6，所以输出 6

3 的左子树遍历完，再遍历 3 的右子树，右子树为单独的 7 ，所以输出 7

整个树遍历完了，所以最终输出的是 1 2 4 5 3 6 7

代码实现

public class ErgodicTree {

    @Test

    public void test(){

        Node root = new Node(1);

        Node node = new Node(2);

        Node node1 = new Node(3);

        Node node2 = new Node(4);

        Node node3 = new Node(5);

        Node node4 = new Node(6);

        Node node5 = new Node(7);

        root.setLeft(node);

        root.setRight(node1);

        node.setLeft(node2);

        node.setRight(node3);

        node1.setLeft(node4);

        node1.setRight(node5);

        this.preOrder(root);

    }

    //先序遍历

    //1 => 2 => 4 => 5 => 3 => 6 => 7 =>

    public void preOrder(Node node){

        if(node != null){

            //输出当前节点

            System.out.print(node.getValue() + " => ");

            //遍历左子树

            preOrder(node.getLeft());

            //遍历右子树

            preOrder(node.getRight());

        }

    }

}

class Node{

    private int value;

    private Node left;

    private Node right;

    public Node(int value) {

        this.value = value;

    }

    public int getValue() {

        return value;

    }

    public Node getLeft() {

        return left;

    }

    public void setLeft(Node left) {

        this.left = left;

    }

    public Node getRight() {

        return right;

    }

    public void setRight(Node right) {

        this.right = right;

    }

}

中序遍历

（中）根左右，即左根右

先序遍历是先根左右，中序遍历是中根左右，即左根右，左子树，根节点，再右子树，以最开始的图为例

先遍历根节点 1 的左子树 2 4 5

由于节点 2 还有左子树，所以先遍历 2 的左子树

左子树为单独的 4 ，4 没有左子树（若存在左子树，则需要继续往下递推），所以输出 4

2 的左子树遍历完，输出 2 的根节点自己，输出 2

2 的右子树依旧为 1 的左子树的部分，所以先遍历 2 的右子树
2右子树为单独的 5，5 没有左子树，所以输出 5

1 的左子树都遍历完了，该遍历 1 的根节点了，输出 1

再遍历 1 的右子树 3 6 7，右子树的遍历依旧遵循左根右

由于节点 3 还有左子树，所以先遍历 3 的左子树

左子树为单独的 6 ，6 没有他左子树，所以输出 6

3 的左子树遍历完，输出 3 的根节点自己，输出 3
接着遍历 3 的右子树

右子树为单独的 7，7 没有左子树，所以输出 7

最终输出为 4 2 5 1 6 3 7

代码实现

public class ErgodicTree {

    @Test

    public void test(){

        Node root = new Node(1);

        Node node = new Node(2);

        Node node1 = new Node(3);

        Node node2 = new Node(4);

        Node node3 = new Node(5);

        Node node4 = new Node(6);

        Node node5 = new Node(7);

        root.setLeft(node);

        root.setRight(node1);

        node.setLeft(node2);

        node.setRight(node3);

        node1.setLeft(node4);

        node1.setRight(node5);

        this.midOrder(root);

    }

    //中序遍历

    //4 => 2 => 5 => 1 => 6 => 3 => 7 =>

    public void midOrder(Node node){

        if(node != null){

        	//先遍历左子树

            midOrder(node.getLeft());

            //输出当前节点

            System.out.print(node.getValue() + " => ");

            //遍历右子树

            midOrder(node.getRight());

        }

    }

}

class Node{

    private int value;

    private Node left;

    private Node right;

    public Node(int value) {

        this.value = value;

    }

    public int getValue() {

        return value;

    }

    public Node getLeft() {

        return left;

    }

    public void setLeft(Node left) {

        this.left = left;

    }

    public Node getRight() {

        return right;

    }

    public void setRight(Node right) {

        this.right = right;

    }

}

后序遍历

（后）根左右，即左右根

后序遍历就是根在最后遍历，顺序为左右根，即左子树，右子树，根节点，依旧以最初的图为例

先遍历根节点 1 的左子树 2 4 5

由于节点 2 还有左子树，所以先遍历 2 的左子树

左子树为单独的 4 ，4 没有左子树，也没有右子树（若存在左/右子树，则需要继续往下递推），所以输出 4

遍历完 2 的左子树，再遍历 2 的右子树
右子树为单独的 5 ，5 没有左子树，也没有右子树，所以输出 5

最后遍历 2 自己，输出 2

再遍历根节点 1 的右子树

由于节点 3 还有左子树，所以先遍历 3 的左子树

左子树为单独的 6 ，6 没有左子树，也没有右子树，所以输出 6

遍历完 3 的左子树，再遍历 3 的右子树
左子树为单独的 7 ，7 没有左子树，也没有右子树，所以输出 7

最后遍历 3 自己，输出 3

最后遍历根节点 1 ，输出 1

最后的输出结果为 4 5 2 6 7 3 1

代码实现

public class ErgodicTree {

    @Test

    public void test(){

        Node root = new Node(1);

        Node node = new Node(2);

        Node node1 = new Node(3);

        Node node2 = new Node(4);

        Node node3 = new Node(5);

        Node node4 = new Node(6);

        Node node5 = new Node(7);

        root.setLeft(node);

        root.setRight(node1);

        node.setLeft(node2);

        node.setRight(node3);

        node1.setLeft(node4);

        node1.setRight(node5);

        this.postOrder(root);

    }

    //后序遍历

    //4 => 5 => 2 => 6 => 7 => 3 => 1 =>

    public void postOrder(Node node){

        if(node != null){

            postOrder(node.getLeft());

            postOrder(node.getRight());

            System.out.print(node.getValue() + " => ");

        }

    }

}

class Node{

    private int value;

    private Node left;

    private Node right;

    public Node(int value) {

        this.value = value;

    }

    public int getValue() {

        return value;

    }

    public Node getLeft() {

        return left;

    }

    public void setLeft(Node left) {

        this.left = left;

    }

    public Node getRight() {

        return right;

    }

    public void setRight(Node right) {

        this.right = right;

    }

}

总结

BFS : 不用递归，使用队列来进行遍历操作。
DFS : 通常使用递归，三种遍历方式从代码上看就只是输出的位置的替换。

各有各的优点，不同问题不同分析。

参考文献

[^1]: 维基百科