poj 1279 半平面交核面积
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6668 | Accepted: 2725 |
Description
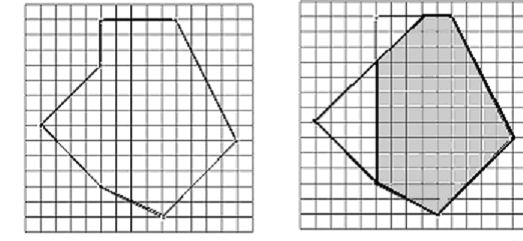
Input
Output
Sample Input
1
7
0 0
4 4
4 7
9 7
13 -1
8 -6
4 -4
Sample Output
80.00
/*
poj 1279 半平面交核面积 给你一个多边形的图书馆.要求得到一块地方能看见墙上所有的点,并求出面积
在半平面模板上加个求面积公式即可.
而且输入并没有指定顺时针还是逆时针,可以通过求面积进行判断. hhh-2016-05-11 21:01:47
*/
#include <iostream>
#include <vector>
#include <cstring>
#include <string>
#include <cstdio>
#include <queue>
#include <cmath>
#include <algorithm>
#include <functional>
#include <map>
using namespace std;
#define lson (i<<1)
#define rson ((i<<1)|1)
typedef long long ll;
using namespace std;
const int maxn = 1510;
const double PI = 3.1415926;
const double eps = 1e-8; int sgn(double x)
{
if(fabs(x) < eps) return 0;
if(x < 0)
return -1;
else
return 1;
} struct Point
{
double x,y;
Point() {}
Point(double _x,double _y)
{
x = _x,y = _y;
}
Point operator -(const Point &b)const
{
return Point(x-b.x,y-b.y);
}
double operator ^(const Point &b)const
{
return x*b.y-y*b.x;
}
double operator *(const Point &b)const
{
return x*b.x + y*b.y;
}
}; struct Line
{
Point s,t;
double k;
Line() {}
Line(Point _s,Point _t)
{
s = _s;
t = _t;
k = atan2(t.y-s.y,t.x-s.x);
}
Point operator &(const Line &b) const
{
Point res = s;
double ta = ((s-b.s)^(b.s-b.t))/((s-t)^(b.s-b.t));
res.x += (t.x-s.x)*ta;
res.y += (t.y-s.y)*ta;
return res;
}
}; bool HPIcmp(Line a,Line b)
{
if(fabs(a.k-b.k) > eps) return a.k<b.k;
return ((a.s-b.s)^(b.t-b.s)) < 0;
}
Line li[maxn]; double CalArea(Point p[],int n)
{
double ans = 0;
for(int i = 0;i < n;i++)
{
ans += (p[i]^p[(i+1)%n])/2;
}
return ans;
} double HPI(Line line[],int n,Point res[],int &resn)
{
int tot =n;
sort(line,line+n,HPIcmp);
tot = 1;
for(int i = 1; i < n; i++)
{
if(fabs(line[i].k - line[i-1].k) > eps)
line[tot++] = line[i];
}
int head = 0,tail = 1;
li[0] = line[0];
li[1] = line[1];
resn = 0;
for(int i = 2; i < tot; i++)
{
if(fabs((li[tail].t-li[tail].s)^(li[tail-1].t-li[tail-1].s)) < eps||
fabs((li[head].t-li[head].s)^(li[head+1].t-li[head+1].s)) < eps)
return 0;
while(head < tail && (((li[tail] & li[tail-1]) - line[i].s) ^ (line[i].t-line[i].s)) > eps)
tail--;
while(head < tail && (((li[head] & li[head+1]) - line[i].s) ^ (line[i].t-line[i].s)) > eps)
head++;
li[++tail] = line[i];
}
while(head < tail && (((li[tail] & li[tail-1]) - li[head].s) ^ (li[head].t-li[head].s)) > eps)
tail--;
while(head < tail && (((li[head] & li[head-1]) - li[tail].s) ^ (li[tail].t-li[tail].t)) > eps)
head++;
if(tail <= head+1)
return 0;
for(int i = head; i < tail; i++)
res[resn++] = li[i]&li[i+1];
if(head < tail-1)
res[resn++] = li[head]&li[tail]; double tans = 0;
for(int i = 0;i < resn;i++)
{
tans += (res[i]^res[(i+1)%resn])/2;
}
return fabs(tans);
}
Point p0;
Point lis[maxn];
Line line[maxn];
double dist(Point a,Point b)
{
return sqrt((a-b)*(a-b));
} bool cmp(Point a,Point b)
{
double t = (a-p0)^(b-p0);
if(sgn(t) > 0)return true;
else if(sgn(t) == 0 && sgn(dist(a,lis[0])-dist(b,lis[0])) <= 0)
return true;
else
return false;
} int main()
{
//freopen("in.txt","r",stdin);
int n,T;
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i = 0; i < n; i++)
{
scanf("%lf%lf",&lis[i].x,&lis[i].y);
}
int ans;
if(CalArea(lis,n) < 0)
reverse(lis,lis+n);
for(int i = 0; i < n; i++)
{
line[i] = Line(lis[i],lis[(i+1)%n]);
}
printf("%.2f\n",HPI(line,n,lis,ans));
}
return 0;
}
poj 1279 半平面交核面积的更多相关文章
- poj 1755 半平面交+不等式
Triathlon Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 6461 Accepted: 1643 Descrip ...
- poj 3335 /poj 3130/ poj 1474 半平面交 判断核是否存在 / poj1279 半平面交 求核的面积
/*************** poj 3335 点序顺时针 ***************/ #include <iostream> #include <cmath> #i ...
- poj 3525 半平面交求多边形内切圆最大半径【半平面交】+【二分】
<题目链接> 题目大意:给出一个四面环海的凸多边形岛屿,求出这个岛屿中的点到海的最远距离. 解题分析: 仔细思考就会发现,其实题目其实就是让我们求该凸多边形内内切圆的最大半径是多少.但是, ...
- POJ 3525 /// 半平面交 模板
题目大意: 给定n,接下来n行逆时针给定小岛的n个顶点 输出岛内离海最远的点与海的距离 半平面交模板题 将整个小岛视为由许多半平面围成 那么以相同的比例缩小这些半平面 一直到缩小到一个点时 那个点就是 ...
- POJ 3525 半平面交+二分
二分所能形成圆的最大距离,然后将每一条边都向内推进这个距离,最后所有边组合在一起判断时候存在内部点 #include <cstdio> #include <cstring> # ...
- POJ 3335 Rotating Scoreboard 半平面交求核
LINK 题意:给出一个多边形,求是否存在核. 思路:比较裸的题,要注意的是求系数和交点时的x和y坐标不要搞混...判断核的顶点数是否大于1就行了 /** @Date : 2017-07-20 19: ...
- poj 1271 && uva 10117 Nice Milk (半平面交)
uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem= ...
- poj 2451 Uyuw's Concert (半平面交)
2451 -- Uyuw's Concert 继续半平面交,这还是简单的半平面交求面积,不过输入用cin超时了一次. 代码如下: #include <cstdio> #include &l ...
- bzoj 2618 半平面交模板+学习笔记
题目大意 给你n个凸多边形,求多边形的交的面积 分析 题意\(=\)给你一堆边,让你求半平面交的面积 做法 半平面交模板 1.定义半平面为向量的左侧 2.将所有向量的起点放到一个中心,以中心参照进行逆 ...
随机推荐
- Django 个性化管理员站点
from django.contrib import admin # Register your models here. from .models import Moment class Momen ...
- GPUImage滤镜效果翻译
#import"GPUImageBrightnessFilter.h"//亮度 #import"GPUImageExposureFilter.h"//曝光 #i ...
- DenseNet
特点: dense shortcut connections 结构: DenseNet 是一种具有密集连接的卷积神经网络.在该网络中,任何两层之间都有直接的连接,也就是说,网络每一层的输入都是前面所有 ...
- PHP常见排序算法
$a = [1, 3, 5, 2, 4, 6, 12, 60, 45, 10, 32];$len = count($a);$num=0;/* * 冒泡排序 * 原理:不停的对相邻两个数进行比较,直到最 ...
- css3兼容IE8的方案 各个ie的hack
虽然现在很多项目已经对低版本IE不要求了,但是还有部分公司对IE8还是很执着的,咱作为屌丝前端程序员不能和老板说前端潮流,不能说趋势,只能动脑子了,下面就分享一些css3兼容ie8的方案思路.主要是实 ...
- Python-面向对象(二)-Day7
1.字段 12.方法 43.属性 63.1.属性的基本使用 73.2.实例:对于主机列表 83.3.属性的两种定义方式 94.对于类的成员而言都有两种形式: 144.1.私有成员和公有成员的访问限制不 ...
- Spring AOP AspectJ
本文讲述使用AspectJ框架实现Spring AOP. 再重复一下Spring AOP中的三个概念, Advice:向程序内部注入的代码. Pointcut:注入Advice的位置,切入点,一般为某 ...
- 记一次将公司网站http换成https
看了博客园将近一年了,一直都只是在被动的看,总觉得应该写点什么,但是又不知道该写点什么.今天正好公司要把网站由http换成https,那我就顺便记录一下吧. 由于之前没有弄过,所以就面向百度编程. 首 ...
- Python学习之list有序集合
# coding=utf-8 # list有序集合 classmate = ['Michael', 'Bob', 'Tracy'] print classmate print len(classmat ...
- 使用TortoiseSVN打Tag
参考了 https://blog.csdn.net/liuzx32/article/details/9123401. 值得注意的点是: 选择路径的时候,不要先点进去自己建好叶子节点路径再选择该路径,会 ...
