●BZOJ 2434: [Noi2011]阿狸的打字机

●赘述题目

（题意就不赘述了）

●解法：

●我先想的一个比较暴力的方法（要TLE）：

（ac自动机）先求出last数组（参见刘汝佳的解释：last[j]：表示j节点沿着失配指针往回走时，遇到的下一个单词节点（即单词在此结束）的编号），然后对输入的编号为y的字符串的每一个位置进行递归寻找是否能连上x字符串的结束节点。（给出失败代码片段图，就不解释了）

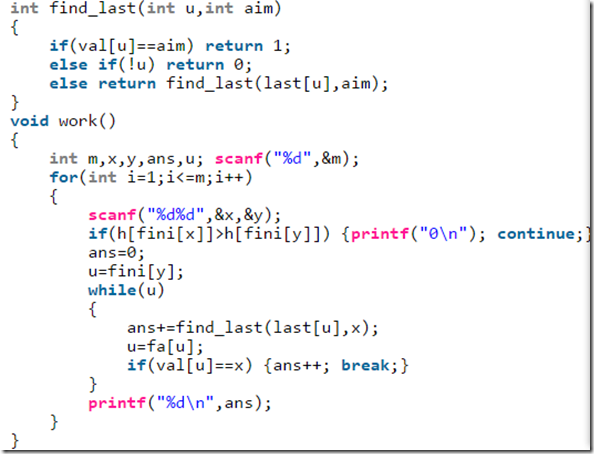
●正解：

（ac自动机）求出fail数组，然后以fail数组建树，如图

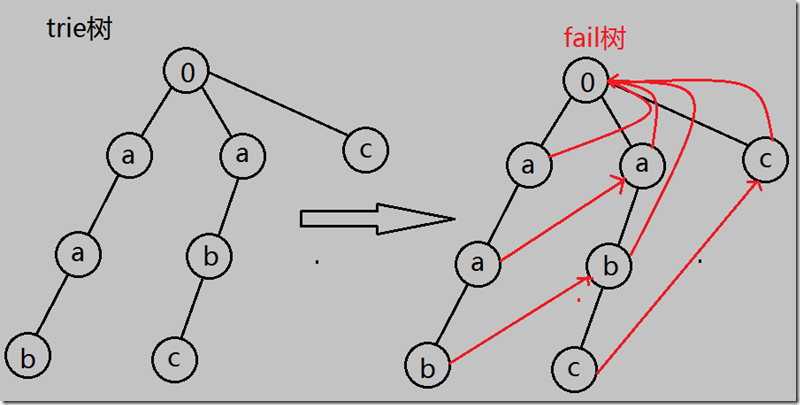
（看啊，红色的边和各点形成了另一棵树）

那么（看红树），若一个点在某个字符串结束节点的子树内，那么该字符串则出现在那个点所在的字符串里；如图中的a-b-c字符串和c字符串。

现在，我们若要求x字符串在y内出现了几次，就只需求以x的结束节点为根的子树内，有多少个节点是y字符串上的。

如何做呢？

将询问离线，y相同询问的弄在一起；

然后求出红树的dfs序（有点诡异，看代码）；

我们再遍历一遍输入的字符串：

对于输入的‘a’-‘z’，把对应的dfs序中其出现的位置的值加1，用树状数组维护；

对于输入的‘B’，现在的字符所对应的dfs序中的位置的值减1；

对于遇到的c个‘P’，我们不难发现，现在的树状树状维护的便是第c个字符串的每一个字符在dfs序中的位置的值所加1后的结果。接着便可用区间查询求出y==c的询问的答案。

那么上代码：

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<iostream>
using namespace std;
struct node{
	int x,y;
} q[100005];
struct edge{
	int to,next;
}e[200005];
int ch[100005][27];
int val[100005],fail[100005],fa[100005],fini[100005],l[100005],r[100005],ans[100005];
int head[100005],headq[100005],nxt[100005],lat[100005],c[150000];
char x[100005];
int cnt,pnt,ent=1,dnt,lx;
int idx(char x) {return x-'a';}
void modify(int u,int d) {for(int i=u;i<=dnt;i+=i&(-i)) c[i]+=d;}
int query(int u) {int sum=0;for(int i=u;i;i-=i&(-i)) sum+=c[i]; return sum;}
void add(int u,int v)
{
	e[ent]=(edge){v,head[u]};head[u]=ent++;
	e[ent]=(edge){u,head[v]};head[v]=ent++;
}
void read_trie()
{
	int u=0;
	for(int i=1;i<=lx;i++)
	{
		if(x[i]=='B') u=fa[u];
		else if(x[i]=='P') val[u]=++pnt,fini[pnt]=u;
		else
		{
			int c=idx(x[i]);
			if(!ch[u][c]) ch[u][c]=++cnt,fa[ch[u][c]]=u;
			u=ch[u][c];
		}
	}
}
void get_fail()
{
	queue<int> q;
	for(int c=0;c<26;c++) {int u=ch[0][c]; if(u) q.push(u);}
	while(!q.empty())
	{
		int r=q.front(); q.pop();
		for(int c=0;c<26;c++)
		{
			if(!ch[r][c]) continue;
			int u=ch[r][c];
			q.push(u);
			int v=fail[r];
			while(v&&!ch[v][c]) v=fail[v];
			fail[u]=ch[v][c];
		}
	}
}
//----------------------------------------------------------------------
void dfs_xu(int u,int fa)
{
	l[u]=++dnt;
	for(int i=head[u];i;i=e[i].next) if(e[i].to!=fa) dfs_xu(e[i].to,u);
	r[u]=dnt;
}
void work()
{
	int m; scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		scanf("%d%d",&q[i].x,&q[i].y);
		nxt[i]=lat[q[i].y];
		lat[q[i].y]=i;
	}
	for(int i=1;i<=cnt;i++) add(i,fail[i]);
	dfs_xu(0,0);
	int p=0,id=0;
	for(int i=1;i<=lx;i++)
	{
        if (x[i]=='P')
		{
            id++;
            for (int j=lat[id];j;j=nxt[j])
			{
                int u=fini[q[j].x];
                ans[j]=query(r[u])-query(l[u]-1);
            }
        }
        else if (x[i]=='B') modify(l[p],-1),p=fa[p];
        else p=ch[p][idx(x[i])],modify(l[p],1);
	}
	for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
}
int main()
{
	scanf("%s",x+1);
	lx=strlen(x+1);
	read_trie();
	get_fail();
	work();
	return 0;
}