[Codeforces]906D Power Tower
虽说是一道裸题,但还是让小C学到了一点姿势的。
Description
给定一个长度为n的数组w,模数m和询问次数q,每次询问给定l,r,求:
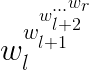
对m取模的值。
Input
第一行两个整数n,m,表示数组长度和模数。
接下来一行n个数,表示w数组。
接下来一行一个整数q,表示询问次数。
接下来q行,每行两个整数l,r,表示一次询问。
Output
对于每次询问,输出一行一个整数表示答案。
Sample Input
6 1000000000
1 2 2 3 3 3
8
1 1
1 6
2 2
2 3
2 4
4 4
4 5
4 6
Sample Output
1
1
2
4
256
3
27
597484987
HINT
1 ≤ n ≤ 105,1 ≤ m ≤ 109,1 ≤ wi ≤ 109,1 ≤ q ≤ 105,1 ≤ l ≤ r ≤ n。
Solution
看到这么清奇的式子,你大概会第一时间想到降幂大法吧?
先说说扩展欧拉定理,对于任意正整数a,b,p:
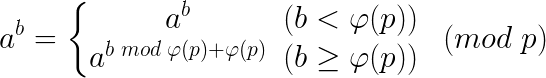
所以假设堆叠的幂次足够大,那么式子就可以转化为:


已知p经过至多2log次phi就会变成1。
所以递归求解,至多走到2log层模数就会变成1,所以返回0就行。
所以这道题就非常显然了,首先预处理出m的所有phi,对于每个询问,从l开始直接递归暴力,直到模数为1时返回。
还有一个问题,在求a^b%p的时候,怎么比较b和phi(p)的大小呢?
一种思路就是暴力计算a的后log项的值,注意还要特判1的情况,但这样写起来确实麻烦。
当然,有一种非常精妙的取模写法:
int modulo(ll x,int mod) {return x<mod?x:x%mod+mod;}
这是在做什么呢?这就是在比较b和phi(p)的大小,如果b<phi(p),返回b;否则返回b%phi(p)+phi(p)。
然后原式就变成了这样:

这样做看上去漏洞百出,可能的情况是,原本我们要计算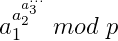 ,其中
,其中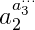 大等于
大等于 。
。
然而我们计算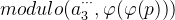 ,将
,将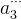 取模后,却发现
取模后,却发现 小于
小于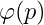 了。
了。
是否有这种可能呢?
其实就相当于判断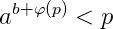 是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
是否有可能成立,我们可以发现,当a>2时式子是不可能成立的。
所以我们来看一看 是否有可能成立。
是否有可能成立。
有可能。
当且仅当p=6时,不等式成立。
然而6有什么特殊的性质呢?
我们发现phi(x)=6只有三个解:x=7,x=9或x=18。
所以接下来我们只要证明 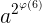 和
和 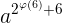 即
即 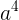 和
和 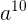 在对x取模的意义下相等即可。(其中phi(x)=6)
在对x取模的意义下相等即可。(其中phi(x)=6)
若a为x的倍数,显然它们对x取模都等于0,对于答案无影响。
当x=7时, ,所以
,所以 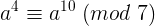 ;
;
当x=9时,若 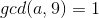 ,则影响同上;
,则影响同上;
若 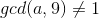 ,一定有
,一定有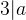 ,所以一定有
,所以一定有  ,
,
所以一定有 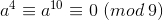 ,对于答案是没有影响的;
,对于答案是没有影响的;
当x=18时,若 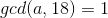 或
或 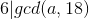 ,则影响同上;
,则影响同上;
我们有一个显然的结论:同余方程 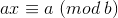 的解为
的解为 
若 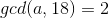 ,则
,则 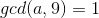 ,则
,则  ,则
,则 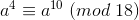
若 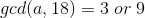 ,则
,则  且
且 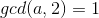 ,则
,则 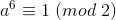 ,则
,则 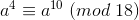
所以综上,我们就证明了该算法的正确性。
时间复杂度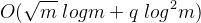 。
。
#include <cstdio>
#include <cstring>
#include <algorithm>
#define ll long long
#define MN 100005
using namespace std;
int a[MN],mod[MN];
int n,p;
bool fg; inline int read()
{
int n=,f=; char c=getchar();
while (c<'' || c>'') {if(c=='-')f=-; c=getchar();}
while (c>='' && c<='') {n=n*+c-''; c=getchar();}
return n*f;
} inline int pro(ll x,int md) {return x<md?x:x%md+md;}
inline int mi(int x,int y,int md)
{
register int z=;
for (;y;x=pro(1LL*x*x,md),y>>=)
if (y&) z=pro(1LL*z*x,md);
return z;
} int dfs(int x,int y,int lim)
{
if (x==lim) return a[x]>=mod[y]?a[x]%mod[y]+mod[y]:a[x];
if (mod[y]==) return ;
return mi(a[x],dfs(x+,y+,lim),mod[y]);
} int main()
{
register int i,j,x,y;
n=read(); mod[]=read();
for (i=;mod[i]>;++i)
{
mod[i+]=x=mod[i];
for (j=;j*j<=x;++j)
{
for (fg=;x%j==;x/=j,fg=true);
if (fg) mod[i+]=1LL*mod[i+]*(j-)/j;
}
if (x>) mod[i+]=1LL*mod[i+]*(x-)/x;
}
for (i=;i<=n;++i) a[i]=read();
for (p=read();p;--p)
{
x=read(); y=read();
printf("%d\n",dfs(x,,y)%mod[]);
}
}
Last Word
打Codeforces的时候正纳闷这种情况该怎么处理,却发现大佬们清一色都是这么写的。
小C觉得自己的证明蠢得不行啊……
如果读者有更直观的证明该算法的正确性的方法请务必告诉小C。
[Codeforces]906D Power Tower的更多相关文章
- CodeForces - 906D Power Tower(欧拉降幂定理)
Power Tower CodeForces - 906D 题目大意:有N个数字,然后给你q个区间,要你求每一个区间中所有的数字从左到右依次垒起来的次方的幂对m取模之后的数字是多少. 用到一个新知识, ...
- Codeforces 906D Power Tower(欧拉函数 + 欧拉公式)
题目链接 Power Tower 题意 给定一个序列,每次给定$l, r$ 求$w_{l}^{w_{l+1}^{w_{l+2}^{...^{w_{r}}}}}$ 对m取模的值 根据这个公式 每次 ...
- Codeforces Round #454 (Div. 1) CodeForces 906D Power Tower (欧拉降幂)
题目链接:http://codeforces.com/contest/906/problem/D 题目大意:给定n个整数w[1],w[2],……,w[n],和一个数m,然后有q个询问,每个询问给出一个 ...
- [CodeForces - 906D] Power Tower——扩展欧拉定理
题意 给你 $n$ 个 $w_i$ 和一个数 $p$,$q$个询问,每次询问一个区间 $[l,r] $,求 $w_l ^{w_{l+1}^{{\vdots}^{w_r}}} \ \% p$ 分析 由扩 ...
- CodeForces 907F Power Tower(扩展欧拉定理)
Priests of the Quetzalcoatl cult want to build a tower to represent a power of their god. Tower is u ...
- 【CodeForces】906 D. Power Tower 扩展欧拉定理
[题目]D. Power Tower [题意]给定长度为n的正整数序列和模数m,q次询问区间[l,r]累乘幂%m的答案.n,q<=10^5,m,ai<=10^9. [算法]扩展欧拉定理 [ ...
- Codeforces Round #454 D. Power Tower (广义欧拉降幂)
D. Power Tower time limit per test 4.5 seconds memory limit per test 256 megabytes input standard in ...
- CodeForces 906D (欧拉降幂)
Power Tower •题意 求$w_{l}^{w_{l+1}^{w_{l+2}^{w_{l+3}^{w_{l+4}^{w_{l+5}^{...^{w_{r}}}}}}}}$ 对m取模的值 •思路 ...
- [CodeForces - 1225D]Power Products 【数论】 【分解质因数】
[CodeForces - 1225D]Power Products [数论] [分解质因数] 标签:题解 codeforces题解 数论 题目描述 Time limit 2000 ms Memory ...
随机推荐
- djangoueditor 集成xadmin
1.安装Python3兼容版本 https://github.com/twz915/DjangoUeditor3/ 2.model加入字段 from DjangoUeditor.models impo ...
- 亚马逊的PuTTY连接AWS出现network error connection refused,终极解决方案。
使用PuTTY连接AWS的时候,一直出现network error connection refused.百度了这个问题,大家都说是SSH要设置成22.但是我已经设置过了,为什么还是遇到这个问题呢? ...
- Hibernate之SQL查询
Hibernate支持使用原生的SQL语句进行查询.使用原生的SQL的好处是:可以利用某些数据库的特性(不同的数据库SQL 语法会有所差异), 将原有的使用JDBC作为持久层技术的应用 ,迁移到使用H ...
- Angular组件——组件生命周期(一)
组件声明周期以及angular的变化发现机制 红色方法只执行一次. 变更检测执行的绿色方法和和组件初始化阶段执行的绿色方法是一个方法. 总共9个方法. 每个钩子都是@angular/core库里定义的 ...
- Vim 游戏 2048
给大家介绍一款可以在Vim里面玩的游戏 vim2048. 界面如图: 操作非常简单,可以用 hjkl 或者 上下左右方向键移动 项目开源地址为: https://github.com/wsdjeg/v ...
- Spring+Hibernate+Struts(SSH)框架整合
SSH框架整合 前言:有人说,现在还是流行主流框架,SSM都出来很久了,更不要说SSH.我不以为然.现在许多公司所用的老项目还是ssh,如果改成流行框架,需要成本.比如金融IT这一块,数据库dao层还 ...
- OAuth是什么?
一.OAuth的概念 1.问题的提出 2.应用场景 3.规范演进 二.OAuth的运行原理 1.参与者 访问私有数据需要用户参与(客户.用户.服务提供者) 访问公共数据不需要用户参与(客户.服务提供者 ...
- Excel 日期截取(函数)
需求:时间段截取,去掉年月日,保留时分. 实现函数: =TEXT(A2,"HH:MM")&"-"&TEXT(B2,"HH:MM& ...
- nginx配置反向代理详细教程(windows版)
内容属于原创,如果需要转载,还请注明地址:http://www.cnblogs.com/j-star/p/8785334.html Nginx是一款轻量级的Web 服务器/反向代理服务器及电子邮件(I ...
- win7远程桌面 连接不上(用户名与全名不匹配的问题)
用户名与用户全名不一致导致的.我刚也是这个问题,折腾够了好久.你先看看 计算机右键→管理→本地用户和组→用户 找到你需要远程的管理员账户,看看名称与全名是否一致,若不一致,继续看下面.1.按" ...
