逆卷积的详细解释ConvTranspose2d（fractionally-strided convolutions)

1.首先先定义进行卷积的参数：

• 输入特征图为高宽一样的H_in*H_in大小的x
• 卷积核大小kernel_size
• 步长stride
• padding填充数(填充0)
• 输出特征图为H_out*H_out大小的y

计算式子为：

H_out =  floor( H_in + 2*padding - kernel_size / stride) + 1

2.然后实现上面的卷积的转置卷积

定义其参数为：

• 输入特征图为高宽一样的H_out*H_out大小的y
• 卷积核大小kernel_size
• 步长stride
• padding_new 填充数(填充0)
• 输出特征图为H_in*H_in大小的x

逆卷积的过程主要分两步：

• 对输入的特征图y进行变换，得到新的特征图y_new

1. 内部变换，与卷积时设置的stride相关
2. 外部变换，与卷积时设置的padding相关

• 根据得到的特征图进行卷积即可

1）对输入的特征图y进行变换，得到新的特征图y_new

1》内部变换

当卷积时设置的stride>1时，将对输入的特征图y进行插值操作(interpolation)。

即需要在输入的特征图y的每个相邻值之间插入(stride-1)行和列0，因为特征图中能够插入的相邻位置有(height-1)个位置，所以此时得到的特征图的大小由H_out*H_out(H_out即height) 变为新的 H_{out_new}*H_{out_new}，即[H_out + (stride-1) * (H_out-1)] * [H_out + (stride-1) * (H_out-1)]

2》外部变换

为了实现由H_out*H_out大小的y逆卷积得到H_in*H_in大小的x，还需要设置padding_new的值为(kernel_size - padding - 1),这里的padding是卷积操作时设置的padding值

所以计算式子变为：

H_in =  floor( [H_{out_new} + 2*padding_new - kernel_size] / stride') + 1

⚠️该式子变换后，定义向下取整的分母stride'值为定值1

H_{out_new}和padding_new的值代入上面的式子，即变为：

H_in =  floor( H_out + (stride-1) * (H_out-1) + 2*(kernel_size - padding - 1) - kernel_size) + 1

化简为：

H_in =  floor( (H_out - 1) * stride - 2*padding + kernel_size - 1) + 1

= (H_out - 1) * stride - 2*padding + kernel_size

这样式子使的卷积Conv2d和逆卷积ConvTranspose2d在初始化时具有相同的参数，而在输入和输出形状方面互为倒数。

所以这个式子其实就是官网给出的式子：

可见这里没考虑output_padding

output_padding的作用：可见nn.ConvTranspose2d的参数output_padding的作用

3.下面举例说明

https://github.com/vdumoulin/conv_arithmetic#convolution-arithmetic

1）当stride=1时，就不会进行插值操作，只会进行padding，举例说明：

卷积操作为：

蓝色为输入特征图H_in*H_in=4*4，绿色为输出特征图H_out*H_out=2*2，卷积核kernel_size=3, stride=1

根据式子H_out =  floor( H_in + 2*padding - kernel_size / stride) + 1

可得padding=0

其对应的逆卷积操作为：

蓝色为输入特征图H_out*H_out=2*2，绿色为输出特征图H_in*H_in=4*4，卷积核kernel_size=3, stride=1

卷积时的padding=0

将这些值代入上面的式子H_in = (H_out - 1) * stride - 2*padding + kernel_size

果然输入H_out*H_out=2*2能得到输出H_in*H_in=4*4

变形过程为：

padding_new = kernel_size - padding -1 = 3 -0 -1 = 2

所以可见下方的蓝色最后的大小为7*7 = H_out + 2*padding_new = 2 + 2*2 = 6

⚠️这里可见是有padding的，为什么定义是为no padding呢？

这是因为它对应的卷积操作的padding=0

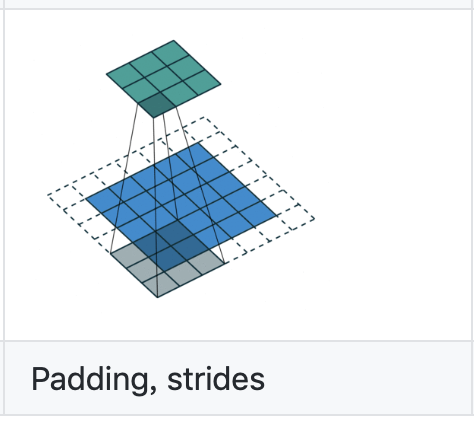
1）当stride=2时，进行插值和padding操作，举例说明：

卷积操作为：

蓝色为输入特征图H_in*H_in=5*5，绿色为输出特征图H_out*H_out=3*3，卷积核kernel_size=3, stride=2

根据式子H_out =  floor( H_in + 2*padding - kernel_size / stride) + 1

可得padding=1

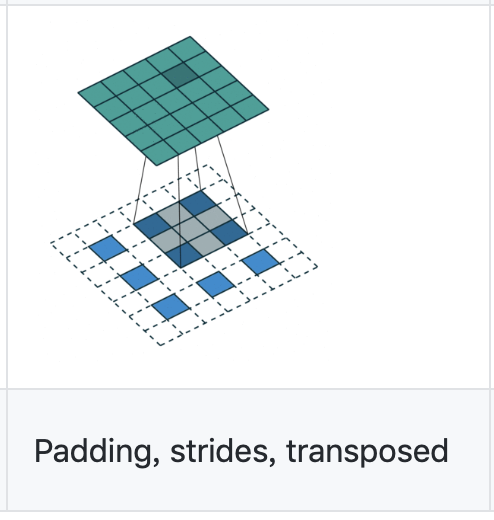
其对应的逆卷积操作为：

蓝色为输入特征图H_out*H_out=3*3，绿色为输出特征图H_in*H_in=5*5，卷积核kernel_size=3,stride=2

卷积时的padding=1

将这些值代入上面的式子H_in = (H_out - 1) * stride - 2*padding + kernel_size

果然输入H_out*H_out=3*3能得到输出H_in*H_in=5*5

变形操作为：

H_{out_new} = H_out + (stride-1) * (H_out-1) = 3 + (2-1)*(3-1) = 5

padding_new = kernel_size - padding -1 = 3 -1 -1 = 1

所以可见下方的蓝色最后的大小为7*7 = H_{out_new} + 2*padding_new = 5 + 2*1 = 7

⚠️因为这里的逆卷积对应的卷积操作的padding= 1，所以这里不是no padding,而是padding