关于ASL(平均查找长度)的简单总结

ASL（Average Search Length），即平均查找长度，在查找运算中，由于所费时间在关键字的比较上，所以把平均需要和待查找值比较的关键字次数成为平均查找长度。

它的定义是这样的：

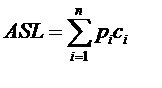
其中n为查找表中元素个数，Pi为查找第i个元素的概率，通常假设每个元素查找概率相同，Pi=1/n，Ci是找到第i个元素的比较次数。

当然，有查找成功，就有查找不成功，即要查找元素不在查找表中。针对不同查找方式的查找成功与不成功，我接下来会说，这也是一我一开始有点乱的地方。

一个算法的ASL越大，说明时间性能差，反之，时间性能好，这也是显而易见的。

• 在顺序查找(Sequence Search)表中，查找方式为从头扫到尾，找到待查找元素即查找成功，若到尾部没有找到，说明查找失败。所以说，Ci（第i个元素的比较次数）在于这个元素在查找表中的位置，如第0号元素就需要比较一次，第一号元素比较2次......第n号元素要比较n+1次。所以Ci=i；所以

　　　　

可以看出，顺序查找方法查找成功的平均 比较次数约为表长的一半。当待查找元素不在查找表中时，也就是扫描整个表都没有找到，即比较了n次，查找失败

• 折半查找(Binary Search)，首先待查找表是有序表，这是折半查找的要求。在折半查找中，用二叉树描述查找过程，查找区间中间位置作为根，左子表为左子树，右子表为右子树，，因为这颗树也被成为判定树(decision tree)或比较树(Comparison tree)。查找方式为(找k)，先与树根结点进行比较，若k小于根，则转向左子树继续比较，若k大于根，则转向右子树，递归进行上述过程，直到查找成功或查找失败。在n个元素的折半查找判定树中，由于关键字序列是用树构建的，所以查找路径实际为树中从根节点到被查结点的一条路径，因为比较次数刚好为该元素在树中的层数。所以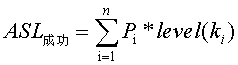Pi为查找k的概率，level(Ki)为k对应内部结点的层次。而在这样的判定树中，会有n+!种查找失败的情况，因为将判定树构建为完全二叉树，又有n+1个外部结点(用Ei(0<=i<=n)表示)，查找失败，即为从根结点到某个外部结点也没有找到，比较次数为该内部结点的结点数个数之和，所以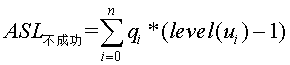，qi表示查找属于Ei中关键字的概率，level(Ui)表示Ei对应外部结点的层次。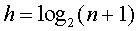所以，在一颗有n个结点判定树中，总数，所以判定树高度为的满二叉树,第i层上结点个数为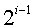，查找该层上的结点需要进行i次比较，因此，在等概率情况下ASL为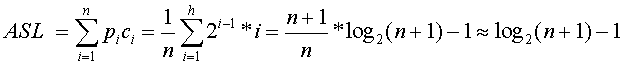
• 例：给11个数据元素有序表（2,3,10,15,20,25,28,29,30,35,40）采用折半查找。则ASL成功和不成功分别是多少？首先画出判定树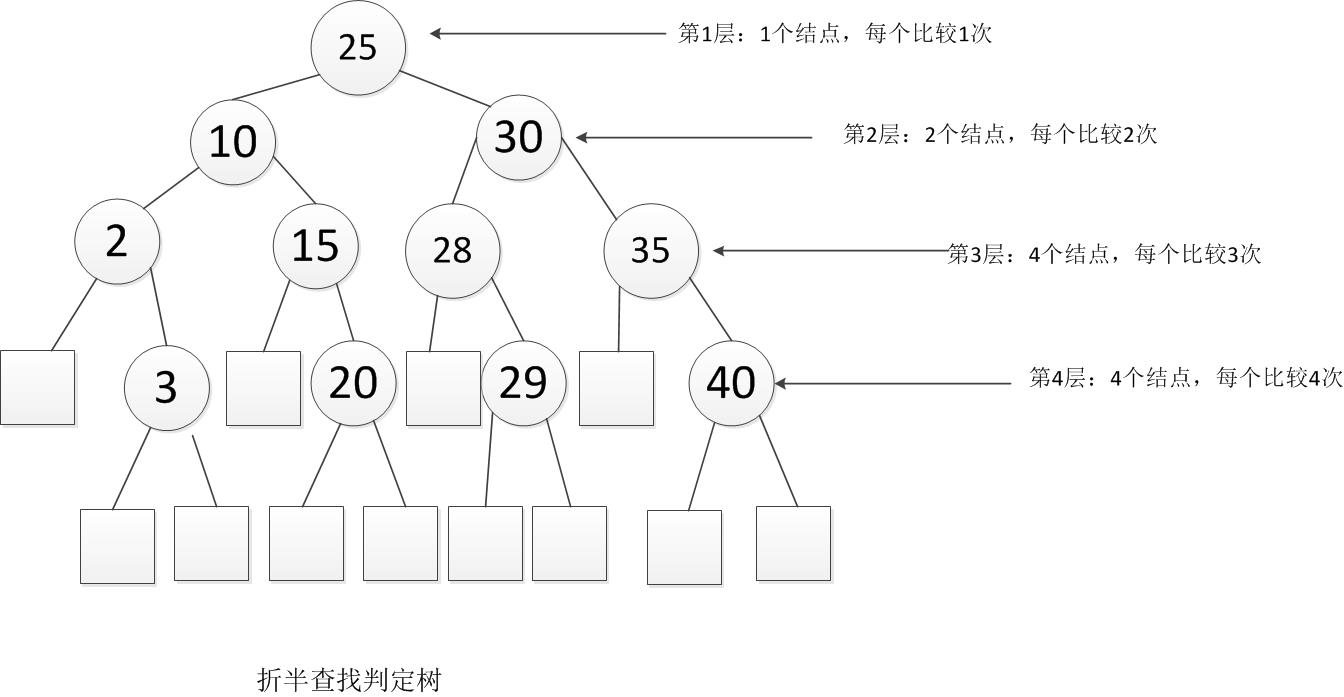，     查找成功时总会找到途中某个内部结点，所以成功时的平均查找长度为 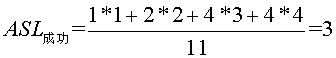即25查找一次，成功，10,30要查找2次，成功，2,15,28,35要查找3次，成功，3,20,29,40要查找4次，成功。 而不成功的平均查找长度为  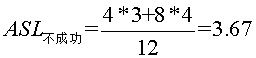，为什么这么算呢，因为内部结点都能查找成功，而查找不成功的就是那些空的外部结点，所以到查询到2的左孩子，15的左孩子，28的左孩子，35的左孩子，3的左右孩子，20的左右孩子，29的左右孩子，40的左右孩子时，都是查找不成功的时候。如我要找1，比25小，转向左子树，比较一次，比10小，转左子树，2次，比2 小，转左子树，3次，此时2无左子树，所以失败。所以 。

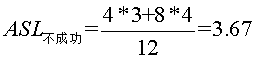• 哈希表中的ASL   查找成功的平均查找长度是指查找到哈希表中已有关键字的平均探测次数。而查找不成功的平均查找长度是指在哈希表中找不到待查的元素，最后找到空位置元素的探测次数平均值。

• 例：散列表长度为13，地址空间为0~12，散列函数H(k) =K mod 13,对关键字序列{19,14,23,01,68,20,84,27,55,11,10,79}  所以线性探测结果为：

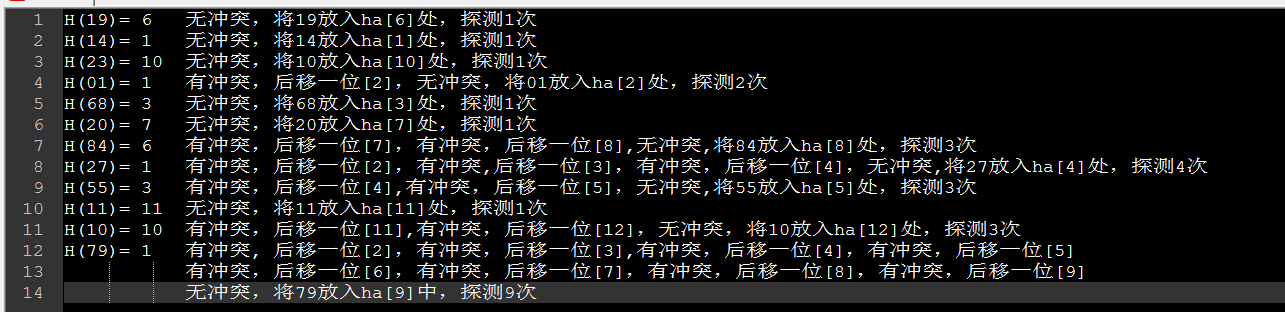
根据探测次数，

　　　　

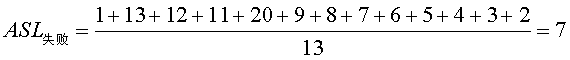 当然成功的很好理解，12个元素，每个元素的探测次数之和除以12就行。而不成功的计算是这样的。散列表长度为13，根据定义，假设待查关键字不在散列表中，要一直找到空元素才算查找失败，如H[0]为空，与待查找元素不等，不成功，比较一次，H[1]，此时H[1]的元素与原本放在H[1]的元素不等(假设不在散列表在之中，但也不是空的)，继续向后比，与H[2]比也不等，继续向后，一直到H[12]，也不等，继续向后时，回到H[0]，为空，也不等，查找失败，总计比较13次，然后计算第二号元素，一样的比较，一直把每个位置都统计一遍，从而得出ASL不成功的.

• 以上就是对ASL的小小总结，为了加强自己的理解，也便于自己以后的回顾和修改，还有有一点很开心的是，最为新兰党，总算让我在2019年初等到了洗衣机和兰酱的休学旅行，很满意了。