oo第二阶段总结

第五次作业——多线程电梯

一、设计策略

　　本次作业是我们第一次接触多线程，给程序添加多线程功能后最大的挑战是实现共享数据的安全、避免冲突，由于这次作业是第一次尝试多线程方法，因此采用了将所有方法都加上synchronized修饰符的方法来避免数据冲突。

二、程序结构

　

　　由于本次作业完成的比较匆忙，因此并没有全面的实现多线程的方式，且在测试中出现了较多的bug。由类图可以看出，程序分类较为简单，每个类的功能太过集中，有违oo的设计原则，同时，方法的数目也相对较少，随之而来的是较多的重复代码，这是极为不好的代码风格，同时也违背了oo编程原则。

三、程序的bug

　　本次作业程序的bug主要集中在线程安全控制，程序在运行过程中会随机出现不可控的输出结果，这与刚开始的多线程设计不明确有很大的关系。同时，这次作业并没有采取wait-notifyall模式，这也是使得程序出现bug的一大因素。

四、心得体会

　　多线程较为复杂，且带有随机性，因此会提高debug的难度，这就要求我们在开始设计时就规划好程序运行的方案流程，避免中途或者最后再进行大规模修改，这样反而容易产生更多的bug。

第六次作业——IFTTT

一、设计策略

　　IFTTT主要由监听器和任务组成，因此，程序设计为：为每个监听任务开创一个线程进行监听，每当监听到规定动作后，调用相应方法进行任务响应，线程之间只是调用的方法相同，并不存在数据上的冲突。

二、程序结构

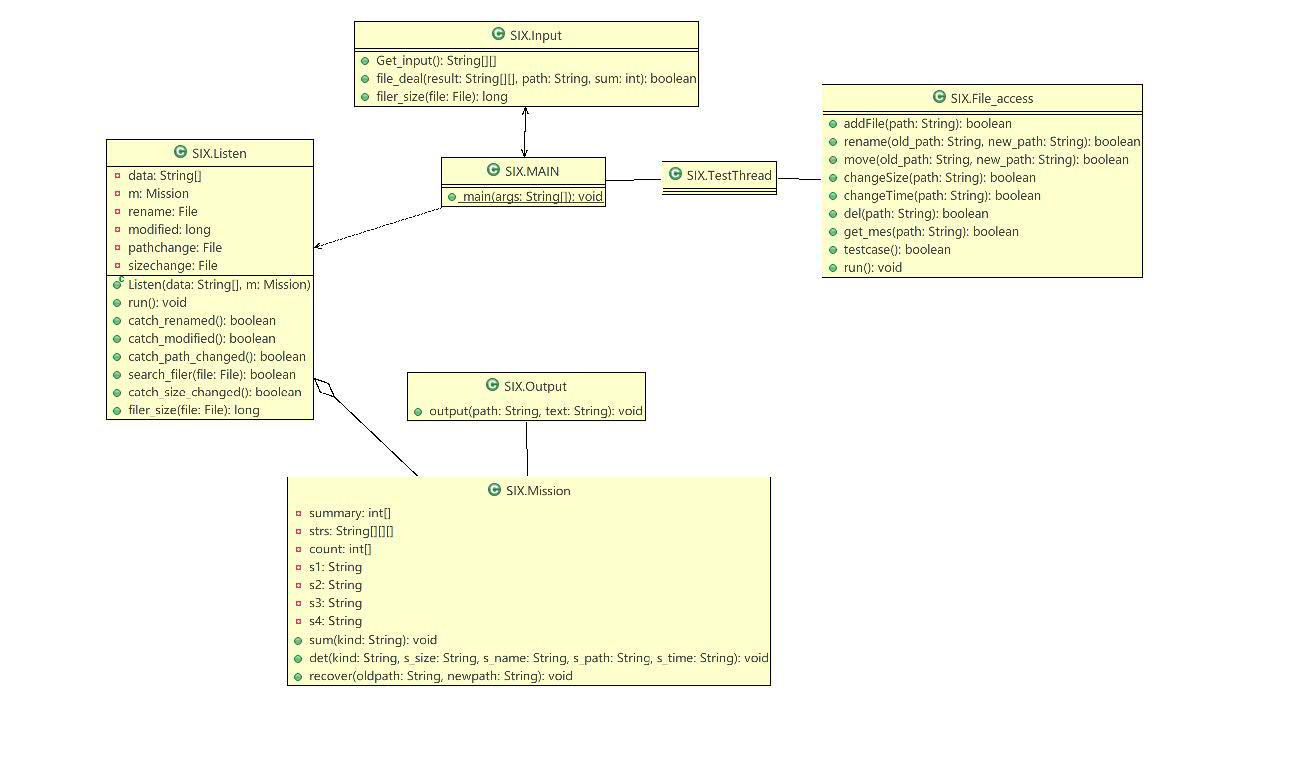
　　本次作业已能较为熟练地掌握多线程的使用，并且进行系统性的设计与测试。程序通过Input类读入监听器以及相应的任务，之后创立相应的线程，监听事件的发生，当事件发生后，做出相应的响应。测试者可通过testthread来制造相应的事件来测试程序的相应。

三、程序的bug

　　由于我的测试者并没有测试我的程序，这里只简述我自己尚未解决的bug。这些bug主要是细节方面的问题，比如多层文件夹的监控以及同层文件的监控选择问题，bug出现的原因主要是在方法设计时时间较为紧迫，因此只实现了获取监控文件信息的基本功能，并没有对其进行完整的拓展。

四、新的体会

　　对于成体系的复杂的程序设计，要多尝试，不能因为复杂而望而却步，停滞不前，事实证明，只要着手去做，总会找到解决方案。

第七次作业——出租车

一、设计策略

　　此次作业的出租车调动系统由100量出租车和80*80的地图网以及