基本思想

模型已定，参数未知

根据已存在的样本，挑选（求出）能让样本以最大概率发生的参数

极大似然估计和最小二乘法最大区别之一 极大似然需要知道概率密度函数（离散型叫分布律）

若总体X属离散型，其分布律的形式是已知，为待估参数，是的取值范围

是来自的样本，的样本值为，则的联合分布律为：

似然函数就是样本都发生的概率，即联合概率，公式如下

求解思路

（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数，令导数为0，得到似然方程；

（4）解似然方程，得到的参数即为所求；

示例

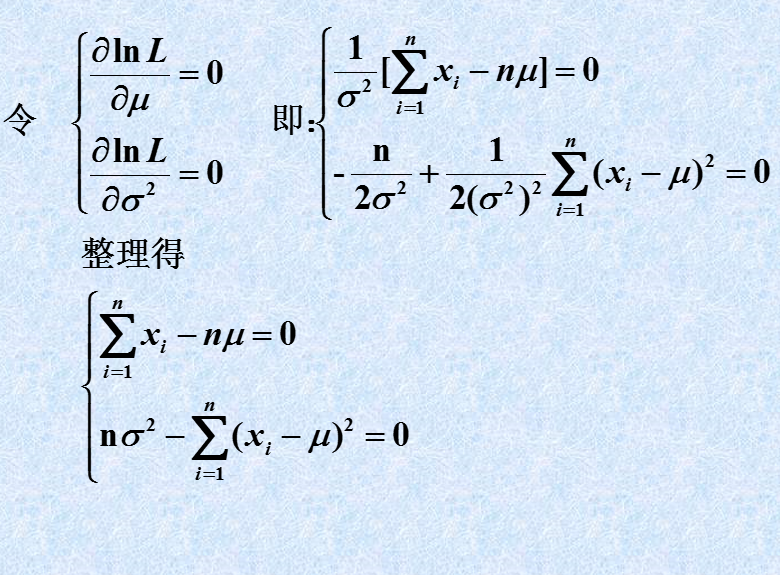
引用自http://blog.csdn.net/weiyudang11/article/details/51523836

极大似然估计（MLE)的更多相关文章

  1. 理解极大似然估计(MLE)

    极大似然估计学习时总会觉得有点不可思议,为什么可以这么做,什么情况才可以用极大似然估计.本文旨在通俗理解MLE(Maximum Likelihood Estimate). 一.极大似然估计的思想与举例 ...

  2. 机器学习（二十五）— 极大似然估计（MLE）、贝叶斯估计、最大后验概率估计（MAP）区别

    最大似然估计(Maximum likelihood estimation, 简称MLE)和最大后验概率估计(Maximum aposteriori estimation, 简称MAP)是很常用的两种参 ...

  3. 数理统计7：矩法估计（MM）、极大似然估计（MLE），定时截尾实验

    在上一篇文章的最后,我们指出,参数估计是不可能穷尽讨论的,要想对各种各样的参数作出估计,就需要一定的参数估计方法.今天我们将讨论常用的点估计方法:矩估计.极大似然估计,它们各有优劣,但都很重要.由于本 ...

  4. 浅议极大似然估计（MLE）背后的思想原理

    1. 概率思想与归纳思想 0x1:归纳推理思想 所谓归纳推理思想,即是由某类事物的部分对象具有某些特征,推出该类事物的全部对象都具有这些特征的推理.抽象地来说,由个别事实概括出一般结论的推理称为归纳推 ...

  5. MLE极大似然估计和EM最大期望算法

    机器学习十大算法之一:EM算法.能评得上十大之一,让人听起来觉得挺NB的.什么是NB啊,我们一般说某个人很NB,是因为他能解决一些别人解决不了的问题.神为什么是神,因为神能做很多人做不了的事.那么EM ...

  6. （转载）极大似然估计&最大后验概率估计

    前言 不知看过多少次极大似然估计与最大后验概率估计的区别,但还是傻傻分不清楚.或是当时道行太浅,或是当时积累不够. 这次重游机器学习之路,看到李航老师<统计学习方法>中第一章关于经验风险最 ...

  7. [白话解析] 深入浅出 极大似然估计 & 极大后验概率估计

    [白话解析] 深入浅出极大似然估计 & 极大后验概率估计 0x00 摘要 本文在少用数学公式的情况下,尽量仅依靠感性直觉的思考来讲解 极大似然估计 & 极大后验概率估计,并且从名著中找 ...

  8. 机器学习基础系列--先验概率 后验概率 似然函数 最大似然估计(MLE) 最大后验概率(MAE) 以及贝叶斯公式的理解

    目录 机器学习基础 1. 概率和统计 2. 先验概率(由历史求因) 3. 后验概率(知果求因) 4. 似然函数(由因求果) 5. 有趣的野史--贝叶斯和似然之争-最大似然概率(MLE)-最大后验概率( ...

  9. 极大似然估计、贝叶斯估计、EM算法

    参考文献:http://blog.csdn.net/zouxy09/article/details/8537620 极大似然估计 已知样本满足某种概率分布,但是其中具体的参数不清楚,极大似然估计估计就 ...

随机推荐

  1. 关于layer的坑

    真是自己给自己挖坑,坑死人不偿命啊. 在用layui开发时,遇到这种情况,点击按钮出现一个弹出层,然而我不是用button按钮去实现的,而是用a标签做的,本来a标签也是可以实现的,在这里我无形中给自己 ...

  2. webpack的安装与使用

    在安装 Webpack 前,你本地环境必须已安装nodejs. 可以使用npm安装,当然由于 npm 安装速度慢,也可以使用淘宝的镜像及其命令 cnpm,安装使用介绍参照:使用淘宝 NPM 镜像. 使 ...

  3. 两种方法上传本地文件到github

    https://www.jianshu.com/p/c70ca3a02087 自从使用github以来,一直都是在github网站在线上传文件到仓库中,但是有时因为网络或者电脑的原因上传失败.最重要的 ...

  4. SVN报Previous operation has not finished; run 'cleanup'&

    做着项目突然SVN报Previous operation has not finished; run 'cleanup' if it was interrupted,进度又要继续,烦.百度一下发现很多 ...

  5. Html Mailto标签详细使用方法

    http://www.360doc.com/content/09/0805/14/16915_4684377.shtml Html Mailto标签详细使用方法 Html中mailto标签是一个非常实 ...

  6. Python 3 利用 Dlib 19.7 和 sklearn机器学习模型 实现人脸微笑检测

    0.引言  利用机器学习的方法训练微笑检测模型,给一张人脸照片,判断是否微笑:   使用的数据集中69张没笑脸,65张有笑脸,训练结果识别精度在95%附近: 效果: 图1 示例效果 工程利用pytho ...

  7. 使用git bash提交代码到github托管

    1.首先登录到https://github.com注册Github帐号,并且创建一个repository.  或者登录到  https://git.oschina.net/注册账号,并且创建一个rep ...

  8. 关于Serializable的serialVersionUID

    在实现了Serializable接口的class中,需要声明一个long serialVersionUID,用来标明当前class的版本号,但很多人在编程时,总是不原意去声明这个serialVersi ...

  9. UWP: 实现 UWP 应用自启动

    在上一篇文章中,我们实现了使用命令行来启动 UWP 应用,在这一篇文章中,我们会实现 UWP 应用自启用的实现,也即开机后或用户登陆后,应用自己启动.这些特性原来都是 Win32 程序所具备的,UWP ...

  10. java面向对象——类

    一.类 类(class)是构造对象的模板或蓝图.由类构造(construct)对象的过程称为创建类的实例(instance). 用 java 编写的所有代码都位于某个类的内部.标准的Java 库提供了 ...