夏令营讲课内容整理 Day 6 Part 3.

第三部分主要讲的是倍增思想及其应用。

在Day3的整理中，我简要提到了倍增思想，我们来回顾一下。

倍增是根据已经得到的信息，将考虑的范围扩大一倍，从而加速操作的一种思想，它在变化规则相同的情况下，加速状态转移。

运用倍增方法预处理信息，可以加速询问。

如果题目的数据范围极大，线性时间也不够用，那就可以考虑倍增思想了。

 

1.快速幂

计算 a^x % p。

暴力是显然的，TLE。

其实就是想办法把x拆开。考虑先把它表示成二进制形式，我们可以用不超过logx个f[i]拼出我们想要的答案。

在x的二进制表示中，1表示“取”。二进制中的每一个1都表示2的i次方。

比如说计算a^100，100的二进制是01100100，可以看出在2^2，2^5，2^6位置是1，而这些数分别对应4,32,64，那么只需要把a^100拆分成a^64*a^32*a^4即可。

实现很容易，每次提取处最低的二进制位再除以2即可。

long long int fast_pow(long long int a,long long int x,long long int p){
    long long int ans = ;
    long long int sum = a % p;
    for (;x;x>>=,sum = sum*sum%p)
        if (x&)
            ans = ans*sum%p;
    return ans;
}

 

2.树上祖先

给定一棵N个节点的树，告诉你每个节点的父亲是谁，做Q次询问，每次询问某个点的k倍祖先是谁。

暴力做法显然，O(QN)。

有一种优化是预处理出每个点向后跳1~B步的点是哪个，每次询问B步B步地跳，当B = √N时，复杂度取得最优O（N√N）。

改进一下这个优化，预处理出每个点向父亲跳2^i步是谁，这样每次至多跳logN步就能跳到目标位置。

假设跳k步，考虑k的二进制表示，二进制中的每一个1都表示2^i，拼凑k。

每跳一步相当于删去一个1.

我们设f[i][j]为第i个元素向父亲跳2^j步是谁，则边界是f[i][0]为第i个元素的父亲。

转移：f[i][j] = f[f[i][j]-1][j-1]

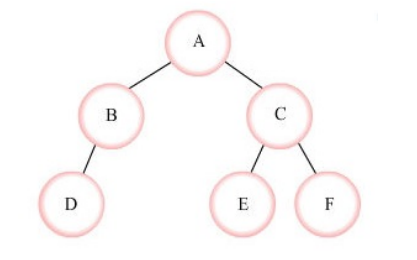
for (int i=;i<=N;i++)
　　for (int j=;i+(<<i)-<=N,i++)
　　　　f[i][j] = f[f[i][j]-][j-];

查询：

int q(int x,int k){
　　for (int i=N;i>=;i--)
　　　　if (k & ( << i))
　　　　　　x = f[x][i];
　　return x;
}

3.倍增LCA

参阅Day3整理

 

4.ST表

用来维护区间信息。对于重复信息只会贡献一次的信息，我们可以用ST表来实现高效查询。

还是倍增思想，预处理每个位置向后2^i长度的信息，假设我们要查询的是[L,R]，可以通过两段长度为2^k长度的区间覆盖[L,R]，k = floor(log(R-L+1))

以区间最小值举例，预处理时先枚举i再枚举j，f[i][j] = min(f[i-1][j],f[i-1][j+(1 << i-1)])

查询时,ans = min(f[k][l],f[k][r-(1 << k)+1])

ST表可以维护最大值，最小值，gcd等，但不能维护求和等信息，因为这样会重复计算。同时也不支持修改，所以是一个比较弱的数据结构。

不过，ST表可以完成树上LCA的查询。用它记录树的欧拉序，也就是说，在每次遍历到这个节点时都将其记录下来。

所谓欧拉序，就是记录你DFS一棵树的时候的遍历轨迹。

比如说这样一棵树：

 

它的欧拉序是ABDBACECFCA

可以知道，对于一个有N个节点的树，其欧拉序的长度为2N-1。

记x第一次出现的位置为fir[x]，有一个结论：

对于两个节点u,v，欧拉序[fir[u],fir[v]]这段区间中的深度最浅的那个节点，是lca(u,v)。

因为u,v之间的路径上的节点都会出现在这段区间。深度比u,v的lca的小的节点不会出现在这段区间。维护欧拉序中的每个位置，向后2^i的区间中深度最浅的节点是谁。

查询方式和刚才上边那个例子类似，用那个做法查询[fir[u],fir[v]]这一段的最小值就好。