Python 二分查找

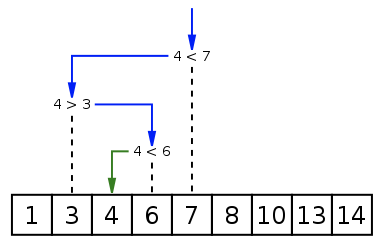
（非递归实现）

def binary_search(alist, item):
      first = 0
      last = len(alist)-1
      while first<=last:
          midpoint = (first + last)/2
          if alist[midpoint] == item:
              return True
          elif item < alist[midpoint]:
              last = midpoint-1
          else:
              first = midpoint+1
    return False
testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

（递归实现）

def binary_search(alist, item):
    if len(alist) == 0:
        return False
    else:
        midpoint = len(alist)//2
        if alist[midpoint]==item:
          return True
        else:
          if item<alist[midpoint]:
            return binary_search(alist[:midpoint],item)
          else:
            return binary_search(alist[midpoint+1:],item)

testlist = [0, 1, 2, 8, 13, 17, 19, 32, 42,]
print(binary_search(testlist, 3))
print(binary_search(testlist, 13))

• 最优时间复杂度：O(1)
• 最坏时间复杂度：O(logn)

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。