Mahout系列之----距离度量
x = (x1,...,xn) 和y = (y1,...,yn) 之间的距离为
(1)欧氏距离 EuclideanDistanceMeasure

(2)曼哈顿距离 ManhattanDistanceMeasure
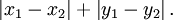
(3)马氏距离MahalanobisDistanceMeasure
马氏距离是由印度统计学家马哈拉诺比斯提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即独立于测量尺度。 对于一个均值为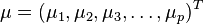 ,协方差矩阵为
,协方差矩阵为 的多变量向量
的多变量向量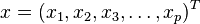 ,其马氏距离为
,其马氏距离为
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为 的随机变量
的随机变量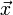 与
与 的差异程度:
的差异程度:
如果协方差矩阵为单位矩阵,马氏距离就简化为欧氏距离;如果协方差矩阵为对角阵,其也可称为正规化的欧氏距离。
其中 是
是 的标准差。
的标准差。
(4)余弦距离 CosineDistanceMeasure
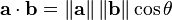
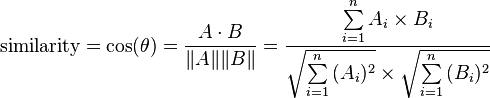
(5)汉明距离
在信息论中,两个等长字符串之间的汉明距离是两个字符串对应位置的不同字符的个数。换句话说,它就是将一个字符串变换成另外一个字符串所需要替换的字符个数。 例如:
10101 与10101 之间的汉明距离是 2。
2396 与2396 之间的汉明距离是 3。
"toned" 与 "roses" 之间的汉明距离是 3。
(6)平方欧几里德距离度量 SquaredEuclideanDistanceMeasure

(7)Tanimoto距离 TanimotoDistanceMeasure

(8)加权距离度量 WeightedDistanceMeasure ,具体实现有:WeightedEuclideanDistanceMeasure和WeightedManhattanDistanceMeasure
用欧几里德距离和曼哈顿距离实现。加权距离度量是Mahout的高级特征,它能让你在不同维上赋予不同的权重,以此对距离度量信息产生影响,WeightedDistanceMeasure在向量格式化中需要序列化为文件。变量对距离的影响是不一样的,通过权值来确定。
(9)切比雪夫距离 ChebyshevDistanceMeasure

Mahout系列之----距离度量的更多相关文章
- Mahout 系列之--canopy 算法
Canopy 算法,流程简单,容易实现,一下是算法 (1)设样本集合为S,确定两个阈值t1和t2,且t1>t2. (2)任取一个样本点p属于S,作为一个Canopy,记为C,从S中移除p. (3 ...
- <转>从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
转自 http://blog.csdn.net/likika2012/article/details/39619687 前两日,在微博上说:“到今天为止,我至少亏欠了3篇文章待写:1.KD树:2.神经 ...
- 从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
转载自:http://blog.csdn.net/v_july_v/article/details/8203674/ 从K近邻算法.距离度量谈到KD树.SIFT+BBF算法 前言 前两日,在微博上说: ...
- ML 07、机器学习中的距离度量
机器学习算法 原理.实现与实践 —— 距离的度量 声明:本篇文章内容大部分转载于July于CSDN的文章:从K近邻算法.距离度量谈到KD树.SIFT+BBF算法,对内容格式与公式进行了重新整理.同时, ...
- 海量数据挖掘MMDS week2: LSH的距离度量方法
http://blog.csdn.net/pipisorry/article/details/48882167 海量数据挖掘Mining Massive Datasets(MMDs) -Jure Le ...
- 距离度量以及python实现(一)
1. 欧氏距离(Euclidean Distance) 欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式. (1)二维平面上两点a(x1,y1)与b(x2,y2)间 ...
- 概率分布之间的距离度量以及python实现(三)
概率分布之间的距离,顾名思义,度量两组样本分布之间的距离 . 1.卡方检验 统计学上的χ2统计量,由于它最初是由英国统计学家Karl Pearson在1900年首次提出的,因此也称之为Pearson ...
- 机器学习方法、距离度量、K_Means
特征向量 1.特征向量:以人为例,每个元素可能就对应这人的某些方面,这就是特征,例如:身高.年龄.性别.国际....2.特征工程:目的就是将现有数据中可作为信号的特征与那些仅是噪声的特征区分开来:当数 ...
- 概率分布之间的距离度量以及python实现
1. 欧氏距离(Euclidean Distance) 欧氏距离是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式.(1)二维平面上两点a(x1,y1)与b(x2,y2)间的欧 ...
随机推荐
- Python 字符串字典内置函数&方法
Python字典包含了以下内置函数: 序号 函数及描述 1 cmp(dict1, dict2)比较两个字典元素. 2 len(dict)计算字典元素个数,即键的总数. 3 str(dict)输出字典可 ...
- Kafka系列之-自定义Producer
前面已经讲到了,在Kafka中,Message是由Producer产生的,Producer产生的Message会发送到Topic的指定Partition中.Producer可以有多种形式,也可以由用户 ...
- Swift运行时简介
因为Swift的操作在高层并且也得与Objc联合起来干活,用Swift写的程序一般会被Objc和Swift运行时处理.因为Swift的本性--换句话说,它是一门静态语言--Swift运行时在一些关键地 ...
- springMVC源码分析--HttpRequestHandlerAdapter(四)
上一篇博客springMVC源码分析--HandlerAdapter(一)中我们主要介绍了一下HandlerAdapter接口相关的内容,实现类及其在DispatcherServlet中执行的顺序,接 ...
- [extjs5学习笔记]第三十七节 Extjs6预览版都有神马新东西
本文在微信公众号文章地址:微信公众号文章地址 本文地址:http://blog.csdn.net/sushengmiyan/article/details/45190485 [TOC] 在Ext JS ...
- static 变量(静态变量)
在C++的面向对象编程中,static还可以加在类的数据成员或成员函数之前.这样定义的数据成员或成员函数就被类所拥有,而不再属于类的对象. #include <iostream> usin ...
- android获取短信并自动填充
package com.velo.quanquan.util; import java.util.regex.Matcher; import java.util.regex.Pattern; impo ...
- JAVA面向对象-----构造方法
我们人出生的时候,有些人一出生之后再起名字的,但是有些人一旦出生就已经起好名字的.那么我们在java里面怎么在对象一旦创建就赋值呢? 构造方法作用 构造方法作用:对对象进行初始化. 构造函数与普通的函 ...
- Linux Debugging (九) 一次生产环境下的“内存泄露”
一个偶然的机会,发现一个进程使用了超过14G的内存.这个进程是一个RPC server,只是作为中转,绝对不应该使用这么多内存的.即使并发量太多,存在内存中的数据太多,那么在并发减少的情况下,这个内存 ...
- Android获得控件在屏幕中的绝对坐标
int[] location = new int[2] ; view.getLocationInWindow(location); //获取在当前窗口内的绝对坐标 view.getLocationOn ...



