BZOJ_1101_[POI2007]Zap_莫比乌斯反演

题意：FGD正在破解一段密码，他需要回答很多类似的问题：对于给定的整数a,b和d，有多少正整数对x,y，满足x<=a
，y<=b，并且gcd(x,y)=d。作为FGD的同学，FGD希望得到你的帮助。

n组询问，（1<=n<= 50000）（1<=d<=a,b<=50000）

分析：

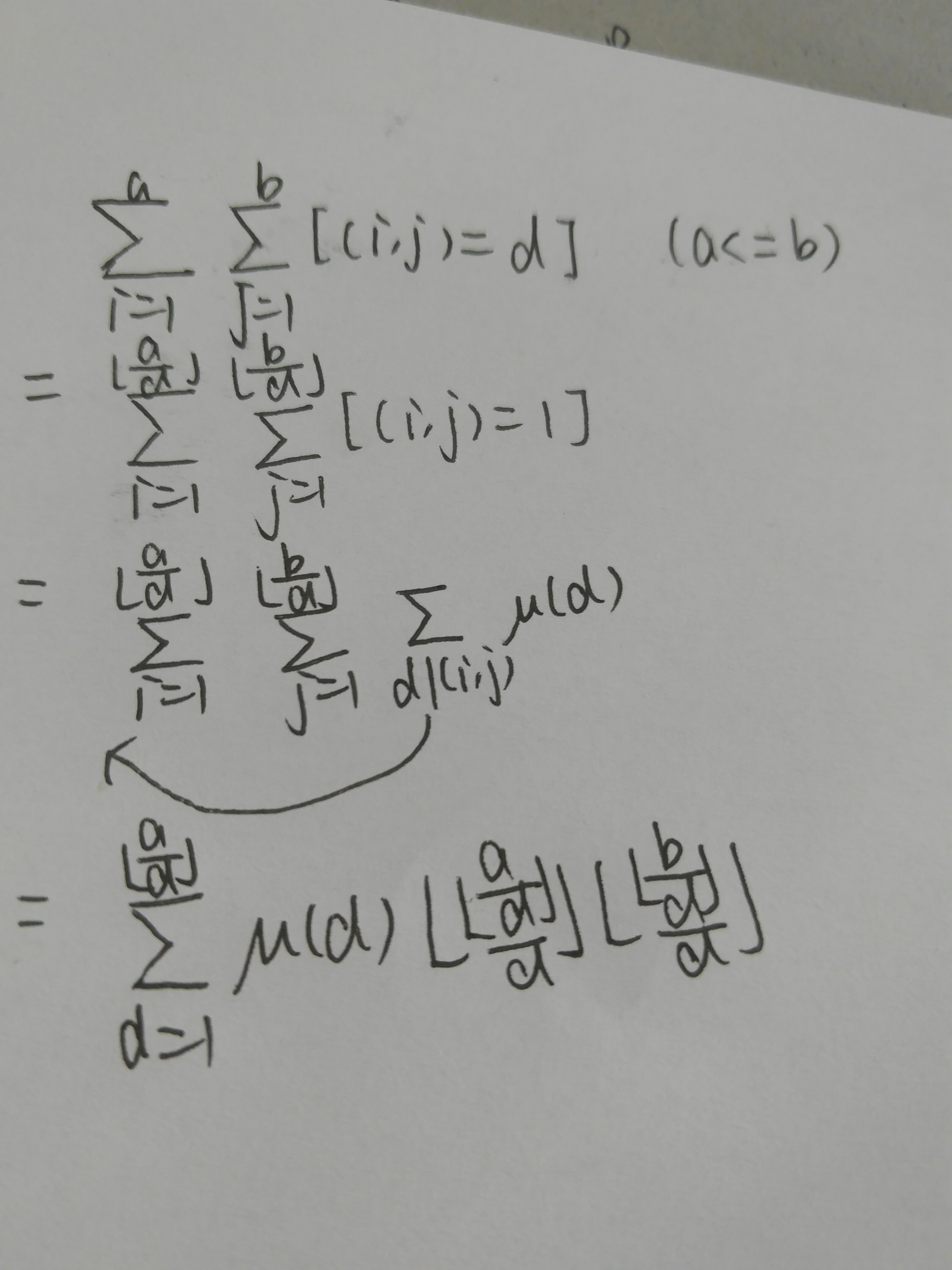
通过处理μ的前缀和把每段$a/i$的值相等的部分一起算。$n/(n/i)$找到值相等的一段的段末位置。

我当时为什么要用图片上传啊。。算了留着吧。

不行还是得补上：

$\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{m}[gcd(i,j)=d]$

$=\sum\limits_{i=1}^{\lfloor \frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}[gcd(i,j)=1]$

$=\sum\limits_{i=1}^{\lfloor \frac{n}{d}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{d}\rfloor}
\sum\limits_{p|(gcd(i,j)}\mu(p)$

$=
\sum\limits_{p=1}^{\lfloor \frac{min(n,m)}{d}\rfloor}\mu(p)\sum\limits_{i=1}^{\lfloor \frac{n}{dp}\rfloor}\sum\limits_{j=1}^{\lfloor\frac{m}{dp}\rfloor}$

$=
\sum\limits_{p=1}^{\lfloor \frac{min(n,m)}{d}\rfloor}\mu(p)s(\lfloor \frac{n}{dp}\rfloor)s(\lfloor \frac{m}{dp}\rfloor)$

代码：

#include <stdio.h>
#include <string.h>
#include <algorithm>
using namespace std;
#define LL long long
int T,a,b,d;
int miu[50050],prime[50050],vis[50050],cnt,msum[50050];
inline void init()
{
    miu[1]=1;
    msum[1]=1;
    for(int i=2;i<=50000;i++)
    {
        if(!vis[i])
        {
            prime[++cnt]=i;
            miu[i]=-1;
        }
        for(int j=1;j<=cnt&&i*prime[j]<=50000;j++)
        {
            vis[i*prime[j]]=1;
            if(i%prime[j]==0)
            {
                miu[i*prime[j]]=0;
                break;
            }
            miu[i*prime[j]]=-miu[i];
        }
        msum[i]=msum[i-1]+miu[i];
    }
}
int main()
{
    init();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d%d%d",&a,&b,&d);
        a=a/d;b=b/d;
        if(a>b)swap(a,b);
        int lst;
        LL ans=0;
        for(int i=1;i<=a;i=lst+1)
        {
            lst=min(a/(a/i),b/(b/i));
            ans+=1ll*(msum[lst]-msum[i-1])*(a/i)*(b/i);
        }
        printf("%lld\n",ans);
    }
}