遗传算法:N皇后
N皇后问题描述
N皇后问题是一个经典的问题,在一个N*N的棋盘上放置N个皇后,每行一个并使其不能互相攻击(同一行、同一列、同一斜线上的皇后都会自动攻击)。

遗传算法
遗传算法是局部束搜索的变形: 与自然选择过程相似,通过把两个父代结合产生后继(有性繁殖),而不是修改单一状态(无性繁殖)。
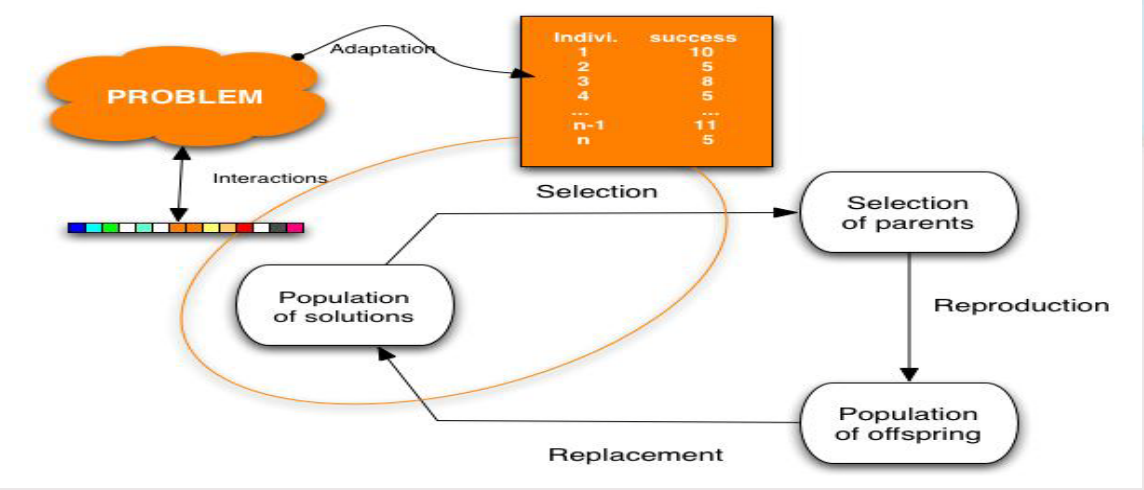
1、通过结合两个状态来产生后继状态
2、从k个随机产生的状态开始(种群)
3、状态表示成字符串(染色体)
4、评估函数(适应值函数)
5、通过选择(轮盘赌选择法)、交叉(杂交)和变异操作来产生新一代种群
6、半性繁殖的局部束搜索
7、适应值函数:相互攻击不到的皇后对数
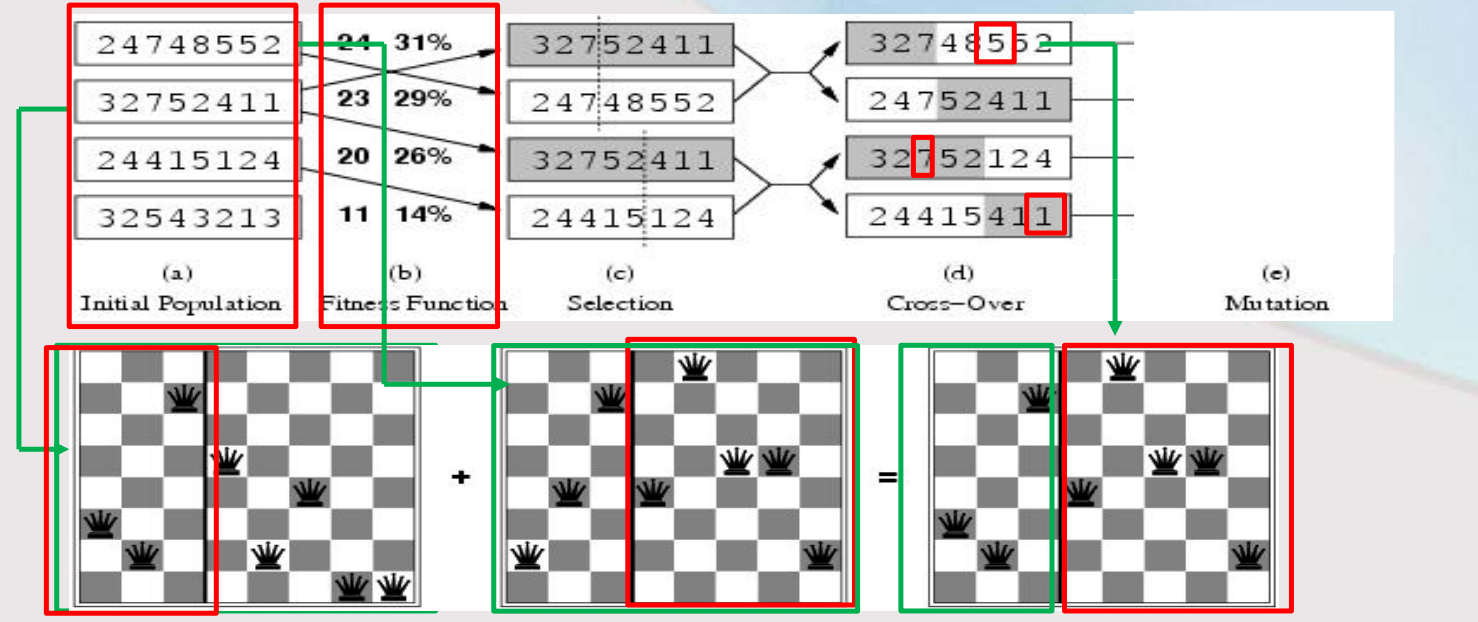
轮盘赌选择法
轮盘赌选择法是依据个体的适应度值计算每个个体在子代中出现的概率,并按照此概率随机选择个体构成子代种群。轮盘赌选择策略的出发点是适应度值越好的个体被选择的概率越大。因此,在求解最大化问题的时候,我们可以直接采用适应度值来进行选择。但是在求解最小化问题的时候,我们必须首先将问题的适应度函数进行转换,以将问题转化为最大化问题。下面给出最大化问题求解中遗传算法轮盘赌选择策略的一般步骤:
(1) 将种群中个体的适应度值叠加,得到总适应度值==1 ,其中 为种群中个体个数。
(2) 每个个体的适应度值除以总适应度值得到个体被选择的概率
(3) 计算个体的累积概率以构造一个轮盘。
(4) 轮盘选择:产生一个[0,1]区间内的随机数,若该随机数小于或等于个体的累积概率且大于个体1的累积概率,选择个体进入子代种群。
重复步骤(4)次,得到的个体构成新一代种群。
图 3.4 染色体的轮盘赌式选择
伪代码:
//主循环
void Genetic::GeneticAlgorithm()
while m_NotSuccess为真
Select
Crossover
Mutate
End while
打印最优解
End
//计算一个state(棋盘)的适应值
//适应值采用“互相攻击皇后对的个数的倒数”,这比书上直接计算不互相攻击的皇后对数作为适应值的方法相比,更能拉开不同状态之间的差距。
//@para state:一个状态的引用
double Genetic::CalcuAdaptive(vector &state)
counter←0
For i: 0 to QueenNum-1 do
For i: 0 to QueenNum-1 do
If 对角线方向互相攻击,或者垂直方向互相攻击
counter++
End if
End for
End for
If counter等于0
m_NotSucess←false,程序的循环终止条件
m_BestOne←state,保存当前的状态
End if
Return 1.0/counter
End
//自然选择,大体思路是轮盘赌选择
void Genetic::Select()
创建一个新的空种群newPopulation
For i: 1 to populationSize-1 do
m_accumuAdaptive[i]←m_accumuAdaptive[i - 1] + m_adaptive[i]
End for
totalAdaptive←m_accumuAdaptive的最后一个元素
For i: 0 to populationSize-1 do
先把totalAdaptive(这是一个实数)放大成一个整数
产生一个随机数 ,对totalAdaptive求模,得到 ran
按相同比例缩小成一个实数
用二分查找的方法,在m_ accumuAdaptive内进行查找 ran,找出位置 j
把m_population的第 j 个状态push_back到newPopulation中
End for
m_population←newPopulation
End
杂交有多种思路:
- 选择两个state状态,随机产生一个杂交点,然后对这个杂交点的右(左)边的“基因”进行交换
- 选择两个state状态,随机产生一个杂交点,然后再对这个杂交点两边的“基因”都进行交换。
- 选择两个state状态,随机产生两个杂交点,然后再对这两个杂交点之间的“基因”进行交换。
变异:
通过伪随机数,使每一个基因有0.0几的概率进行突变。突变就是用伪随机数赋值。
代码实现
Genetic.h
#pragma once
#include <iostream>
#include <cstdlib>
#include <iomanip>
#include <algorithm>
#include <vector>
#include <ctime>
#include <cmath>
#include <fstream>
using namespace std; class Genetic {
private:
int m_Num; // 皇后数量
bool m_IsSuccess; // 是否成功找到最优解
vector<int>m_optimalSolution; // 最优解.
vector<vector<int> >m_population; // 种群
vector<double>m_adaptive; // 种群的适应值(1/冲突数)。
vector<double>m_AdaptValue; // 累积的适应值(定位哪一个被选中的) public:
Genetic(int numOfQueens, int initialGroupNum);
double CalcuAdaptive(vector<int> &state); // 计算适应值(互不相攻击的皇后对数)
void SetPopulation();
void Choose(); // 选择
void GeneticCrossover(); // 杂交
void GeneticMutate(); // 变异
void GeneticCalculation();
void Print(); // 打印最优解
};
Genetic.cpp
Genetic::Genetic(int numOfQueens, int initialGroupNum) {
m_adaptive.resize(initialGroupNum, );
m_AdaptValue.resize(initialGroupNum, );
m_Num = numOfQueens;
m_IsSuccess = true;
SetPopulation();
}
void Genetic::SetPopulation() {
m_population.clear();
vector<int> tmpState(m_Num, );
for (int i = ; i < m_adaptive.size(); ++i) {
for (int j = ; j < m_Num; ++j) // 初始化
tmpState[j] = rand() % m_Num;
m_population.push_back(tmpState);
m_adaptive[i] = CalcuAdaptive(tmpState);
}
}
double Genetic::CalcuAdaptive(vector<int> &state) {
int conflict = ;
for (int i = ; i < m_Num; ++i) {
for (int j = i + ; j < m_Num; ++j) {
//如果对角线方向互相攻击,或者垂直方向互相攻击
if (state[i] == state[j] || abs(state[i] - state[j]) == j - i)
conflict++;
}
}
if (conflict == ) { // 找到最优解
m_IsSuccess = false;
m_optimalSolution = state; //保存当前的状态
}
return 1.0 / conflict;
}
//自然选择(大体思路是轮盘赌选择)
void Genetic::Choose() {
vector<vector<int>> NewPopulation; //创建一个新的空种群NewPopulation
m_AdaptValue[] = m_adaptive[];
for (int i = ; i < m_AdaptValue.size(); i++)
m_AdaptValue[i] = m_AdaptValue[i - ] + m_adaptive[i];
double totalAdaptive = m_AdaptValue[m_AdaptValue.size() - ];
//避免陷入局部最优解(不直接选择适应值最高的两个进行杂交)
for (int i = ; i < m_population.size(); i++) {
//比例缩放的轮盘赌
int magnifyTotalAdaptive = totalAdaptive * ; //实数->整数(放大)
int random = (rand()*rand()) % magnifyTotalAdaptive;//转动轮盘
double select = (double)random / ; //按相同比例缩小
//int select = rand()*rand() % ((int)totalAdaptive);
vector<double>::iterator indexi;
//二分查找: 在m_AdaptValue中查找适应值与select最接近的个体的下标
indexi = lower_bound(m_AdaptValue.begin(), m_AdaptValue.end(), select);
int indexj = indexi - m_AdaptValue.begin();
//加入新的种群中
NewPopulation.push_back(m_population[indexj]);
}
// 更新种群
m_population.clear();
m_population = NewPopulation;
}
void Genetic::GeneticCrossover() { //杂交==>交换基因片段(皇后位置进行交换)
int first = ;
int row1;
for (int i = ; i < m_population.size(); i++) {
if (rand() % ) {
++first;
if (first % == ) {
int crossPoint = rand() % (m_Num - );
for (int j = crossPoint; j < m_Num; j++)swap(m_population[row1][j], m_population[i][j]); //值交换
}
else row1 = i;
}
}
}
void Genetic::Print() {
for (int i = ; i < m_optimalSolution.size(); ++i) {
for (int j = ; j < m_optimalSolution.size(); ++j) {
if (j == m_optimalSolution[i]) cout << "Q ";
else cout << ". ";
}cout << '\n';
}cout << '\n';
}
//随机突变=> 随机改变某个个体的某个基因(随机改变某个地图中的某个皇后的位置)
void Genetic::GeneticMutate() {
int mutateSpot = ;
for (int i = ; i < m_population.size(); ++i) {
if (rand() % == ) {
mutateSpot = rand() % m_Num;
m_population[i][mutateSpot] = rand() % m_Num;
}
m_adaptive[i] = CalcuAdaptive(m_population[i]); // 更新适应值
}
}
void Genetic::GeneticCalculation() {
clock_t start, finish;
start = clock();
while (m_IsSuccess) {
// 自然选择
Choose();
// 杂交
GeneticCrossover();
// 变异
GeneticMutate();
}
//打印最优解
//if (m_Num<25) Print();
Print();
finish = clock();
cout << "遗传算法求解时间: " << finish - start << "ms" << endl;
}
main.cpp
#include"Genetic.h"
int main() {
int numOfQueen;
cout << "请输入皇后数目: ";
cin >> numOfQueen;
cout << "【遗传算法求解】" << endl;
Genetic Q(numOfQueen, );
Q.GeneticCalculation();
system("pause");
}
运行结果:
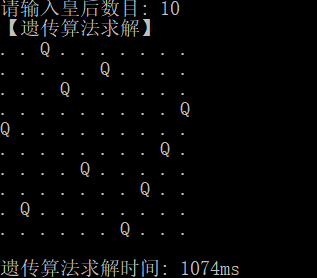
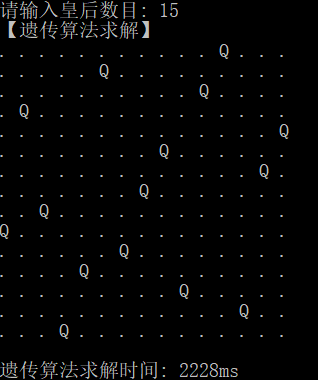
遗传算法:N皇后的更多相关文章
- 简单遗传算法求解n皇后问题
版权声明:本文为博主原创文章,转载请注明出处. 先解释下什么是8皇后问题:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行.同一列或同一斜线上,问有多少种摆法.在不 ...
- 【译】N 皇后问题 – 构造法原理与证明 时间复杂度O(1)
[原] E.J.Hoffman; J.C.Loessi; R.C.Moore The Johns Hopkins University Applied Physics Laboratory *[译]* ...
- 递归实现n(经典的8皇后问题)皇后的问题
问题描述:八皇后问题是一个以国际象棋为背景的问题:如何能够在8×8的国际象棋棋盘上放置八个皇后, 使得任何一个皇后都无法直接吃掉其他的皇后?为了达到此目的,任两个皇后都不能处于同一条横行.纵行或斜线上 ...
- 八皇后算法的另一种实现(c#版本)
八皇后: 八皇后问题,是一个古老而著名的问题,是回溯算法的典型案例.该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于 ...
- [LeetCode] N-Queens II N皇后问题之二
Follow up for N-Queens problem. Now, instead outputting board configurations, return the total numbe ...
- [LeetCode] N-Queens N皇后问题
The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens ...
- N皇后问题—初级回溯
N皇后问题,最基础的回溯问题之一,题意简单N*N的正方形格子上放置N个皇后,任意两个皇后不能出现在同一条直线或者斜线上,求不同N对应的解. 提要:N>13时,数量庞大,初级回溯只能保证在N< ...
- 用遗传算法GA改进CloudSim自带的资源调度策略(2)
遗传算法GA的核心代码实现: 最核心: private static ArrayList<int[]> GA(ArrayList<int[]> pop,int gmax,dou ...
- 用遗传算法GA改进CloudSim自带的资源调度策略
首先理解云计算里,资源调度的含义: 看了很多云计算资源调度和任务调度方面的论文,发现很多情况下这两者的意义是相同的,不知道这两者是同一件事的不同表述还是我没分清吧,任务调度或者资源调度大概就是讲这样一 ...
随机推荐
- SQL SERVER 字符串按数字排序
需求是这样的: 数据库表里面有一个字段类型是nvachar,存的值是数字和字符混合的,要实现先按数字排序,再按字母倒序. 思路: 考虑这个字段的值是否是有规律可循的,把要按数字排序的部分转换为数字,再 ...
- @SpringBootApplication 组合注解包含哪些注解及作用
序:在学习springboot,教程一般对一些注解语焉不详,发现@SpringBootApplication 这个注解包含了很多注解,也就是说使用这个注解可以少写几个注解,这里看源码粘出来一些,仅用于 ...
- Hadoop学习笔记一(HDFS架构)
介绍 Hadoop分布式文件系统(HDFS)设计的运行环境是商用的硬件系统.他和现存的其他分布式文件系统存在很多相似点.不过HDFS和其他分布式文件系统的区别才是他的最大亮点,HDFS具有高容错的特性 ...
- Vue2学习小记-给Vue2路由导航钩子和axios拦截器做个封装
1.写在前面 最近在学习Vue2,遇到有些页面请求数据需要用户登录权限.服务器响应不符预期的问题,但是总不能每个页面都做单独处理吧,于是想到axios提供了拦截器这个好东西,再于是就出现了本文. 2. ...
- 开源软件:NoSql数据库 - 图数据库 Cassandra
转载原文:http://www.cnblogs.com/loveis715/p/5299495.html Cassandra简介 在前面的一篇文章<图形数据库Neo4J简介>中,我们介绍了 ...
- python入门(14)定义函数和接收返回值
定义函数: 定义一个求绝对值的my_abs函数为例: def my_abs(x): if x >= 0: return x else: return -x 如果没有return语句,函数执行完毕 ...
- Hibernate(十六):Hibernate二级缓存
Hibernate缓存 缓存(Cache):计算机领域非常通用的概念.它介于应用程序和永久性数据存储源(如磁盘上的文件或者数据库)之间,起作用是降低应用程序直接读取永久性数据存储源的频率,从而提高应用 ...
- QT生成随机数
QT生成随机数和C语言差距不大,C语言用srand()和rand(),QT是用Qsrand()和qrand(): QT生成随机数的格式是: qsrand(QTime(0,0,0).secsTo(QTi ...
- 元组tuple插入字符串的方式
元组无法更改,但是可以用切片的方式将头尾切出,中间'+'字符串,后整体赋值原先的元组,举例如下 >>> temp=('东邪','西毒' ,'南帝') >>> tem ...
- C++_进阶之函数模板_类模板
C++_进阶之函数模板_类模板 第一部分 前言 c++提供了函数模板(function template.)所谓函数模板,实际上是建立一个通用函数,其函数类型和形参类型不具体制定,用一个虚拟的类型来 ...

