斯坦福大学公开课机器学习：advice for applying machine learning | model selection and training/validation/test sets（模型选择以及训练集、交叉验证集和测试集的概念）

怎样选用正确的特征构造学习算法或者如何选择学习算法中的正则化参数lambda？这些问题我们称之为模型选择问题。 在对于这一问题的讨论中,我们不仅将数据分为：训练集和测试集，而是将数据分为三个数据组：也就是训练集、验证集和测试集。本节将会介绍这些内容的含义，以及如何使用它们进行模型选择。在前面的学习中，我们已经多次接触到过拟合现象。在过拟合的情况中学习算法在适用于训练集时表现非常完美，但这并不代表此时的假设也很完美（如下图）。

更普遍地说，过拟合是训练集误差通常不能正确预测出该假设是否能很好地拟合新样本的原因。具体来讲，如果把这些参数集，比如theta1、theta2等，调整到非常拟合我们的训练集。那么结果就是我们的假设会在训练集上表现地很好。但这并不能确定当我们的假设推广到训练集之外的新的样本上时, 预测的结果是怎样的。而更为普遍的规律是只要我们的参数非常拟合某个数据组。比如说非常拟合训练集，当然也可以是其他数据集。那么我们的假设对于相同数据组的预测其预测误差，比如说训练误差，是不能够用来推广到一般情况的，或者说是不能作为实际的泛化误差的。也就是说，不能说明我们的假设对于新样本的效果。下面我们来解释模型选择问题。假如说我们现在要选择能最好地拟合数据的多项式次数。换句话说，我们应该选择一次函数、二次函数还是三次函数呢？或者一直到十次函数？所以似乎在这个算法里应该有这样一个参数，这里我们用d来表示我们应该选择的多项式次数。所以，我们除了要考虑确定的参数theta之外，还要考虑一个参数——多项式的次数d。当d=1时，表示线性(一次)方程。以此类推，如下图。

因此，我们想确定这个多出来的参数d最适当的取值。具体地说，比如我们想要选择一个模型，那就从这10个模型中选择一个最适当的多项式次数，并且用这个模型进行估测，预测我们的假设能否很好地推广到新的样本上。那么我们可以这样做，先选择第一个模型（d=1），然后求训练误差的最小值，这样就会得到一个参数向量theta，然后再选择第二个模型——二次函数模型，进行同样的过程这样得到另一个参数向量theta。为了区别这些不同的参数向量theta，用上标（1）、（2）来表示，这里的上标(1)表示的是在调整第一个模型使其拟合训练数据时得到的参数theta。同样地，theta上标(2)表示的是二次函数在和训练数据拟合的过程中得到的参数，以此类推。在拟合三次函数模型时又得到一个参数theta(3)等等，直到theta（10）。

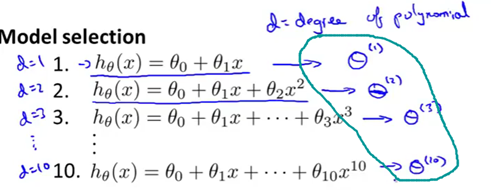
接下来我们要做的是对所有这些模型求出测试集误差。因此，我可以算出Jtest(θ(1))、Jtest(θ(2))，等等。也就是对于每一个模型对应的假设，其作用于测试集的表现如何。接下来为了确定选择哪一个模型最好，我们要做的是：假设一个例子最终选择了五次多项式模型。现在我们想知道这个模型能不能推广到新的样本，我们可以观察这个五次多项式假设模型对测试集的拟合情况。但有一个问题是这样做仍然不能公平地说明我的假设推广到一般时的效果。其原因在于我们选择了一个能够最好地拟合测试集的参数d的值及多项式的度。即我们选择了一个能够最好地拟合测试集的参数d的值。因此，我们的参数向量theta(5)在拟合测试集时的结果，也就是对测试样本预测误差时，很可能导致一个比实际泛化误差更完美的预测结果。因为我们找了一个最能拟合测试集的参数d，因此我们再用测试集来评价我们的假设时，就显得不公平了。因为我们选择的多项式次数d本身就是按照最拟合测试集来选择的，因此我们的假设很可能很好地拟合测试集而且这种拟合的效果很可能会比那些没见过的新样本拟合得更好。但我们更关心对新样本的拟合效果的。

为了调整这个评价假设时模型选择的问题，我们通常会采用如下的方法来解决。我们不要将数据集仅仅分为训练集和测试集两部分，而是分割为三个部分。第一部分和之前一样,也是训练集。那么我们把第一部分还是称为训练集，然后第二部分数据，我们将其称为交叉验证集（cross validation，CV）。有时也把交叉验证直接称为验证集。最后部分数据称之为测试集。最典型的分配三组数据比例是：将整个数据的60%分给训练集，然后20%作为验证集，20%作为测试集。当然这些比值可以稍微进行调整，但这种分法是最典型的比例。交叉验证集或者叫验证集，就会有某个数量的样本，用m下标cv来表示这个数量，因此它表示的是交叉验证样本的总数。沿用之前使用的标记法则，使用(x(i)cv，y(i)cv) 来表示交叉验证样本。用m下标test来表示测试样本的总数。这样就定义了训练集或交叉验证和以及测试集。

同样地我们可以定义训练误差、交叉验证误差和测试误差。训练误差可以这样定义，我将训练误差写作J下标train(θ)。和前面完全是一个意思，这就是我们通常写的J(θ)。这是当我们对训练集进行预测时，得到的训练集误差。然后J下标cv表示的是验证集误差，就像训练集误差一样，只不过是对验证样本进行预测得到的结果而已。另外测试误差也是一样的。在考虑像这样的模型选择问题时，我们不再使用测试集来进行模型选择。取而代之的是使用验证集，也叫交叉验证集来选择模型。具体来讲，我们首先要选取第一种假设，或者说第一个模型，使得代价函数取最小值。这样我们可以得到对应一次模型的一个参数向量theta，然后像之前一样，我们也用上标（1）来表示它是一次模型的参数。我们再对二次函数模型进行同样的步骤，这样我们又得到一个参数向量theta（2）。然后是theta(3)，等等。一直到多项式次数为10的情况。接下来的做法，与之前不同的是，我们不是使用测试集来测试这些假设的表现如何，而是使用交叉验证集来测试其预测效果。因此我们要对每一个模型都算出其对应的Jcv，来观察这些假设模型中，哪一个能最好地对交叉验证集进行预测。我将选择交叉验证误差最小的那一组假设作为我们的模型。对于这个例子，为了讨论方便，我们假设四次多项式，对应的交叉验证误差最小。那么在这种情况下，我们就选择四次多项式模型作为我们最终的选择。这表示的是参数d（多项式次数），我们选择了最合适的d=4。我们是使用交叉验证集来确定的这个参数。这样我们就为测试集留出了一条路，现在我们就能使用测试集来预测或者估计，通过学习算法得出的模型的泛化误差了。

最后要说明的一点是在如今的机器学习应用中，很少有人按照前面介绍的那个步骤做的，就像我们前面说过的（使用测试集来做模型选择，然后再使用同样的测试集，来测出误差，评价假设的预测效果）。这实在不是一个好主意，用测试集来选择模型，然后使用相同的测试集来报告误差。通过使用测试集来选择多项式的次数，然后求测试集的预测误差，尽管这样做的确能得到一个很理想的泛化误差。如果你有一个很大很大的测试集，也许情况稍微好些，但大多数的机器学习，实践者一般还是建议最好不要这样做。最好还是分成训练集、验证集和测试集。