BP算法的矩阵推导

目录

• 1. 需要的微积分知识
  • 1.1 导数
  • 1.2 求导的链式法则
• 2. 梯度下降法
  • 2.1 梯度
  • 2.2 梯度算法的解释
• 3.误差反向传播算法
  • 3.1 理论推导
    • 3.1.1 符号说明
    • 3.1.2 推导过程
  • 3.2 BP算法的小结
  • 3.3 Python实现
    • 3.3.1 最简单三层网络
  • 3.4 附录：

1. 需要的微积分知识

1.1 导数

对于一元函数，在导数存在的情况下，在某一点的导数，也就是该点的斜率。
对于多元函数，对于某一点求导，则需要指明方向，两个特殊的方向，1. 偏导：在坐标轴方向的导数 2. 梯度的方向:总有一个方向是变化最快的。

1.2 求导的链式法则

1. \(x \in R\), \(z=g(f(x))\), \(y=f(x)\)
   \[ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y} \frac{\partial y}{\partial x}\]
2. $ x \in R^m $, \(f(x)\)是\(R^M\)到\(R^n\)的映射，\(g(f)\)是\(R^n\)到R的映射
   \[ \frac{\partial g}{\partial x_i}=\sum_j^n \frac{\partial g}{\partial f_i} \frac{\partial f_i}{\partial x_i}\]
   如果使用向量表示
   \[ \nabla_x^z=(\frac{\partial f}{\partial x})^T \nabla_y^z\]

2. 梯度下降法

2.1 梯度

梯度其实本质也是一个向量，对于函数\(f(X,y)\)
在\((W,y)\)这一点的梯度 $ (\frac{\partial f}{\partial X},\frac{\partial f}{\partial y})$
梯度的几何意义：在该点变化增加最快的地方

2.2 梯度算法的解释

图来自吴恩达的机器学习课程

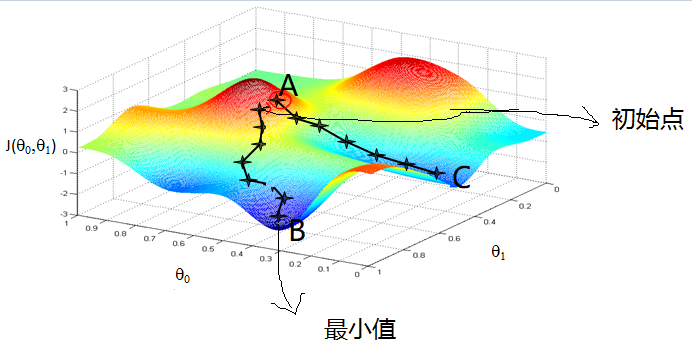
颜色偏红(A)的地方开始，根据梯度的负方向通过9次更新，达到了最小值(B)。
现在给定一个点\(A(\theta_0,\theta_1)\),干嘛呢，我们想从A到B点（最小值点),类似人类下山，需要知道往那个方向吧、走大多一步呢？
方向：梯度的负方向 \(\delta=(\frac{\partial L}{\partial \theta_0},\frac{\partial L}{\partial \theta_1}))\)
步长：学习率（\(\alpha\))
因此，计算一次里目标更近了 \((\theta_0,\theta_1)=(\theta_0,\theta_1)-\alpha \dot (\delta)\)
在重复上两步，直到满意为止。

3.误差反向传播算法

3.1 理论推导

3.1.1 符号说明

上图是一个L层的神经网络，输入层为第一层，隐藏层：2至\(L-1\)层，输出层L

令 输入向量 \(\vec{X}\)
\[ \vec{X} = (x_1,x_2,...,x_{m-1},x_m)\]
输出向量 \(\vec{Y}\)
\[ \vec{Y}=(y_1,y_2,...,y_{n-1},y_n)\]
第j层隐藏层的输出向量 \(\vec{h^{(j)}}\)
\[\vec{h^{(j)}}=(h_1^{(j)},h_2^{{j}},...,h_{t-1}^{(j)},h_tj^{(j)})\]
其中，\(tj\):表示第j的隐藏层个数
第\((l-1)\)层的第i个神经元到第\(l\)层的第j个神经元的连接权重：\(w_{ij}^{(l)}\)，则第\((l-1)\)层神经元到第\(l\)层神经元的连接权重矩阵

\[W^{(l)}=\left( \begin{matrix}w_{11}^{(l)}& \cdots & w_{1(tj)}\\
& \dots &\\
w_{s(l-1)}^{l}&\cdots&w_{s(l-1)s(l)}^{l}
\end{matrix}\right)\]

3.1.2 推导过程

3.1.2.1 误差

定义的误差函数,常见的衡量性指标见 戳我,这里选择的误差平方和最小
第\(i\)个输出的误差,假设实际输出\((d(1),d(2),...,d(n))\)：,一个输入样本对应的误差
\[E(i)=\frac{1}{2}\sum_{k=1}^n(y(i)-d(i))^2=\frac{1}{2}||y-d||^2\]

所有训练样本(\(N\))的误差：
\[E(i)=\frac{1}{2}\sum_{j=1}^{N}(\sum_{k=1}^n(y(i)-d(i))^2)=\frac{1}{2N}\sum_{j=1}^{N}(||y(i)-d(i)||^2)\]

因此，
\[ E = \frac{1}{2N}\sum_{i=1}^N(||y(i)-d(i)||^2)\]
其实，神经网络的输出是关于节点的复合函数。代价函数是关于\(W\)和\(b\)的函数。

3.1.2.2 正向传播

输入层\(\hat{X}\)：
\[ X =(x_1,x_2,x_3,...,x_m)\]
当有\(N\)个训练样本时，可用矩阵表示

\[ X=\left( \begin{matrix}
x_{11} &x_{12}&...&x_{1m}\\
x_{21} & x_{22}&...&x_{2m}\\
\vdots & \vdots&\dots&\vdots\\
x_{N1} & \vdots&\vdots&x_{Nm}\\
\end{matrix} \right)\]

第二层 \(h^{(2)}\),一共\(s2\)个节点:
第i个节点的计算
\[h^{(2)}(i)=f(\sum_{j=1}^{s2}x(j)*w_{ji}^{(l)}+b_i)=f(x*w(:,i)+b_i)\]
矩阵表示
\[ h^{(2)}=f(x*W^{(l)}+b^{(2)})\]
第i层 矩阵形式
\[ h^{(l)}=f(h^{(l-1)}*W^{(l)}+b)\]

3.1.2.3 反向传播

梯度下降法更新权重，不断迭代到最优解。
对\(w_{ij}\)求导数可得,可更新\(w_{ij}\)更新公式：
\[ w_{ij}=w_{ij}-\alpha \frac{\partial E}{\partial w_{ij}}\]
当然简单的情况下，可直接写出公式，当太复杂的时候，引入BP简化求导

方便书写公式，对于第i的输入\(h^{(i-1)}*W^{(i)}+b^{(i)}\)记作\(net^{(i)}\),其中，第\(i\)的输入和输出的关系，\(输入=f(输出)\)
下面开始推导

首先，对于\(L\)层，

对于\(W^{(L)}\)，先看对\(W_{ij}^{(L)}\)求导，
\[ \frac{\partial E}{\partial W_{ij}^{(L)}}
=\frac{\partial E}{\partial y(j)} * \frac{\partial y(i)}{\partial net_{j}^{L}} * \frac{\partial net_{j}^{L}}{\partial W_{ij}^{(L)}}\\
=(y(j)-d(j))*f(x)^{'}|_{x=net_j^{(L)}}h_i^{(L-1)}\]

令\(\delta_i^{(L)}=y(i)-d(i)\)

上述给出了单个分量的求偏导的结果，对于\(W^{(L)}\)
\[
\frac{\partial E}{\partial W^{(L)}}
=\left[\begin{matrix}
\frac{\partial E}{\partial W_{11}^{(L)}} & \frac{\partial E}{\partial W_{12}^{(L)}}&\dots & \frac{\partial E}{\partial W_{1n}^{(L)}}\\
\frac{\partial E}{\partial W_{21}^{(L)}} & \frac{\partial E}{\partial W_{22}^{(L)}}&\dots& \frac{\partial E}{\partial W_{2n}^{(L)}}\\
\vdots& \dots& \dots& \dots\\
\frac{\partial E}{\partial W_{sL,1}^{(L)}} & \frac{\partial E}{\partial W_{sL,2}^{(L)}}&\dots& \frac{\partial E}{\partial W_{sL,n}^{(L)}}
\end{matrix}\right]
\\= \left[
\begin{matrix}
h^{(L-1)}_1\\h^{(L-1)}_2\\ \dots\\h^{(L-1)}_n
\end{matrix}
\right] *\left[\begin{matrix}
\delta_1^{(L)}f(x)^{'}|_{x=net_1^{(L)}}\\
\delta_2^{(L)}f(x)^{'}|_{x=net_2^{(L)}}\\
\dots\\
\delta_n^{(L)}f(x)^{'}|_{x=net_n^{(L)}}
\end{matrix}\right] ^T
=h^{(L-1)}S^{(L)}
\]
其中，
\[
S^{(L)}=\left[\begin{matrix}
\delta_1^{(L)}f(x)^{'}|_{x=net_1^{(L)}}\\
\delta_2^{(L)}f(x)^{'}|_{x=net_2^{(L)}}\\
\dots\\
\delta_n^{(L)}f(x)^{'}|_{x=net_n^{(L)}}
\end{matrix}\right]^T
\]
同理可得，
\[
\frac{\partial E}{\partial b_k^{(L)}}=(y(j)-d(j))*f(x)^{'}|_{x=net_j^{(L)}}
\]
其次，对于隐含层\(L-1\)层，对\(W_{ij}^{(L)}\)求导
\[
\frac{\partial E}{\partial W_{ij}^{(L-1)}}
=\sum_{k=1}^{n}\frac{\partial E}{\partial y(k)} * \frac{\partial y(k)}{\partial net_{k}^{L}} * \frac{\partial net_{k}^{L}}{\partial f(net_j^{(L-1)})}*\frac{\partial f(net_j^{(L-1)})}{\partial net_j^{(L-1)}}*\frac{\partial net_j^{(L-1)}}{\partial W_{ij}^{(L-1)}}\\
=\sum_{k=1}^{n} (y(j)-d(j))*f(x)^{'}|_{x=net_j^{(L)}}W_{kj}^{(L)}f(x)^{'}|_{x=net_j^{L-1}}h_i^{L-2}\\
=\sum_{k=1}^{n}S_i^{(L)}W_{kj}^{(L)}f(x)^{'}|_{x=net_j^{L-1}}h_i^{L-2}\\
\]

写出矩阵形式,对\(W^{(L-1)}\)

\[
\frac{\partial E}{\partial W^{(L-1)}}=\left[\begin{matrix} h^{(L-2)}_1\\h^{(L-2)}_2\\\vdots\\h^{(L-2)}_{s(L-2)}\end{matrix}\right] \left[\begin{matrix}
\delta_1^{(L)}f(x)^{'}|_{x=net_1^{(L)}}\\
\delta_2^{(L)}f(x)^{'}|_{x=net_2^{(L)}}\\
\dots\\
\delta_n^{(L)}f(x)^{'}|_{x=net_n^{(L)}}
\end{matrix}\right]^T
\left[\begin{matrix}
W_{11}^{(L)} & W_{12}^{(L)}&\dots & W_{1n}^{(L)}\\
W_{21}^{(L)} & W_{22}^{(L)}&\dots& W_{2n}^{(L)}\\
\vdots& \dots& \dots& \dots\\
W_{s(L-1),1}^{(L)} & W_{s(L-1),2}^{(L)}&\dots& W_{s(L-1),n}^{(L)}
\end{matrix}\right]^T
\\
\left[ \begin{array}{ccc}{f^{'(L-1)}\left(net^{(L-1)}_{(1)}\right)} & {0} & {0}&{0} \\ {0} & {f^{'(L-1)}\left(net^{(L-1)}_{(2)}\right)} & {0} &{0}\\
0 & \dots & \vdots & 0\\{0} & {0} & {0}&{f^{(L-1)}\left(ne t_{s(L-1)}^{(L-1)}\right)}\end{array}\right]\\
=h^{(L-2)}S^{(L-1)}
\]

\[
S^{(L-1)}=\left(\left[\begin{matrix}
f(x)^{'(L)}|_{x=net_1^{(L)}}&0& \dots& 0\\
0&f(x)^{'}|_{x=net_2^{(L)}}0& \dots& 0\\
0&\dots&\dots&0\\
0&0&0&f(x)^{'(L)}|_{x=net_n^{(L)}}
\end{matrix}\right]\left[\begin{matrix} \delta_1^{(L)}\\\delta_2^{(L)}\\\vdots\\\delta_n^{(L)}\end{matrix}\right] \right)^T\\
\left[\begin{matrix}
W_{11}^{(L)} & W_{12}^{(L)}&\dots & W_{1n}^{(L)}\\
W_{21}^{(L)} & W_{22}^{(L)}&\dots& W_{2n}^{(L)}\\
\vdots& \dots& \dots& \dots\\
W_{s(L-1),1}^{(L)} & W_{s(L-1),2}^{(L)}&\dots& W_{s(L-1),n}^{(L)}*
\end{matrix}\right]^T
\left[ \begin{array}{ccc}{f^{'(L-1)}\left(net^{(L-1)}_{(1)}\right)} & {0} & {0}&{0} \\ {0} & {f^{'(L-1)}\left(net^{(L-1)}_{(2)}\right)} & {0} &{0}\\
0 & \dots & \vdots & 0\\{0} & {0} & {0}&{f^{(L-1)}\left(ne t_{s(L-1)}^{(L-1)}\right)}\end{array}\right]\\
=S^{(L)}\left[\begin{matrix}
W_{11}^{(L)} & W_{12}^{(L)}&\dots & W_{1n}^{(L)}\\
W_{21}^{(L)} & W_{22}^{(L)}&\dots& W_{2n}^{(L)}\\
\vdots& \dots& \dots& \dots\\
W_{s(L-1),1}^{(L)} & W_{s(L-1),2}^{(L)}&\dots& W_{s(L-1),n}^{(L)}*
\end{matrix}\right]^T\left[ \begin{array}{ccc}{f^{'(L-1)}\left(net^{(L-1)}_{(1)}\right)} & {0} & {0}&{0} \\ {0} & {f^{'(L-1)}\left(net^{(L-1)}_{(2)}\right)} & {0} &{0}\\
0 & \dots & \vdots & 0\\{0} & {0} & {0}&{f^{(L-1)}\left(ne t_{s(L-1)}^{(L-1)}\right)}\end{array}\right]*\\
\]

对\(1<l<L\),求\(W^{(l)}\)的偏导,

最后，根据上述的推导喔，很容易得出\(S^{(l)}\)和\(S^{(l+1)}\),
\[
S^{(l)}=S^{(l+1)}W^{(l+1)^T}F^{'(l)}(net^{(l)})\\
S^{(L)}=(Y-\hat{Y})F^{'(L)}(net^{(L)})
\]

\[
\frac{\partial E}{\partial W^{(l)}}=\left[\begin{matrix}h^{(l-1)}_1\\h^{(l-1)}_2 \\\dots \\h^{(l-1)}_{sl}\end{matrix}\right]S^{(l+1)}
\left[\begin{matrix}W_{11}^{(l+1)}&W_{12}^{(l+1)} &\dots& W_{2(sl+1)}^{(l+1)}\\
W_{21}^{(l+1)}&W_{22}^{(l+1)} &\dots& W_{2(sl+1)}^{(l+1)}\\
\dots&\dots&\dots&\dots\\
W_{sl1}^{(l+1)}&W_{sl2}^{(l+1)} &\dots& W_{sl(sl+1)}^{(l+1)}\\
\end{matrix} \right]^T\left[\begin{matrix} \partial f^{'(l)}(net_1^{l})&0&\dots & 0\\
0\\0 &\partial f^{'(l)}(net_2^{l})&\dots&0\\
0 & 0&\dots&0\\
0&0&\dots&\partial f^{'(l)}(net_l^{l})\end{matrix}\right]
\]

3.2 BP算法的小结

算法分为两个阶段：前向阶段和后向传播阶段

后向阶段算法：

Step 1: 计算\(\hat{y}^{(L)}\)

Step 2: for l =L:2

​ 计算\(S^{(l)}=S^{(l+1)}W^{(l+1)}F'(net^{(l)})\)

​ 计算 $\Delta W^{(l)}=h^{(l-1)}S^{(l)} $

​ 计算\(W^{(l)}=W^{(l)}-\delta \Delta W^{(l)}\)

3.3 Python实现

3.3.1 最简单三层网络

'''
不用任何框架，自己写一个三层的神经网络
# input-3,hidden-4 output-1
'''
import numpy as np

np.random.seed(1)

# Input Matrix
X = np.array([[0, 0, 1],
              [0, 1, 1],
              [1, 0 ,1],
              [1, 1, 1],])

# Output Matrix
y = np.array([[0],
              [1],
              [1],
              [0]])
# Nonlinear function
def sigmoid(X,derive=False):
    if not derive:
        return 1 / (1 + np.exp(-X))
    else:
        return X*(1-X)
# relu
def relu(X,derive = False):
    if not derive:
        return np.maximum(0,X)
    else:
        return (X>0).astype(float)

# Weight bias
W1 = 2 * np.random.random((3, 4))-1
b1 = 0.1 * np.ones((4,))

W2 = 2 * np.random.random((4,1))-1
b2 = 0.1 * np.ones((1,))

rate = 0.1
noline = relu
# Training
train_times = 200

for time in range(train_times):
    # Layer one
    A1 = np.dot(X,W1)+b1
    Z1 = noline(A1)
    # Layer two
    A2 = np.dot(Z1, W2)+b2
    Z2 = noline(A2)

    cost = -y+Z2

    # Calc deltas
    S2= cost*noline(A2,True)
    delta_W2 = np.dot(Z1.T,S2)
    bias2 = S2.sum(axis=0)

    S1 = np.dot(S2, W2.T)*noline(A1,True)
    delta_W1= np.dot(X.T, S1)
    bias1 = S1.sum(axis=0)
    # update
    W1 = W1-rate*delta_W1
    b1 = b1-rate*bias1
    W2 = W2-rate*delta_W2
    b2 = b2-rate*bias2

    print('error',np.mean(((y-Z2)*(y-Z2))**2))

print("prediction",Z2)

3.4 附录：

Name	Abbreviation
Mean absolute percentage error	MAPE
Root mean squares percentage error	RMSPE
Mean absolute percentage error	MAE
Mean squares error	MSE
Index of agreement	IA
Theil U statistic 1	U1
Theil U statistic 2	U2
Correlation coefficient	R

MAPE = \(\frac{1}{n} \sum_{k=1}^{n}\left|\frac{x^{(0)}(k)-\hat{x}^{(0)}(k)}{x^{(0)}(k)}\right| \times 100\)
RMSPE = \(\sqrt{\frac{1}{n} \sum_{k=1}^{n}\left(\frac{\hat{x}^{(0)}(k)-x^{(0)}(k)}{x^{(0)}(k)}\right)^{2}} \times 100\)
MAE = \(\frac{1}{n} \sum_{k=1}^{n}\left|\hat{x}^{(0)}(k)-x^{(0)}(k)\right|\)
MSE = \(\frac{1}{n} \sum_{k=1}^{n}\left(\hat{x}^{(0)}(k)-x^{(0)}(k)\right)^{2}\)
IA = \(1-\frac{\sum_{k=1}^{n}\left(\hat{x}^{(0)}(k)-x^{(0)}(k)\right)^{2}}{\sum_{k=1}^{n} \left( \left| \hat{x}^{(0)}(k)-\overline{x} \right|+\left| x^{(0)}(k)-\overline{x}\right| \right)^{2}}\)
U1 = \(\frac{\sqrt{\frac{1}{n} \sum_{k=1}^{n}\left(x^{(0)}(k)-x^{(0)}(k)\right)^{2}}}{\sqrt{\frac{1}{n} \sum_{k=1}^{n} x^{(0)}(k)^{2}}+\sqrt{\frac{1}{n} \sum_{k=1}^{n} x^{(0)}(k)^{2}}}\)
U2 = \(\frac{\left[\sum_{k=1}^{n}\left(\hat{x}^{(0)}(k)-x^{(0)}(k)\right)^{2}\right]^{1 / 2}}{\left[\sum_{k=1}^{n} x^{(0)}(k)^{2}\right]^{1 / 2}}\)
R = \(\frac{\operatorname{Cov}(\hat{x}^{(0)}, x^{(0)})}{\sqrt{\operatorname{Var}[\hat{x}^{(0)}] \operatorname{Var}[x^{(0)}]}}\)