C++版 - 剑指offer 面试题24：二叉搜索树BST的后序遍历序列(的判断) 题解

剑指offer 面试题24：二叉搜索树的后序遍历序列(的判断)

题目：输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则返回true。否则返回false。假设输入的数组的任意两个数字都互不相同。

提交网址： http://www.nowcoder.com/practice/a861533d45854474ac791d90e447bafd?tpId=13&tqId=11176

二叉搜索树(英语：Binary Search Tree)，也称二叉查找树、有序二叉树(英语：ordered binary tree)，排序二叉树（英语：sorted binary tree），是指一棵空树或者具有下列性质的二叉树：

1. 任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树；
4. 没有键值相等的节点。

         图1：3层二叉搜索树

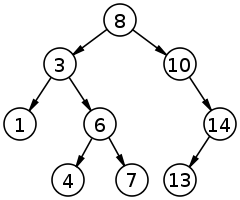
二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为O(log n)。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。

二叉查找树的查找过程和次优二叉树类似，通常采取二叉链表作为二叉查找树的存储结构。中序遍历二叉查找树可得到一个关键字的有序序列，一个无序序列可以通过构造一棵二叉查找树变成一个有序序列，构造树的过程即为对无序序列进行查找的过程。每次插入的新的结点都是二叉查找树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索、插入、删除的复杂度等于树高，期望O(log n)，最坏O(n)（数列有序，树退化成线性表）。

虽然二叉查找树的最坏效率是O(n),但它支持动态查询，且有很多改进版的二叉查找树可以使树高为O(log n), 如SBT、AVL树、红黑树。故不失为一种好的动态查找方法。

对于二叉搜索树BST，在树中任取一棵子树，其节点值都满足：左结点的值 < 父节点的值 < 右结点的值，故如果按照中序遍历的顺序遍历一棵二叉搜索树BST，遍历序列的数值是递增排序的。只需要用中序遍历算法遍历一棵二叉搜索树BST，就可以找出它的第k大结点。

1. 递归解法

由题意，可以将输入序列划分为3部分，即left、right、root，首先找到left部分最后一个结点的下标，即可完成分隔。如果left部分和right部分均是BST，即可递归调用VerifySquenceOfBST( )函数，变量bleft记录left部分是否为BST，bright记录right部分是否为BST。i从0~len-1对所有结点遍历一次... 最后的bleft&&bright即为所求的值。

6
      /      \
    3         8
  /   \      /   \
2     5    7    9

AC代码：

#include<cstdio>
#include<vector>
using namespace std;
class Solution{
public:
    bool VerifySquenceOfBST(vector<int> sequence)
	{
	int len=sequence.size();
	if(len<=0) return false;
	vector<int> left, right;
	int root=sequence[len-1];
	int i=0;
	while(i<len-1)  // 处理left部分
	{
		if(sequence[i]>root) break;
		left.push_back(sequence[i]);
		i++;
	}
	int j=i; // 处理right部分，此时i为left部分最后一个结点的下标
	while(j<len-1)
	{
		if(sequence[j]<root) return false;
		right.push_back(sequence[j]);
		j++;
	}
	bool bleft=true; // 应初始化为true，left部分是BST序列，才能调用VerifySquenceOfBST()
		if(i != 0) bleft=VerifySquenceOfBST(left); // i为left部分最后一个结点的下标 ，i!=0表示有左子树
	bool bright=true;
		if(i != len-1) bright=VerifySquenceOfBST(right);  // i!= len-1表示有右子树
	    return (bleft && bright);
    }
};
// 以下为测试部分
int main()
{
	Solution sol;
	vector<int> vec1={2,5,3,7,9,8,6};
	vector<int> vec2={5,7,6,9,11,10,8};
	vector<int> vec3={7,4,6,5};
	bool res1=sol.VerifySquenceOfBST(vec1);
	bool res2=sol.VerifySquenceOfBST(vec2);
	bool res3=sol.VerifySquenceOfBST(vec3);

	printf("%d\n",res1);
	printf("%d\n",res2);
	printf("%d\n",res3);
	return 0;
}

2. 非递归解法
左子树一定比右子树小，因此去掉根结点后，数字分为left，right两部分，right部分的最后一个数字是右子树的根，且它比左子树所有结点的值大，因此我们可以每次只看有子树是否符合条件即可，即使到达了左子树，左子树也可以看出由左右子树组成的树还像右子树那样处理.
对于左子树回到了原问题，对于右子树，左子树的所有值都比右子树的根小，可以暂时把他看出右子树的左子树，只需看看右子树的右子树是否符合要求即可.

例A：

6
      /      \
    3         8
  /   \      /   \
2     5    7    9

2 5 3 7 9 8 6
f -------------b
f -----------b
f --------b
f ------b

AC代码：

#include<cstdio>
#include<vector>
using namespace std;
class Solution
{
public:
    bool VerifySquenceOfBST(vector<int> sequence)
	{
        int backIdx = sequence.size();
        if(backIdx==0) return false;

        int forIdx = 0;
        while(--backIdx)  // backIdx=1时退出循环
        {
            while(sequence[forIdx]<sequence[backIdx])  forIdx++;     // forIdx从前往后扫描left部分
            while(sequence[forIdx]>sequence[backIdx])  forIdx++;     // forIdx从前往后继续扫描，主要扫right部分

            if(forIdx<backIdx) return false;    // 如果原序列是二叉搜索树BST的后序遍历序列，则终止时forIdx=backIdx
            forIdx=0;                           // 将forIdx拉回序列起点继续扫
        }
        return true;
    }
};

// 以下为测试部分
int main()
{
	Solution sol;
	vector<int> vec1={2,5,3,7,9,8,6};
	vector<int> vec2={5,7,6,9,11,10,8};
	vector<int> vec3={7,4,6,5};
	bool res1=sol.VerifySquenceOfBST(vec1);
	bool res2=sol.VerifySquenceOfBST(vec2);
	bool res3=sol.VerifySquenceOfBST(vec3);

	printf("%d\n",res1);
	printf("%d\n",res2);
	printf("%d\n",res3);
	return 0;
}

将此代码结合例A思考，还是不难理解的...