用turtle库实现汉诺塔问题~~~~~

汉诺塔问题

问题描述和背景：

汉诺塔是学习"递归"的经典入门案例，该案例来源于真实故事。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬在世界某个地方有个很虔诚的宗教组织，其中僧侣维护者一项神圣任务：保持宇宙的时间（好伟大啊....）。在时间的最开始（那时候有僧侣吗？），僧侣在平台上竖立了三个垂直杆，在最左侧杆上有64个不同半径金色同心圆盘，直径较大的圆盘堆放在下方，形成了金字塔形状的外观，僧侣们的任务是将所有圆盘从最左侧杆子移动到最右侧杆子上，这个宗教认为当僧侣们完成任务时，万事万物将会化为乌有，宇宙将结束（僧侣们内心该是怎样的~~(>_<)~~）。为了保持神圣的顺序，僧侣们移动圆盘需要遵从特定的规则：一次只能移动一个盘子、盘子只能在3个标杆之间移动、更大的盘子不能放在更小的盘子上面。

上星期的作业中我已经打出了输出步骤的Python代码，用了递归的思想，解决起来就很方便。先看看递归思想的解决方案吧。

代码如下：

def  move(n,a,b,c):
　　if n==:
　　　　print(a,'-->',c)
　　else:
　　　　move(n-,a,c,b)
　　　　move(,a,b,c)
　　　　move(n-,b,a,c)
move(,'A','B','C')

结果如图所示：

只要几行代码，就可以实现，但是要把这些可视化，又要怎么办呢？

今天就来尝试一下用Python强大的turtle库把汉诺塔问题可视化

emmmm我的能力有限，所以参考了网上的做法，代码如下：

一、设计一个类（Class）

类(Class):用来描述具有相同的属性和方法的对象的集合。它定义了该集合中每个对象所共有的属性和方法。对象是类的实例。

下面是此程序需用到的类（Class）代码：

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

二、设计汉诺塔的底座

为了还原汉诺塔的移动过程，增强可视化程度，我们给它加上三个底座，代码如下：

def drawpole_3():#画出汉诺塔的三个底座
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
　　　　 t.pencolor('blue')
        t.speed(100)
        t.goto(400*(k-1), 100)
        t.down()
        t.goto(400*(k-1), -100)
        t.goto(400*(k-1)-20, -100)
        t.goto(400*(k-1)+20, -100)
    drawpole_1(0)
    drawpole_1(1)
    drawpole_1(2)

三、制造汉诺塔的盘子

汉诺塔当然少不了盘子了，我们要写一段代码来绘制若干个盘子，代码如下：

def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,8-i)
        plates[i].goto(-400,-90+20*i)
        plates[i].showturtle()
    return plates

四、制造一个底座的栈

栈：栈作为一种数据结构，是一种只能在一端进行插入和删除操作。它按照先进后出的原则存储数据，先进入的数据被压入栈底，最后的数据在栈顶，需要读数据的时候从栈顶开始弹出数据（最后一个数据被第一个读出来）。昨天刚刚好学了栈，现在正好拿来试试手（嘿嘿嘿）

此处使用的栈并非Python中真正意义上的栈，而是与之意思相仿的说法，我们都知道，汉诺塔必须将最上的盘子取走方可移动第二层的盘子，以此类推，不移动上方的盘子，就无法移动下方的盘子，废话不多说，来看看这个代码吧：

def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles

五、设计移动盘子的代码

准备完前面的工作，现在就要开始移动盘子了，代码如下：

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*400,150)
    plates[mov].goto((tp-1)*400,150)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*400,-90+20*l)

六、设计操控盘子移动方向的代码

可以移动盘子了当然还不够，只是胡乱地移动无法解决汉诺塔问题，我们要让盘子向着能够解决问题的方向移动，代码如下：

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)

七、调用

终于完成了全部准备工作，现在就来调用函数，让他们一起发挥作用吧！

import turtle

class Stack:
    def __init__(self):
        self.items = []
    def isEmpty(self):
        return len(self.items) == 0
    def push(self, item):
        self.items.append(item)
    def pop(self):
        return self.items.pop()
    def peek(self):
        if not self.isEmpty():
            return self.items[len(self.items) - 1]
    def size(self):
        return len(self.items)

def drawpole_3():#画出汉诺塔的poles
    t = turtle.Turtle()
    t.hideturtle()
    def drawpole_1(k):
        t.up()
        t.pensize(10)
        t.speed(100)
        t.goto(400*(k-1), 100)
        t.down()
        t.goto(400*(k-1), -100)
        t.goto(400*(k-1)-20, -100)
        t.goto(400*(k-1)+20, -100)
    drawpole_1(0)#画出汉诺塔的poles[0]
    drawpole_1(1)#画出汉诺塔的poles[1]
    drawpole_1(2)#画出汉诺塔的poles[2]

def creat_plates(n):#制造n个盘子
    plates=[turtle.Turtle() for i in range(n)]
    for i in range(n):
        plates[i].up()
        plates[i].hideturtle()
        plates[i].shape("square")
        plates[i].shapesize(1,8-i)
        plates[i].goto(-400,-90+20*i)
        plates[i].showturtle()
    return plates

def pole_stack():#制造poles的栈
    poles=[Stack() for i in range(3)]
    return poles

def moveDisk(plates,poles,fp,tp):#把poles[fp]顶端的盘子plates[mov]从poles[fp]移到poles[tp]
    mov=poles[fp].peek()
    plates[mov].goto((fp-1)*400,150)
    plates[mov].goto((tp-1)*400,150)
    l=poles[tp].size()#确定移动到底部的高度（恰好放在原来最上面的盘子上面）
    plates[mov].goto((tp-1)*400,-90+20*l)

def moveTower(plates,poles,height,fromPole, toPole, withPole):#递归放盘子
    if height >= 1:
        moveTower(plates,poles,height-1,fromPole,withPole,toPole)
        moveDisk(plates,poles,fromPole,toPole)
        poles[toPole].push(poles[fromPole].pop())
        moveTower(plates,poles,height-1,withPole,toPole,fromPole)

myscreen=turtle.Screen()
drawpole_3()
n=int(input("请输入汉诺塔的层数并回车:\n"))
plates=creat_plates(n)
poles=pole_stack()
for i in range(n):
    poles[0].push(i)
moveTower(plates,poles,n,0,2,1)
myscreen.exitonclick()

八、效果

首先输入一下我们想测试的汉诺塔层数，为节省时间我就选择了3层（之前C语言的课上老师演示了一遍20个盘子的输出步骤，结果运行了一节课，Python的运行比较慢，三个盘子就够了~~~~）

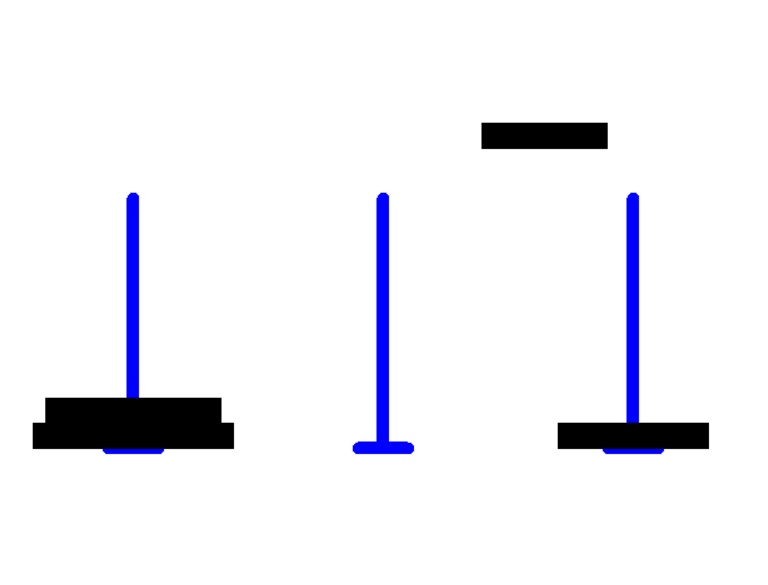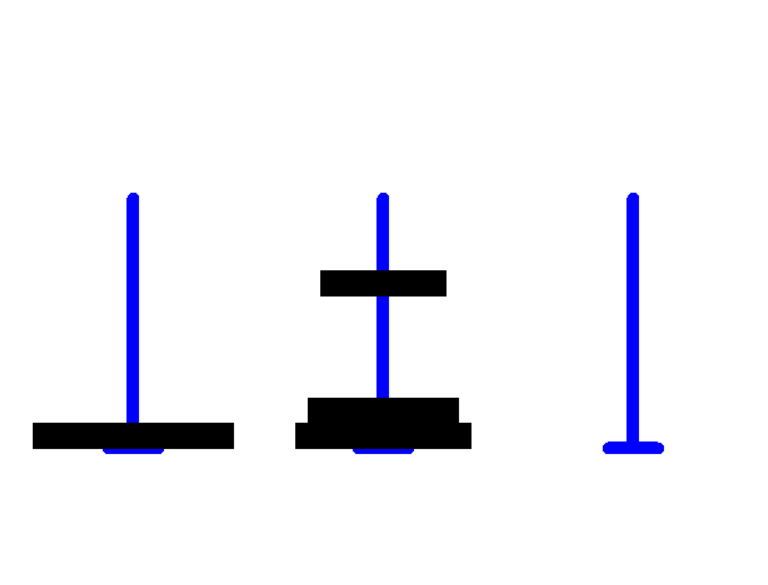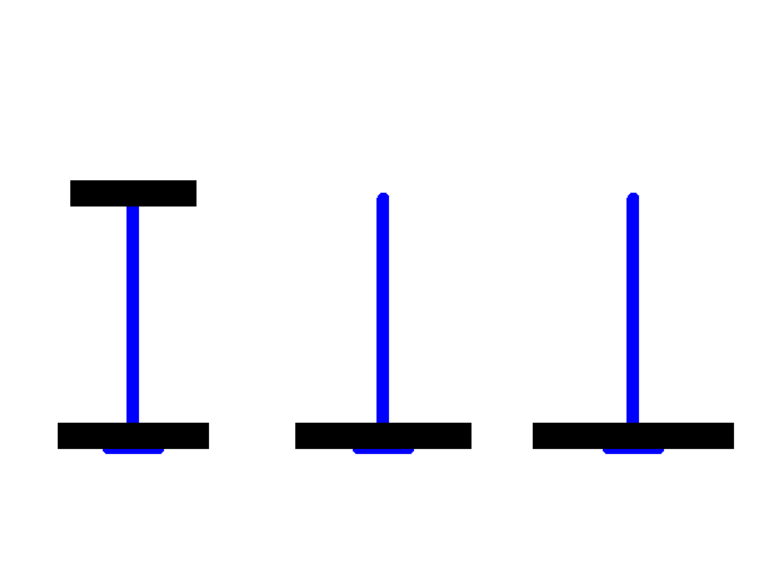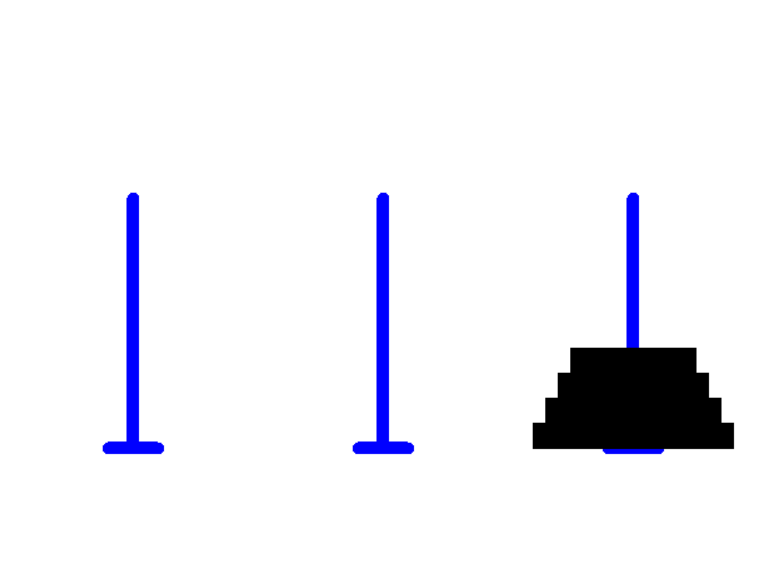
这样就实现了，通过封装多个不同功能的python代码，结合多个方法就可以实现这样看似复杂的实现！

【累死了，敲这么长的代码真是个体力活。】