luogu 1268 树的重量

打眼一看就是最小生成树嘛，但经过板子wa掉的经历后得知,,emmmm,原来是,

构造！

(虽然不知是什么但觉得听起来很厉害的样子...手动微笑)

n=2的情况 自然就是g(1,2)

n=3的情况，由于所有点均为叶子节点，运用树的性质，蓝线部分的 len=(g(1,3)+g(2,3)-g(1,2)) / 2

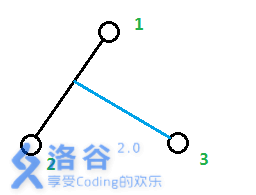
n>3的情况也同理，枚举i看点n是不是从1~i的路径上分叉出来的，求出最小的len加入答案即可

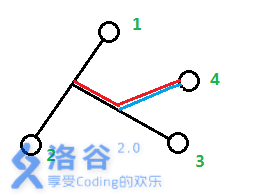
若认为点4是从1~2的路径上分叉出来的，答案就会加上红色部分长度。但是红色部分长度有一部分多余，只有点4是从1~3路径上分叉出来的，才能加上正确答案(蓝色部分)

(洛谷的水印似乎暴露了些什么，消不掉我也很无奈....)

构造好题

#pragma GCC optimize(3)
#include<bits/stdc++.h>
using namespace std;
const int maxn=;
const int INF=(<<);
int d[maxn][maxn];
int main()
{
    int n;
    while(scanf("%d",&n)==&&n)
    {
        for(int i=;i<=n;i++)
        for(int j=i+;j<=n;j++)
            scanf("%d",&d[i][j]),d[j][i]=d[i][j];
        int ans=d[][];
        for(int i=;i<=n;i++){
            int t=INF;
            for(int j=;j<i;j++)
               t=min(t,(d[][i]+d[j][i]-d[][j])/);
            ans+=t;
        }
        printf("%d\n",ans);
    }
    return ;
}

以上