每月学习数理统计--《统计学习方法

1. SVM的最优化问题

　　支持向量机（Support Vector Machine, SVM）的基本模型是在特征空间上找到最佳的分离超平面使得训练集上正负样本间隔最大。SVM是用来解决二分类问题的有监督学习算法，在引入了核方法之后SVM也可以用来解决非线性问题。
一般SVM有下面三种：

　　硬间隔支持向量机（线性可分支持向量机）：当训练数据线性可分时，可通过硬间隔最大化学得一个线性可分支持向量机。
软间隔支持向量机：当训练数据近似线性可分时，可通过软间隔最大化学得一个线性支持向量机。
非线性支持向量机：当训练数据线性不可分时，可通过核方法以及软间隔最大化学得一个非线性支持向量机

　　在SVM中，我需要的是找到一个超平面，定义几何间隔M定义为：

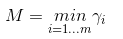
其中

那么我们要做的就是找到最大间隔，又因为

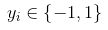
所以在最大间隔中，即

所以我们的问题就变成

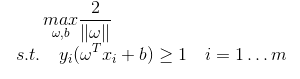
即

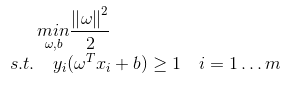
　　为什么我们要费这么⼤的劲去重写这个问题？因为原始的最优化问题很难解，作为替代，我们现在有凸⼆次函数最优化问题，虽然它平淡⽆奇，但是⾮常容易解。

2. 凸优化问题的解法

1. 拉格朗日乘数法

我们求最优解问题：

即我们找最小值就是在同一个方向的梯度点符合条件，也就是求出

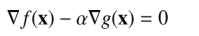
通常我们称a为拉格朗日乘子。

拉格朗⽇乘数法能总结为以下三步：

1．通过每⼀个带乘⼦的约束条件来构造拉格朗⽇函数
2．给出拉格朗⽇函数的梯度
3．解函L(x, a)=0

所以通过我们列出的条件便可以写出拉格朗日函数

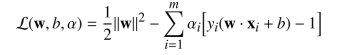
2. 对偶问题

我们在列出拉格朗日函数后，我们发现优化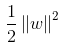就是优化我们的拉格朗日函数，约束条件就是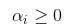,所以我们的目标函数可以表示为

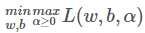
也就是

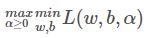
所以我们先求w和b的最小值，求这个最小值演化为L的偏导数中求w和b：

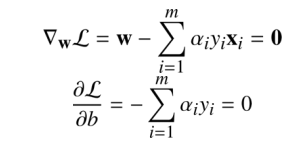
因此我们发现

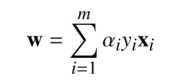
同时考虑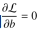那么我们可以写出我们的式子

所以我们的问题演化为一个对偶问题

上式可知我们并不关心单个样本是如何的，我们只关心样本间两两的乘积，这也为后面核方法提供了很大的便利。
求解出α之后，再求解出w和b即可得到SVM决策模型。

实际上，我在学习其他书本后发现了一个很重要的地方，就是这个$\alpha $实际上是点与点的权重，那么这里面就隐藏着一个很重要的东西，就是：离SVM vector越远的点，他的权重就越小，虽然这句话很直观，而且很朴实，但是实际上这里面蕴藏着很多的调试方法与对SVM的理解。希望大家在使用SVM的时候要记住这一点。

3. KKT条件(Karush-Kuhn-Tucker)

所谓KKT条件，就是如果一个解法满足KKT条件，那么这个解法就是一个最优解法（是不是特别神奇！）那么这个KKT条件必须满足以下四条：

稳定条件（L函数在w的梯度为0，在b处的梯度也为0）

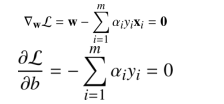
原可行条件

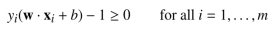
对偶可行条件

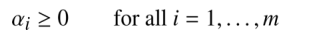
互补松弛条件

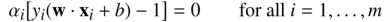
　　如果αi=0则由式(15)可知该样本点对求解最佳超平面没有任何影响。当αi>0时必有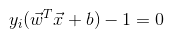，表明对应的样本点在最大间隔边界上，即对应着支持向量。也由此得出了SVM的一个重要性质：训练完成之后，大部分的训练样本都不需要保留，最终的模型仅与支持向量有关[2]。从另一个角度，如果SVM的超平面主要与支持向量有关，同时大多数的均为0。

　　同时，我们知道了，最终问题我们便是求解，只要我们将求解出来，那么我们的w与b也就求解出来了。这里有两种方法求解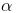，QP法与SMO方法。

3. 软间隔支持向量机

　　这里有一个很严重的问题，我们之前讲的问题，就必须要求数据集是可分的，而实际上，数据经常会出现又异常情况出现，通常来说，这些数据异常通常接近分类边界，如下图所示，只有一个数据异常，却破坏了线性可分。

对于这种情况，我们使用软边界，目的不是做到0错误，而是允许少量的错误

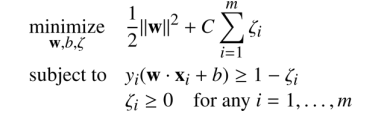
参数C让我们控制如何让SVM来处理错误。让我们举例说明如何去改变它的值来得到不同的超平⾯

4. 非线性支持向量机

　　我们知道，有很多情况下，许多数据集都是不可分的，他们的分布是非常复杂，我们可以在直接处理这些数据集之前，对数据集做一些变换，目的是为了将数据集分布改变，一个合适的变化，可以将一个数据集变得非常简单可分，同时满足需求。我们知道，在对偶问题中，

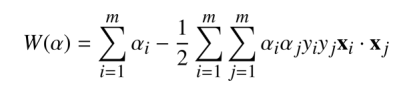
点积实际上可以用其他算法替代，本质上来说，我们是重新定义内积，因为内积只要满足正定，双线性那三个性质即可，那么我们在求解内积的时候，便可以对数据集实现变换，让其变得可分。一般来说，我们使用的是标准内积。

　　通常来说，我们使用不同的核，就是使用不同的内积，包括高斯核，RBF核，多项式核，线性核，他们无非是实现了广度，深度的增加，或者是是对原数据集做线性变换。本质上还是不同的内积，所以非线性支持向量机是非常简单的。

5. SMO算法

通常来说，我们有很多成熟的软件包来实现SVM，但是那样的解法是没有灵魂了。当然了，这个部分我也没有理解的太深刻，所以并不敢写出来，所以我只能分享一个博主写的有关SMO的算法的文章，希望大家能多看看，等我完全搞懂了以后我便会重新写出来。这一篇我认为是写的最为详细的文章了：https://blog.csdn.net/jesmine_gu/article/details/84024702