树形dp 入门
今天学了树形dp，发现树形dp就是入门难一些，于是好心的我便立志要发一篇树形dp入门的博客了。
树形dp的概念什么的，相信大家都已经明白，这里就不再多说。直接上例题。
一、常规树形DP
题目描述
某大学有N个职员，编号为1~N。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数Ri，但是呢，如果某个职员的上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。
这是一道非常经典的树形dp，首先分析题目，如果上司去了，那么他的所有下司都不能去；如果上司不去，那么他的所有下司去不去无所谓，但要取最大值。接下来就是状态转移方程：
我们设f[i][0]为i不去的情况，f[i][1]为i去的情况，那么
f[i][0]+=max(f[i的下司][1],f[i的下司][0]);
f[i][1]+=f[i的下司]][0];
初始化，如果i去，那么显然f[i][1]=i的快乐指数，如果i不去那么f[i][1]=0；
最后贴上代码
#include<iostream>
#include<cstring>
#include<cmath>
#include<string>
#include<cstdio>
using namespace std;
struct edge
{
int num,child[];
}g[];
int n;
int a[];
int tree[];
int f[][];
int aa,bb,root;
void dp(int t)
{
f[t][]=a[t];//初始化
f[t][]=;//初始化
for(int i=;i<=g[t].num;i++)
{
dp(g[t].child[i]);
f[t][]+=max(f[g[t].child[i]][],f[g[t].child[i]][]);//状态转移
f[t][]+=f[g[t].child[i]][];//状态转移
}
}
int main()
{
cin>>n;
for(int i=;i<=n;i++)
{
scanf("%d",&a[i]);
}
while(scanf("%d%d",&aa,&bb))
{
if(aa==&&bb==) break;
g[bb].num++;//记录孩子结点的个数
g[bb].child[g[bb].num]=aa;//储存孩子结点
tree[aa]=bb;//记录父亲结点
}
root=;
while(tree[root]) root++;//找出树根
dp(root);//从树根开始dp
int ans=max(f[root][],f[root][]);
cout<<ans;
return ;
}
题目描述
Bob喜欢玩电脑游戏，特别是战略游戏。但是他经常无法找到快速玩过游戏的办法。现在他有个问题。
他要建立一个古城堡，城堡中的路形成一棵树。他要在这棵树的结点上放置最少数目的士兵，使得这些士兵能了望到所有的路。
注意，某个士兵在一个结点上时，与该结点相连的所有边将都可以被了望到。
请你编一程序，给定一树，帮Bob计算出他需要放置最少的士兵.
和上个题一模一样，就是初始化不同，上个题每个人都有不同的权值，而这个题每个人的权值都为1；
状态转移一模一样 ；初始化，f[i][1]=1，f[i][1]=0；
最后上代码
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int num,child[];
}g[];
int a[];
int f[][];
int x,y;
int n;
void dp(int t)
{
f[t][]=;//初始化为1
f[t][]=;
for(int i=;i<=g[t].num;i++)
{
dp(g[t].child[i]);
f[t][]+=f[g[t].child[i]][];//状态转移
f[t][]+=min(f[g[t].child[i]][],f[g[t].child[i]][]);//状态转移
}
}
int main()
{
cin>>n;
for(int i=;i<=n;i++)
{
scanf("%d",&x);
scanf("%d",&g[x].num);//记录该结点的孩子个数
for(int j=;j<=g[x].num;j++)
{
scanf("%d",&g[x].child[j]);//存储该结点的孩子
a[j]=i;//记录父亲
}
}
int root=;
while(a[root]) root++;//找出根节点
dp(root);
int ans=min(f[root][],f[root][]);
cout<<ans;
return ;
}
洛谷P2458 [SDOI2006]保安站岗
题目描述
五一来临，某地下超市为了便于疏通和指挥密集的人员和车辆，以免造成超市内的混乱和拥挤，准备临时从外单位调用部分保安来维持交通秩序。
已知整个地下超市的所有通道呈一棵树的形状；某些通道之间可以互相望见。总经理要求所有通道的每个端点（树的顶点）都要有人全天候看守，在不同的通道端点安排保安所需的费用不同。
一个保安一旦站在某个通道的其中一个端点，那么他除了能看守住他所站的那个端点，也能看到这个通道的另一个端点，所以一个保安可能同时能看守住多个端点（树的结点），因此没有必要在每个通道的端点都安排保安。
编程任务：
请你帮助超市经理策划安排，在能看守全部通道端点的前提下，使得花费的经费最少。
难度提升，如果看不懂可以先放一放
分析：
我们发现，要使所有点最终全部被覆盖，那么无非有3种状态：
（以下全部都是对于要覆盖任意一个以x为根的子树来说的）
（其中我们设y节点为y的儿子，fa为x的父亲）
1.x节点被自己覆盖，即选择x点来覆盖x点
2.x节点被儿子y覆盖，即选择y点来覆盖x点
3.x节点被父亲fa覆盖，即选择fa点来覆盖x点借此三种状态，我们可以设f[x][0/1/2]为让以x为根的子树中的节点全部被覆盖，且x点的被覆盖情况为1/2/3时的最小代价
为了方便，我们不妨设这三种情况分别为：
1.f[x][0]---对应上面的1
2.f[x][1]---对应上面的2
3.f[x][2]---对应上面的3
既然是DP，总是有转移方程的，我们想一下dp方程要如何设计
设计状态转移方程：
(1):对应上面的1.
f[x][0]=∑ min(f[y][0],f[y][1],f[y][2]) + val[x]
其中val[x]是选择x点的代价
我们很容易想到，在节点x被选择之后，我们就可以无拘无束了（蛤?），也就是说对于x儿子节点y的状态可以不去考虑，因为x节点被选择之后y节点无论如何也会被覆盖到，所以我们在儿子y的所有状态里取min，累加起来就行了
(2):对应上面的3（先讲3，因为2比较难以理解，放到了后面）
f[x][2]=∑ min(f[y][0],f[y][1])
为什么3情况对应的转移方程要这样写呢?
我们不妨这样理解，对于x节点我们让它的父亲节点fa覆盖它，那么根据我们的状态设计，此时必须要满足以x的儿子y为根的子树之中所有点已经被覆盖
那么这时就转化为一个子问题，要让y子树满足条件，只有两种决策：要么y被y的儿子覆盖，要么被y自己覆盖（即选择y节点），只需要在y的这两种状态取min累加就可以了
(3):对应上面的2（DuangDuangDuang 敲黑板划重点啦）
f[x][1]=∑ min(f[y][0],f[y][1])，如果选择的全部都是f[y][1],要再加上min(f[y][0]-f[y][1])
到了这里，我们就要回顾一下我们设计的dp状态了：
设f[x][0/1/2]为让以x为根的子树中的节点全部被覆盖，且x点的被覆盖情况为1/2/3时的最小代价
先提示一下，如果你理解了下面，那么本题是很简单的。。如果你没理解，就返回到这里再看一遍吧，我就在这里等着你
对于此时的状态，f[x][1]代表对于节点x让x被自己的儿子覆盖，那么和分析（2）一样，都要先满足此时以y的子树已经满足了条件，才能进行转移，这就是前面那部分：∑ min(f[y][0],f[y][1])的来历，那么后面那一长串又是怎么回事呢?
我们可以这样理解，此时既然要保证x点是被自己的儿子覆盖的，那么如果此时y子树已经满足了全部被覆盖，但是y此时被覆盖的状态却是通过y节点自己的儿子达到的，那么x就没有被儿子y覆盖到，那么我们不妨推广一下，如果x所有的儿子y所做的决策都不是通过选择y点来满足条件，那么我们就必须要选择x的一个子节点y，其中y满足f[y][0]-f[y][1]最小，并把这个最小的差值累加到f[x][1]中去，这样才能使得x点被自己的儿子覆盖，状态f[x][1]也才能合理地得到转移
好了，如果你还是没有太懂这个（3）的设计过程，请你回到之前再仔细看几遍
如果你已经理解了上面，那么恭喜你这个题，你已经A掉了
因为转移方程既然有了，那么我们就只需要最后的答案了
由于题目中没有说这棵树的根节点是哪个，所以你可以默认1就是根，或者开一个数组在加边的时候记录一下每个点的入度，最后没有入度的点就是根（但好像没有区别，毕竟我A掉了）
最后答案即为min(f[root][0],f[root][1])
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int num,child[];
}g[];
int a[];
int dp[][];
int root[];
int n,aa;
void dfs(int x)
{
dp[x][]=a[x];
int cc=;
int num=;
for(int i=;i<=g[x].num;i++)
{
dfs(g[x].child[i]);
int t=min(dp[g[x].child[i]][],dp[g[x].child[i]][]);
dp[x][]+=min(t,dp[g[x].child[i]][]);
dp[x][]+=t;
dp[x][]+=t;
if(dp[g[x].child[i]][]<dp[g[x].child[i]][]) num++;
else cc=min(cc,dp[g[x].child[i]][]-dp[g[x].child[i]][]);
}
if(num==) dp[x][]+=cc;
}
int main()
{
scanf("%d",&n);
for(int i=;i<=n;i++)
{
scanf("%d",&aa);
scanf("%d",&a[aa]);
scanf("%d",&g[aa].num);
for(int j=;j<=g[aa].num;j++)
{
scanf("%d",&g[aa].child[j]);
root[g[aa].child[j]]=aa;
}
}
aa=;
while(root[aa]) aa++;
dfs(aa);
cout<<min(dp[aa][],dp[aa][]);
return ;
}
二、树形背包问题(在树上进行分组背包处理)
这类问题就是让你求在树上选规定数目的点满足价值最大的问题，一般都可以设f[i][j]表示i这棵子树选j个点的最优解。
洛谷P2015 二叉苹果树
题目描述
有一棵苹果树，如果树枝有分叉，一定是分2叉（就是说没有只有1个儿子的结点）
这棵树共有N个结点（叶子点或者树枝分叉点），编号为1-N,树根编号一定是1。
我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。下面是一颗有4个树枝的树
2 5
\ /
3 4
\ /
1现在这颗树枝条太多了，需要剪枝。但是一些树枝上长有苹果。
给定需要保留的树枝数量，求出最多能留住多少苹果。
很典型的一道树形dp题目。我们设dp[i][j]为在以i为根的子树上取j个点的最大值，因为苹果树是二叉树，所以如果在左子树上
取k个点，那么就在右子树上取j-k个点，状态转移方程为：
dp[i][j]=max(dp[i][j],dp[i][k]+dp[v][j-k]); 其中v表示i的子节点。
代码如下：
#include<iostream>
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int next;
int to;
int dis;
}g[];
int n,m;
int last[];
int dp[][];
int num;
int aa,bb,cc;
void dfs(int x,int fa)
{
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dp[v][]=g[i].dis;
dfs(v,x);
for(int j=m;j>=;j--)
for(int k=;k<=j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//状态转移
}
}
}
}
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int main()
{
scanf("%d%d",&n,&m);
m++;//由于题目给的是树枝的数量，所以结点数等于树枝树加1。
for(int i=;i<n;i++)
{
scanf("%d%d%d",&aa,&bb,&cc);
add(aa,bb,cc);
add(bb,aa,cc);
}
dfs(,);//从根节点开始搜索
cout<<dp[][m];
return ;
}
洛谷P2014 选课
题目描述
在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有N门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程a是课程b的先修课即只有学完了课程a，才能学习课程b）。一个学生要从这些课程里选择M门课程学习，问他能获得的最大学分是多少？
大体思路和上个题相同，只不过这道题的数据是一个森林结构，我们可以自己添加一个结点作为整个森林的
根节点，于是就把一个森林变成了一棵树，对于虚拟的根我们只需要将所选的结点数加上1即可。
其他的地方跟上个题完全一样，这里不再多说，直接上代码：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int next;
int to;
}g[];
int last[];
int aa;
int n,m;
int num;
int a[];
int dp[][];
void dfs(int x,int fa)
{
dp[x][]=a[x];//初始化为选x这门课程的学分
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(v,x);
for(int j=m;j>=;j--)
for(int k=;k<=j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//状态转移
}
}
}
}
void add(int from,int to)
{
g[++num].next=last[from];
g[num].to=to;
last[from]=num;
}
int main()
{
scanf("%d%d",&n,&m);
m++;//因为加了一个虚拟的根，所以要将结点数加上1，这里一定要注意！！！
for(int i=;i<=n;i++)
{
scanf("%d%d",&aa,&a[i]);//用a数组来表示选i这门课程的学分
add(aa,i);
add(i,aa);
}
dfs(,);//从虚拟的跟结点开始搜索
cout<<dp[][m];
return ;
}
和上一个题几乎一样，还是注意添加一个虚拟的根结点，添加后记得将总结点数加1.这道题是多组数据
所以记得清空数组，其他都一模一样。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
using namespace std;
struct edge
{
int next;
int to;
}g[];
int last[];
int a[];
int dp[][];
int aa;
int num;
int n,m;
void add(int from,int to)
{
g[++num].next=last[from];
g[num].to=to;
last[from]=num;
}
void dfs(int x,int fa)
{
dp[x][]=a[x];
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(v,x);
for(int j=m;j>=;j--)
for(int k=;k<=j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);
}
}
}
}
int main()
{
while()
{
scanf("%d%d",&n,&m);
if(n==&&m==) return ;
m++;//这里要加1.
num=;
memset(a,,sizeof(a));//千万记得清空数组！！！
memset(dp,,sizeof(dp));
memset(last,,sizeof(last));
memset(g,,sizeof(g));
for(int i=;i<=n;i++)
{
scanf("%d%d",&aa,&a[i]);
add(aa,i);
add(i,aa);
}
dfs(,);
printf("%d\n",dp[][m]);
}
}
杀死所有的bug总是比抓住他们的大脑更容易。为您绘制一张地图，所有房间都标有内部虫子的数量，以及包含大脑的可能性。洞穴的结构就像一棵树，从入口处有一条通往每个房间的独特路径。为了尽快完成战斗，你不想等到部队人员在前进到下一个房间之前清理房间，而是你必须在每个房间留下一些士兵来对抗里面的所有虫子。这些士兵从未重新进入他们之前访问过的房间。
星舰士兵可以对抗20个虫子。由于你没有足够的士兵，你只能占用一些房间，让神经气体完成其余的工作。同时，你应该最大限度地捕获大脑的可能性。为了简化问题，只需最大化所有可能的房间包含大脑的总和。制定这样的计划是一项艰巨的任务。你需要一台电脑的帮助。
最后一个测试用例后跟两个-1。
50 10
40 10
40 20
65 30
70 30
1 2
1 3
2 4
2 5
1 1
20 7
-1 -1
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
using namespace std;
struct edge
{
int next;
int to;
}g[];
int last[];
int a[];
int b[];
int dp[][];
int aa,bb;
int num;
int n,m;
void add(int from,int to)
{
g[++num].next=last[from];
g[num].to=to;
last[from]=num;
}
void dfs(int x,int fa)
{
for(int i=a[x];i<=m;i++)//这里的初始化和上面的题目不同，因为有点权。
dp[x][i]=b[x];//当我们有a[x]名队员以至于更多时,我们最少可以获得b[x]个大脑
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(v,x);
for(int j=m;j>=a[x];j--)//这里的边界条件应该注意一下
for(int k=a[x];k<j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]);//一样的状态转移方程
}
}
}
}
int main()
{
while()
{
scanf("%d%d",&n,&m);
if(n==-&&m==-) return ;
num=;
memset(a,,sizeof(a));
memset(b,,sizeof(b));
memset(dp,,sizeof(dp));
memset(last,,sizeof(last));
memset(g,,sizeof(g));//清空数组，基本操作
for(int i=;i<=n;i++)
{
scanf("%d%d",&aa,&bb);
aa=(aa+)/;
a[i]=aa;//读入点权
b[i]=bb;
}
for(int i=;i<n;i++)
{
scanf("%d%d",&aa,&bb);
add(aa,bb);
add(bb,aa);
}
if(m==)//这里很坑，如果m=0一定要输出0；
printf("0\n");
else //否则就开始搜索
{
dfs(,);
printf("%d\n",dp[][m]);
}
}
}
题目描述
某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构，这棵树的根结点位于足球比赛的现场，树叶为各个用户终端，其他中转站为该树的内部节点。
从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的，一场转播的总费用等于传输信号的费用总和。
现在每个用户都准备了一笔费用想观看这场精彩的足球比赛，有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。
写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
输入输出格式
输入格式：
输入文件的第一行包含两个用空格隔开的整数N和M，其中2≤N≤3000，1≤M≤N-1，N为整个有线电视网的结点总数，M为用户终端的数量。
第一个转播站即树的根结点编号为1，其他的转播站编号为2到N-M，用户终端编号为N-M+1到N。
接下来的N-M行每行表示—个转播站的数据，第i+1行表示第i个转播站的数据，其格式如下：
K A1 C1 A2 C2 … Ak Ck
K表示该转播站下接K个结点(转播站或用户)，每个结点对应一对整数A与C，A表示结点编号，C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。
输出格式：
输出文件仅一行，包含一个整数，表示上述问题所要求的最大用户数。
输入输出样例
5 3
2 2 2 5 3
2 3 2 4 3
3 4 2
2 有些难度的树上背包问题。首先应该明确，题目要求的用户数是叶子结点的数目，而不包括非叶子结点，所以我们在搜索的时候
可以顺便记录一下，在做背包的时候，只需要循环这个子树上的叶子结点数即可。
我们设dp[i][j]为在以i为根的子树上选取j个叶子结点所得到的最大收益。 而收益值等于点权减去边权，所以可以推出状态
转移方程：dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]-g[i].dis); 其中v代表x的子结点
然后我们在枚举以1为根的树上最多选取多少个叶结点可以是最大收益值非负。
由于收益可能是负的，所以要把数组清为负无穷。
最后上代码：
#include<iostream>
#include<cstdio>
#include<string>
#include<cmath>
#include<cstring>
using namespace std;
struct edge
{
int next;
int to;
int dis;
}g[];
int last[];
int a[];
int dp[][];
int aa,bb,cc;
int n,m,num;
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int dfs(int x,int fa)
{
if(x>=n-m+)//如果x为叶子节点，那么就初始化为这个点的点权
{
dp[x][]=a[x];
return ;//记录叶子节点个数
}
int t,sum=;
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
t=dfs(v,x);//t表示以v为根的树的叶子节点个数
sum+=t;//sum表示以x为根的树的叶子节点个数
for(int j=sum;j>=;j--)
for(int k=;k<=j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k]-g[i].dis);//状态转移
}
}
}
return sum;
}
int main()
{
scanf("%d%d",&n,&m);
memset(dp,~0x3f,sizeof(dp));//清为负无穷
for(int i=;i<=n-m;i++)
{
scanf("%d",&aa);
for(int j=;j<=aa;j++)
{
scanf("%d%d",&bb,&cc);//读入边权
add(i,bb,cc);
add(bb,i,cc);
}
}
for(int i=n-m+;i<=n;i++)
{
scanf("%d",&a[i]);//读入点权
}
for(int i=;i<=n;i++) dp[i][]=;//这里很重要，如果选0个子结点那么收益一定为0；
dfs(,);
for(int i=m;i>=;i--)
{
if(dp[][i]>=)//如果收益值非负，那么第一个i就是最大值。
{
cout<<i;
return ;
}
}
}
题目描述
经过数月的精心准备，Peer Brelstet，一个出了名的盗画者，准备开始他的下一个行动。艺术馆的结构，每条走廊要么分叉为两条走廊，要么通向一个展览室。Peer知道每个展室里藏画的数量，并且他精确测量了通过每条走廊的时间。由于经验老到，他拿下一幅画需要5秒的时间。你的任务是编一个程序，计算在警察赶来之前，他最多能偷到多少幅画。
输入输出格式
输入格式：
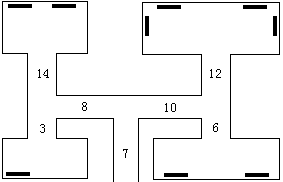
第1行是警察赶到的时间，以s为单位。第2行描述了艺术馆的结构，是一串非负整数，成对地出现：每一对的第一个数是走过一条走廊的时间，第2个数是它末端的藏画数量；如果第2个数是0，那么说明这条走廊分叉为两条另外的走廊。数据按照深度优先的次序给出，请看样例。
一个展室最多有20幅画。通过每个走廊的时间不超过20s。艺术馆最多有100个展室。警察赶到的时间在10min以内。
输出格式：
输出偷到的画的数量
输入输出样例
60
7 0 8 0 3 1 14 2 10 0 12 4 6 2
2 这题的读入比较毒瘤，需要递归来读，如果读到房间就把房间中的画存下来。其他都还好。
我们设dp[i][j]表示在以i为根的子树上用j的时间可以偷到的最多画的数目，
dp[i][j]=max(dp[i][j],dp[i][k]+dp[v][j-k-g[i].dis);其中v是i的子节点，
g[i].dis表示i到v的距离。由于偷完画后需要出来，所以就需要将边权乘以2计算，而且需要在警察来之前跑出来，因此总时间应减1。
代码如下：
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int next;
int to;
int dis;
}g[];
int last[];
int dp[][];
int num,aa,bb,cc;
int a=;
int s;
void add(int,int,int);
void dfs(int x)
{
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
dfs(v);
for(int j=s;j>=;j--)
for(int k=;k<=j;k++)
{
if(j-k-g[i].dis>=)
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k-g[i].dis]);//状态转移
} }
}
void read(int faa)
{
scanf("%d%d",&aa,&bb);
add(faa,a+,aa*);
a++;
if(bb==)
{
faa=a;
read(faa);
read(faa);
}
else
{
for(int i=;i<=bb;i++)
{
dp[a][i*]=i;
}
}
}
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int main()
{
scanf("%d",&s);
s--;//由于需要在警察来之前出来，所以总时间减1。
read();//毒瘤的读入
dfs();//从根节点开始搜索
cout<<dp[][s];
return ;
}
其实我们机房的某位大神还有一种独特的思路，他用f[i][j]表示以i为根的子树上偷j幅画所用的时间。
不得不说这是真的强。
附上代码：
#include<iostream>
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
using namespace std;
struct edge
{
int next;
int to;
int dis;
}g[];
int s;
int aa,bb;
int x=;
int last[];
int dp[][];
int tree[];
int num,faa;
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int dfs(int y,int fa)
{
if(tree[y]==)
{
dp[y][]=;
return ;
}
int t,sum=;
for(int i=last[y];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
t=dfs(v,y);
sum+=t;
for(int j=sum;j>=;j--)
for(int k=;k<j;k++)
{
dp[y][j]=max(dp[y][j],dp[y][k]+dp[v][j-k]-g[i].dis);
}
}
}
return sum;
}
void read(int faa)
{
scanf("%d%d",&aa,&bb);
add(faa,x+,*aa);
add(x+,faa,*aa);
x++;
if(bb==)
{
faa=x;
read(faa);
read(faa);
}
else
{
int fa=x;
for(int i=;i<=bb;i++)
{
tree[x+]=;
add(fa,x+,);
add(x+,fa,);
x++;
}
}
}
int main()
{
scanf("%d",&s);
memset(dp,~0x3f,sizeof(dp));
for(int i=;i<=;i++)
dp[i][]=;
read();
int tot=dfs(,);
for(int i=tot;i>=;i--)
{
if(dp[][i]+s>)
{
cout<<i;
return ;
}
}
return ;
}
题目背景
神偷对艺术馆内的名画垂涎欲滴准备大捞一把。
题目描述
艺术馆由若干个展览厅和若干条走廊组成。每一条走廊的尽头不是通向一个展览厅，就
是分为两个走廊。每个展览厅内都有若干幅画，每副画都有一个价值。经过走廊和偷画都是
要耗费时间的。
警察会在n 秒后到达进口，在不被逮捕的情况下你最多能得到的价值。
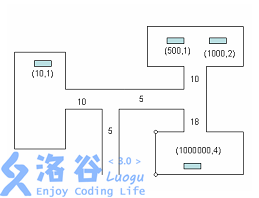
输入输出格式
输入格式：
第一行一个整数 n(n≤600)。
第二行若干组整数，对于每组整数（t,x），t 表示进入这个展览厅或经过走廊要耗费 t
秒的时间，若x>0 表示走廊通向的展览厅内有x 幅画,接下来
x对整数(w,c)表示偷一幅价值为 w 的画需要 c秒的时间。若
x=0 表示走廊一分为二。(t，c≤5; x≤30)
输入是按深度优先给出的。房间和走廊数不超过 300 个。
输出格式：
仅一个整数，表示能获得的最大价值。
输入输出样例
50
5 0 10 1 10 1 5 0 10 2 500 1 1000 2 18 1 1000000 4
1500 上一题的加强版，读入更加毒瘤，还要用到01背包。
读入的时候要在每一个房间做01背包，之后就和上一题一模一样了。
代码如下：
#include<iostream>
#include<cstring>
#include<cmath>
#include<string>
#include<cstdio>
using namespace std;
struct edge
{
int next;
int to;
int dis;
}g[];
int n,a=;
int num;
int aa,bb,cc;
int b[];
int dp[][];
int c[];
int last[];
void add(int,int,int);
void read(int faa)
{
scanf("%d%d",&aa,&bb);
add(faa,a+,aa*);
a++;
if(bb==)
{
faa=a;
read(faa);
read(faa);
}
else
{
for(int i=;i<=bb;i++)
{
scanf("%d%d",&b[i],&c[i]);
}
for(int i=;i<=bb;i++)
for(int j=n;j>=c[i];j--)
{
dp[a][j]=max(dp[a][j],dp[a][j-c[i]]+b[i]);//01背包
}
}
}
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
void dfs(int x)
{
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
dfs(v);
for(int j=n;j>=;j--)
for(int k=;k<=j;k++)
{
dp[x][j]=max(dp[x][j],dp[x][k]+dp[v][j-k-g[i].dis]);
}
}
}
int main()
{
scanf("%d",&n);
n--;
read();
dfs();
cout<<dp[][n];
return ;
}
三、树的重心问题
定义
- 树的重心：也叫树的质心。找到一个点,其所有的子树中最大的子树节点数最少,那么这个点就是这棵树的重心,删去重心后，生成的多棵树尽可能平衡。
性质
性质 1 ：树中所有点到重心的距离和是最小的，一棵树最多有两个重心（比如就两个点连个边）。
性质 2 ：把两棵树通过加一条边得到一颗新的树，新的树的重心必然在连接原来两棵树重心的路径上。
性质 3 ：一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
（这个重心的位置其实和边权是无关的） 证明不会，但记住就好，毕竟不会考
题目描述
有一个村庄居住着n个村民，有n-1条路径使得这n个村民的家联通，每条路径的长度都为1。现在村长希望在某个村民家中召开一场会议，村长希望所有村民到会议地点的距离之和最小，那么村长应该要把会议地点设置在哪个村民的家中，并且这个距离总和最小是多少？若有多个节点都满足条件，则选择节点编号最小的那个点。
输入输出格式
输入格式：
第一行。一个数n，表示有n个村民。
接下来n-1行，每行两个数字a和b，表示村民a的家和村民b的家之间存在一条路径。
输出格式：
一行输出两个数字x和y
x表示村长将会在哪个村民家中举办会议
y表示距离之和的最小
输入输出样例
4
1 2
2 3
3 4
2 4 这个题说白了就是求树的重心的单源最短路，最短路相信大家都会，这里不再赘述，关键是如何求出树的重心。
首先根据dfs序把无根树变成有根树
处理出以点u为根的子书的结点个数为s[u]（包括自己）
那么点u的所有的子树中最大的子树节点数就是
max{max{s[v]}(v是u的子节点）,n-s[u](这是因为是有根树前面没有算上“父节点”，这里考虑进来）}
void dfs(int fa,int x)
{
s[x]=;
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(x,v);
s[x]+=s[v];
maxx[x]=max(maxx[x],s[v]);
}
}
maxx[x]=max(maxx[x],n-s[x]);
}
然后再枚举所以的结点找出重心。之后跑一边最短路就行了
代码如下：
#include<iostream>
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<queue>
#define p pair<int,int>
#define pp make_pair
using namespace std;
priority_queue<p,vector< p >,greater< p > >q;
struct edge
{
int next;
int to;
int dis;
}g[];
int num,aa,bb,cc,an;
int ans;
int last[];
int s[];
int c[];
int d[];
int t,dd;
int n,m=;
int maxx[];
void dfs(int fa,int x)
{
s[x]=;
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(x,v);
s[x]+=s[v];
maxx[x]=max(maxx[x],s[v]);
}
}
maxx[x]=max(maxx[x],n-s[x]);
}
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int main()
{
cin>>n;
for(int i=;i<n;i++)
{
scanf("%d%d",&aa,&bb);
add(aa,bb,);
add(bb,aa,);
}
dfs(,);
for(int i=;i<=n;i++)
if(maxx[i]<m)
{
m=maxx[i];
an=i;
}
cout<<an;
memset(c,0x7f,sizeof(c));
c[an]=;
q.push(pp(,an));
while(q.size())
{
int t=q.top().second;
int dd=q.top().first;
q.pop();
if(d[t]) continue;
d[t]=;
for(int i=last[t];i;i=g[i].next)
{
int v=g[i].to;
int m=g[i].dis+dd;
if(c[v]>m)
{
c[v]=m;
q.push(pp(c[v],v));
}
}
}
for(int i=;i<=n;i++)
{
ans+=c[i];
}
cout<<" "<<ans;
return ;
}
洛谷 P2986 [USACO10MAR]伟大的奶牛聚集Great Cow Gat…
这题和上道题差不多，就是多了点权和边权，需要做一些小小的改动。
首先我们先找出树的重心，但是这里有点权啊，我们怎么办呢？其实我们只要在初始化的时候把点权加进去就好了呀。
void dfs(int x,int fa)
{
s[x]=a[x];//初始化为当前点的点权
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(v,x);
s[x]+=s[v];
maxx[x]=max(maxx[x],s[v]);
}
}
maxx[x]=max(maxx[x],sum-s[x]);//这里用所以点的点权和来作差
}
其实也就改了两个地方。最后算出最短路再乘上相应的点权即可。
代码如下：
#include<iostream>
#include<cmath>
#include<string>
#include<cstring>
#include<cstdio>
#include<queue>
#define p pair<long long,int>
#define pp make_pair
using namespace std;
priority_queue<p,vector< p >,greater< p > >q;
struct edge
{
int next;
int to;
int dis;
}g[];
int n;
long long anss;
int ans=;
int an;
int last[];
int s[];
int maxx[];
long long c[];
int d[];
long long a[];
int num,t;
int sum;
long long dd;
int aa,bb,cc;
void dfs(int x,int fa)
{
s[x]=a[x];//初始化为当前点的点权
for(int i=last[x];i;i=g[i].next)
{
int v=g[i].to;
if(v!=fa)
{
dfs(v,x);
s[x]+=s[v];
maxx[x]=max(maxx[x],s[v]);
}
}
maxx[x]=max(maxx[x],sum-s[x]);//这里用所以点的点权和来作差
}
void add(int from,int to,int dis)
{
g[++num].next=last[from];
g[num].to=to;
g[num].dis=dis;
last[from]=num;
}
int main()
{
scanf("%d",&n);
for(int i=;i<=n;i++)
{
scanf("%lld",&a[i]);
sum+=a[i];
}
for(int i=;i<n;i++)
{
scanf("%d%d%d",&aa,&bb,&cc);
add(aa,bb,cc);
add(bb,aa,cc);
}
dfs(,);
for(int i=;i<=n;i++)
{
if(maxx[i]<ans)
{
ans=maxx[i];
an=i;
}
}
memset(c,0x7f,sizeof(c));
c[an]=;
q.push(pp(,an));
while(q.size())
{
t=q.top().second;
dd=q.top().first;
q.pop();
if(d[t]) continue;
d[t]=;
for(int i=last[t];i;i=g[i].next)
{
int v=g[i].to;
long long m=g[i].dis+dd;
if(c[v]>m)
{
c[v]=m;
q.push(pp(c[v],v));
}
}
}
for(int i=;i<=n;i++)
{
anss+=a[i]*c[i];
}
cout<<anss;
return ;
}
树形dp入门我就写到这里，希望这篇文章对你有所帮助，有什么意见或者建议可以在下面评论 ，若是有什么不足的地方也欢迎指正。
树形dp 入门的更多相关文章
- POJ 2342 树形DP入门题
有一个大学的庆典晚会,想邀请一些在大学任职的人来參加,每一个人有自己的搞笑值,可是如今遇到一个问题就是假设两个人之间有直接的上下级关系,那么他们中仅仅能有一个来參加,求请来一部分人之后,搞笑值的最大是 ...
- 树形DP入门详解+题目推荐
树形DP.这是个什么东西?为什么叫这个名字?跟其他DP有什么区别? 相信很多初学者在刚刚接触一种新思想的时候都会有这种问题. 没错,树形DP准确的说是一种DP的思想,将DP建立在树状结构的基础上. 既 ...
- [poj2342]Anniversary party树形dp入门
题意:选出不含直接上下司关系的最大价值. 解题关键:树形dp入门题,注意怎么找出根节点,运用了并查集的思想. 转移方程:dp[i][1]+=dp[j][0];/i是j的子树 dp[i][0]+=max ...
- LuoGu-P1122 最大子树和+树形dp入门
传送门 题意:在一个树上,每个加点都有一个值,求最大的子树和. 思路:据说是树形dp入门. 用dfs,跑一边,回溯的时候求和,若和为负数,则减掉,下次不记录这个节点. #include <ios ...
- （树形DP入门题）Anniversary party（没有上司的舞会） HDU - 1520
题意: 有个公司要举行一场晚会.为了让到会的每个人不受他的直接上司约束而能玩得开心,公司领导决定:如果邀请了某个人,那么一定不会再邀请他的直接的上司,但该人的上司的上司,上司的上司的上司等都可以邀请. ...
- hdu_Anniversary party_(树形DP入门题)
题目连接:http://acm.hdu.edu.cn/showproblem.php?pid=1520 题意:有N个人,N-1个人有自己的上司,每个人有一个快乐值,如果这个人参加了聚会,那么这个人的直 ...
- 树形DP入门题目推荐以及解析
关于树形DP几道入门题目 今天恶补树形DP,感觉海星. 其实挺简单的. 介绍几道例题,我会的. 1.洛谷P1352 没有上司的舞会 我的一篇题解 我们可以考虑每一个节点都是有两种情况. 一个是被邀请: ...
- 树形DP入门学习
这里是学习韦神的6道入门树形dp进行入门,本来应放在day12&&13里,但感觉这个应该单独放出来好点. 这里大部分题目都是参考的韦神的思想. A - Anniversary part ...
- HDU 1561 树形DP入门
The more, The Better Time Limit: 6000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Oth ...
随机推荐
- 第23月第24天 git命令 .git-credentials git rm --cached git stash clear
在git push的时候,有时候我们会想办法撤销git commit的内容 1.找到之前提交的git commit的id git log 找到想要撤销的id 2.git reset –hard id ...
- Flume配置Failover Sink Processor
1 官网内容 2 看一张图一目了然 3 详细配置 source配置文件 #配置文件: a1.sources= r1 a1.sinks= k1 k2 a1.channels= c1 #负载平衡 a1.s ...
- Spring Boot Endpoint
Spring Boot 的 Endpoints 带着强烈的 DevOps 色彩, “you build it, you run it” ,开发不仅要关心如何实现功能,还需要关心服务在线上运行的状态,如 ...
- 🍓 JRoll、React滑动删除 🍓
import React, { Component } from 'react'; import '../src/css/reset.css'; import '../src/css/delete.c ...
- java实现在线浏览PDF文档功能
实现在线浏览pdf文档功能(本代码适用于项目服务中固定的并且少量的pdf浏览,比如注册时的注册条款在线浏览等): //设置响应内容类型为PDF类型 response.setContentType(&q ...
- vue2.0安装
vue2.0环境安装 参考网站http://www.open-open.com/lib/view/open1476240930270.html (以上博客vue init webpack-simple ...
- 创建 Pull Request
Pull Request 是开发者使用 GitHub 进行协作的利器.这个功能为用户提供了友好的页面,让提议的更改在并入官方项目之前,可以得到充分的讨论. 最简单地来说,Pull Request 是一 ...
- Hadoop环境准备
1． 集群简介 HADOOP集群具体来说包含两个集群:HDFS集群和YARN集群,两者逻辑上分离,但物理上常在一起. HDFS集群负责海量数据的存储,集群中的角色主要有: NameNode.DataN ...
- graph slam BACK END 相关技术资料收集
学习SLAM首推2个网站: 1. WIKI上的SLAM介绍与资源总结:http://en.wikipedia.org/wiki/Simultaneous_localization_and_mappin ...
- P3168 [CQOI2015]任务查询系统
题目地址:P3168 [CQOI2015]任务查询系统 主席树的模板题 更模板的在这儿:P3834 [模板]可持久化线段树 1(主席树) 形象的说,P3834是"单点修改,区间查询" ...