解救小哈——DFS算法举例

一、问题引入

有一天，小哈一个人去玩迷宫。但是方向感不好的小哈很快就迷路了。小哼得知后便去解救无助的小哈。此时的小哼已经弄清楚了迷宫的地图，现在小哼要以最快的速度去解救小哈。那么，问题来了...

二、问题的分析

首先我们用一个二维数组来存储这个迷宫，刚开始的时候，小哼处于迷宫的入口处（1,1），小哈在（p,q）。其实这道题的的本质就在于找从（1,1）到（p,q）的最短路径。

此时摆在小哼面前的路有两条，我们可以先让小哼往右边走，直到走不通的时候再回到这里，再去尝试另外一个方向。

在这里我们规定一个顺序，按照顺时针的方向来尝试（即右→下→左→上）。

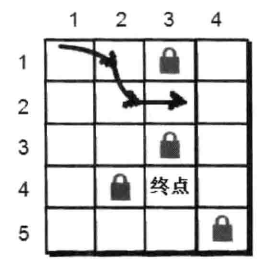
我们先来看看小哼一步之内可以到达的点有哪些？只有（1,2）和（2,1）。

根据刚才的策略，我们先往右边走，但右边（1,3）有障碍物，所以只能往下（2,2）这个点走。但是小哈并不在（2,2）这个点上，所以小哼还得继续往下走，直至无路可走或者找到小哈为止。

注意：并不是让我们找到小哈此题就解决了。因为刚才只是尝试了一条路的走法，而这条路并不一定是最短的。刚才很多地方在选择方向的时候都有多种选择，因此我们需要返回到这些地方继续尝试往别的方向走，直到把所有可能都尝试一遍，最后输出最短的一条路径。

例如下图就是一条可行的搜索路径：

三、解决问题——深度优先搜索

（1）如何写dfs函数。

dfs函数的功能是解决当前应该怎么办。而小哼处在某个点的时候需要处理的是：先检查小哼是否已经到达小哈的位置，如果没有到达则找出下一步可以走的地方。

为了解决这个问题，此处dfs()函数只需要维护三个参数，分别是当前这个点的x坐标，y坐标以及当前已经走过的步数step。

//dfs函数定义如下：
void dfs(int x,int y,int step)
{
    return ;
} 

（2）判断是否已经到达小哈的位置。

只需要判断当前的坐标是否与小哈的坐标相等就可以了，如果相等就标明已经到达小哈的位置。

void dfs(int x,int y,int step)
{
    if(x==p && y==q)  //判断是否到达小哈的位置
    {
        if(step<min)
            min=step;  //更新最小值
        return; //这步很重要！
    }
    return ;
} 

（3）如何获得下一个方向的坐标（此处定义一个方向数组）。

    int next[][]={
    {,},//向右走
    {,},//向下走
    {,-},//向左走
    {-,},//向上走
    };

通过这个方向数组，使用循环就可以方便地得到下一步的坐标。

这里将下一步的横坐标用tx存储，纵坐标用ty存储。

    for(k=;k<=;k++)
    {
        /*计算下一个点的坐标*/
        tx=x+next[k][];
        ty=y+next[k][];
    }

（4）对下一个点（tx,ty）进行判断（是否越界，是否有障碍物，是否已经在路径中）。

在这里我们用book[tx][ty]来记录格子[tx][ty]是否已经在路径中。

如果这个点符合所有的要求，就对这个点进行下一步的扩展，即dfs(tx,ty,step+1)。

注意这里是step+1，因为一旦从这个点开始继续往下尝试，就意味着步数已经增加了1。

    for(k=;k<=;k++)
    {
        /*计算下一个点的坐标*/
        tx=x+next[k][];
        ty=y+next[k][];
        if(tx< || tx>n || ty< || ty>m)  //判断是否越界
            continue;
        /*判断该点是否为障碍物或者已经在路径中*/
        if(a[tx][ty]== && book[tx][ty]==)
        {
            book[tx][ty]=;  //标记这个点已经走过
            dfs(tx,ty,step+);  //开始尝试下一个点
            book[tx][ty]=;  //尝试结束，取消这个点的标记
        }
    }

四、完整代码

#include<stdio.h>
int n,m,p,q,min=;
int a[][],book[][];
void dfs(int x,int y,int step)
{
    int next[][]={
    {,},//向右走
    {,},//向下走
    {,-},//向左走
    {-,},//向上走
    };
    int tx,ty,k;
    if(x==p && y==q)  //判断是否到达小哈的位置
    {
        if(step<min)
            min=step;  //更新最小值
        return;
    }
    /*枚举四种走法*/
    for(k=;k<=;k++)
    {
        /*计算下一个点的坐标*/
        tx=x+next[k][];
        ty=y+next[k][];
        if(tx< || tx>n || ty< || ty>m)  //判断是否越界
            continue;
        /*判断该点是否为障碍物或者已经在路径中*/
        if(a[tx][ty]== && book[tx][ty]==)
        {
            book[tx][ty]=;  //标记这个点已经走过
            dfs(tx,ty,step+);  //开始尝试下一个点
            book[tx][ty]=;  //尝试结束，取消这个点的标记
        }
    }
    return;
} 

int main()
{
    int i,j,startx,starty;
    scanf("%d %d",&n,&m);  //读入n和m，n为行，m为列
    /*读入迷宫*/
    for(i=;i<=n;i++)
        for(j=;j<=m;j++)
            scanf("%d",&a[i][j]);
    scanf("%d %d %d %d",&startx,&starty,&p,&q);  //读入起点和终点坐标
    /*从起点开始搜索*/
    book[startx][starty]=;  //标记起点已经在路径中，防止后面重复走
    dfs(startx,starty,);  //第一个参数是起点的x坐标，以此类推是起点的y坐标，初始步数为0
    printf("%d",min);  //输出最短步数
    return ;
}

五、写在最后

发明深度优先算法的是John E.Hopcroft 和 Robert E.Tarjan。他们并不是研究全排列或者迷宫问题时发明了这个算法。

1971~1972年，他们在斯坦福大学研究图的连通性（任意两点是否可以相互到达）和平面性（图中所有的边相互不交叉。在电路板上设计布线的时候，要求线与线不能交叉，这就是平面性的一个实际应用），发明了这个算法。他们也因此获得了1986年的图灵奖。

在授奖仪式上，当年全国象棋程序比赛的优胜者说他的程序用的就是深度优先搜索算法，这是以其制胜的关键。

通过本次学习，我明白了当我们遇到这种需要“分身”，需要不断尝试完成的事情时，可以尝试使用深度优先搜索算法，因为计算机的运算速度还是很强的，我们要借助他的优势，完成一些生活中比较繁琐重复的事情。

（注：文章内容源自 啊哈磊的《啊哈算法》——很有意思的一本算法入门书！）