[NN] 对于BackPropagation(BP, 误差反向传播)的一些理解

本文大量参照 David E. Rumelhart, Geoffrey E. Hinton and Ronald J. Williams, Learning representation by back-propagating errors, Nature, 323(9): 533-536, 1986.

在现代神经网络中, 使用最多的算法当是反向传播(BP). 虽然BP有着收敛慢, 容易陷入局部最小等缺陷, 但其易用性, 准确度却是其他算法无可比拟的.

在本文中, $w_{ji}$为连接前一层$unit_{i}$和后一层$unit_{j}$的权值.

---

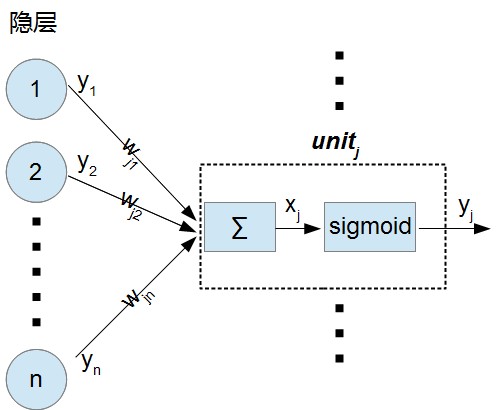
在MLP中, 对于输出层神经元$unit_{j}$, 它的输入$x_{j}$按下式进行计算(忽略偏置):

$x_{j} = \sum_{i} y_{i} w_{ji}$

可以看到它的输入等于前一层所有神经元的输出$y_{i}$和对应连接的加权和, 如上图

而$unit_{j}$的输出按下式计算:

$y_{j} = \frac{1}{1+e^{-x_{j}}}$. 这就是一个非线性变换sigmoid,

对于有监督训练, 期望输出$d$和实际输出$y$现在都是已知的, 定义误差为:

$E=\frac{1}{2}\sum_{c} \sum_{j}(y_{j,c}-d_{j,c})^2$

其中的$c$是输入-输出样本对的标号, $j$是输出层神经元的标号.

为求出$\partial E/\partial w_{ji}$,

我们先求$\partial E/\partial y_{j}$(之后就知道为何如此):

$\partial E/\partial y_{j} = y_{j} - d_{j}$, 此为误差$E$对神经元$unit_{j}$输出的偏导.

由链式法则:

$\partial E/\partial x_{j} = \partial E/\partial y_{j} * d y_{j}/d x_{j}$, 及上面的输入输出的关系式

$d y_{j}/d x_{j} = (\frac{1}{1+e^{-x_{j}}})' = \frac{e^{-x_{j}}}{(1+e^{-x_{j}})^{2}} = y_{j} * (1-y_{j})$

我们可以求出误差$E$对$unit_{j}$的输入$x_{j}$的偏导:

$\partial E/\partial x_{j} = \partial E/\partial y_{j} * y_{j} * (1-y_{j})$

至此, 我们得到了误差$E$对于$unit_{j}$输入$x_{j}$的偏导, 但网络训练的是权值(偏置), 所以我们必须知道$E$对于$w_{ji}$的偏导表达式.

同样由链式法则:

$\partial E/\partial w_{ji} = \partial E/\partial x_{j} * \partial x_{j}/\partial w_{ji}$, 及本层输入和权值的关系式:

$x_{j} = \sum_{i} y_{i} w_{ji}$, 可得 $\partial x_{j}/\partial w_{ji} = y_{i}$, 即:

$\partial E/\partial w_{ji} = \partial E/\partial x_{j} * y_{i}$,

其中$y_{i}$为前一层神经元$unit_{i}$的输出, $y_{j}$为后一层神经元$unit_{j}$的输出.

为了处理中间层, 我们同样是按照链式法则, 对于第i个神经元, 我们可以求得误差$E$对其输出$y_{i}$的梯度(注意这里是$y_{i}$, 不是$y_{j}$):

$\partial E/\partial y_{i} = \partial E/\partial x_{j} * \partial x_{j}/\partial y_{i} = \partial E/\partial x_{j} * w_{ji}$,

考虑到第i个神经元的所有连接, 可以得到:

$\partial E/\partial y_{i} = \sum_{j}\partial E/\partial x_{j} * w_{ji}$ (1)

这里的$\partial E/\partial x_{j}$为误差对于后一层的神经元$unit_{j}$输入$x_{j}$的偏导.

---

我们梳理一下:

对于连接神经元$i$和神经元$j$的权值$w_{ji}$, 主要有3个偏导分子, 输入$x_{j}$, 输出$y_{j}$和权值$ w_{ji}$, 他们的关系如下:

$\partial E/\partial x_{j} = \partial E/\partial y_{j} * y_{j} * (1-y_{j})$ (2)[基于$y_{j}$和$x_{j}$的非线性转换关系式];

$\partial E/\partial w_{ji} = \partial E/\partial x_{j} * y_{i}$ (3)[基于$x_{j}$和$y_{i}$的加权求和公式].

为求得上面的式(3), 我们需要求得$\partial E/\partial x_{j}$, 而为求得$\partial E/\partial x_{j}$, 需要求得$\partial E/\partial y_{j}$.

对于输出层(最后一层), $\partial E/\partial y_{j}=y_{j} - d_{j}$;

对于中间层, $\partial E/\partial y_{i}$按式(1)进行计算, 而式(1)中的$\partial E/\partial x_{j}$是由$\partial E/\partial y_{j}=y_{j} - d_{j}$算出来的. 当我们算出中间层的$\partial E/\partial y_{i}$之后, 把式(2)中的$y_{j}$全部替换成$y_{i}$就可以计算出$\partial E/\partial x_{i}$从而计算出式(3), 注意此时的式(3)中的$y_{i}$应该变为第i个神经元的前一层的对应神经元.

如此迭代, 我们就可以更新所有的权值啦.

权值调整的公式如下:

$\delta w = -\epsilon \partial E/\partial w$

---

总结:

BP的精髓: 如何通过链式法则求出$\partial E/\partial w_{ji}$

求法:

注意, 以下推导, 统一使用$i$ 作为当前层前一层的神经元下标, $j$ 作为当前层的神经元下标, $k$ 作为后一层神经元下标.

对于最后一层:

$\partial E/\partial w_{ji} = \partial E/\partial x_{j} * \partial x_{j}/\partial w_{ji}$ (1)

其中,

$\partial E/\partial x_{j} = \partial E/\partial y_{j} * \partial  y_{j}/\partial x_{j}$ (2)

$\partial x_{j}/\partial w_{ji} = y_{i}$ (3, 已求出, 谢谢背锅侠指正)

式(2)中,

$ \partial E/\partial y_{j} = y_{j} - d_{j}$ (已求出)

$ \partial y_{j}/\partial x_{j} = y_{j} * (1 - y_{j})$ (已求出)

从而计算出误差对[最后一层到倒数第二层的权值]的梯度.

$\partial E/\partial w_{ji} = ( y_{j} - d_{j}) * y_{j} * (1 - y_{j}) * y_{i}$

对于倒数第二层:

唯一变化的只有 $ \partial E/\partial y_{j} $ 的求法. 同样适用链式法则展开:

$ \partial E/\partial y_{j} =  \partial E/\partial y_{k} * \partial y_{k}/\partial y_{j}$, 其中 $y_{k}$ 为后一层(最后一层)的第$k$个神经元输出.

由于$\partial E/\partial y_{k} = y_{k} - d_{k}$(非固定, 每层表达式取前一层计算结果),

而$\partial y_{k}/\partial y_{j} = \partial y_{k}/\partial x_{k} * \partial x_{k}/\partial y_{j}$,

其中 $\partial y_{k}/\partial x_{k} = y_{k} * (1 -  y_{k})$ (固定的, 每层表达式都一样)

$\partial x_{k}/\partial y_{j} = w_{kj}$ (固定的, 每层表达式都一样)

故$\partial y_{k}/\partial y_{j} =  y_{k} * (1 - y_{k}) * w_{kj}$ (固定的, 每层表达式都一样)

从而有 $ \partial E/\partial y_{j} =  \partial E/\partial y_{k} * y_{k} * (1 -  y_{k}) * w_{kj}$ (非固定, 用于下一层的误差梯度计算)

最终: $\partial E/\partial w_{ji} = \partial E/\partial y_{j} * y_{j} * (1 - y_{j}) * y_{i}$

倒数第三层

可将倒数第二层求出的的$\partial E/\partial y_{j}$作为本层的$\partial E/\partial y_{k}$, 可计算出 $\partial E/\partial y_{j}$, 从而计算出 $\partial E/\partial w_{ji}$.