[算法整理]树上求LCA算法合集

1#树上倍增

　　以前写的博客:http://www.cnblogs.com/yyf0309/p/5972701.html

　　预处理时间复杂度O(nlog₂n)，查询O(log₂n),也不算难写。

2#st表(RMQ)

　　首先对一棵树进行dfs,得到欧拉序列，记录下每个节点的第一次出现位置。

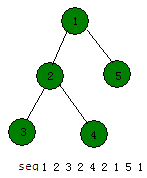
　　（先序遍历这棵树，访问到的节点(无论是从深的一层返回还是父节点访问)就加入到序列中，序列长度为2 * n - 1）

　　根据欧拉序列神奇的特性，两个点第一次出现的位置之间，深度最小的一个点，是这两个点LCA（反正我是不会证明）。于是可以干什么呢？就建st表就行了。

　　预处理时间复杂度O(2nlog₂(2n) + n)，查询时间复杂度O(log₂n)。

codevs 商务旅行:

 /**
  * codevs
  * Problem#1036
  * Accepted
  * Time:52ms
  * Memory:2736k
  */
 #include<iostream>
 #include<sstream>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cstring>
 #include<cctype>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #include<algorithm>
 #ifndef    WIN32
 #define    AUTO "%I64d"
 #else
 #define AUTO "%lld"
 #endif
 using namespace std;
 typedef bool boolean;
 #define smin(a, b) (a) = min((a), (b))
 #define smax(a, b) (a) = max((a), (b))
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         aFlag = -;
         x = getchar();
     }
     for(u = x - ''; isdigit((x = getchar())); u = u *  + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 template<typename T>class Matrix{
     public:
         T *p;
         int lines;
         int rows;
         Matrix():p(NULL){    }
         Matrix(int rows, int lines):lines(lines), rows(rows){
             p = new T[(lines * rows)];
         }
         T* operator [](int pos){
             return (p + pos * lines);
         }
 };
 #define matset(m, i, s) memset((m).p, (i), (s) * (m).lines * (m).rows)

 ///map template starts
 typedef class Edge{
     public:
         int end;
         int next;
         Edge(const int end = , const int next = ):end(end), next(next){}
 }Edge;
 typedef class MapManager{
     public:
         int ce;
         int *h;
         Edge *edge;
         MapManager(){}
         MapManager(int points, int limit):ce(){
             h = new int[(const int)(points + )];
             edge = new Edge[(const int)(limit + )];
             memset(h, , sizeof(int) * (points + ));
         }
         inline void addEdge(int from, int end){
             edge[++ce] = Edge(end, h[from]);
             h[from] = ce;
         }
         inline void addDoubleEdge(int from, int end){
             addEdge(from, end);
             addEdge(end, from);
         }
         Edge& operator[] (int pos) {
             return edge[pos];
         }
 }MapManager;
 #define m_begin(g, i) (g).h[(i)]
 ///map template ends

 int n, m;
 int cnt = ;
 Matrix<int> st;
 int* seq;
 int *dep, *app;
 MapManager g;
 const int P = ;
 int *mlog2;

 inline void init() {
     readInteger(n);
     g = MapManager(n,   * n);
     seq = new int[(const int)( * n + )];
     dep = new int[(const int)(n + )];
     app = new int[(const int)(n + )];
     for(int i = , a, b; i < n; i++){
         readInteger(a);
         readInteger(b);
         g.addDoubleEdge(a, b);
     }
     dep[] = ;
 }

 void dfs(int node, int f) {
     seq[++cnt] = node;
     dep[node] = dep[f] + ;
     app[node] = cnt;
     for(int i = m_begin(g, node); i != ; i = g[i].next) {
         int& e = g[i].end;
         if(e == f)    continue;
         dfs(e, node);
         seq[++cnt] = node;
     }
 }

 inline void init_log() {
     mlog2 = new int[(const int)( * n + )];
     mlog2[] = ;
     for(int i = ; i <=  * n; i++)
         mlog2[i] = mlog2[i / ] + ;
 }

 inline void init_st() {
     init_log();
     st = Matrix<int>(cnt, mlog2[cnt] + );
     for(int i = ; i <= cnt; i++)
         st[i][] = seq[i];//,cout << i << " " << 0 << ":" << st[i][0] << endl;
     for(int j = ; j <= P; j++)
         for(int i = ; i + ( << j) -  <= cnt; i++)
             st[i][j] = (dep[st[i][j - ]] < dep[st[i + ( << (j - ))][j - ]]) ? (st[i][j - ]) : (st[i + ( << (j - ))][j - ]);
 //            cout << i << " " << j << ":" << st[i][j] << endl;
 }

 inline int lca(int a, int b) {
     if(app[a] > app[b])    swap(a, b);
     int pos = mlog2[app[b] - app[a] + ];
     int u = st[app[a]][pos];
     int v = st[app[b] - ( << pos) + ][pos];
     return (dep[u] > dep[v]) ? (v) : (u);
 }

 int last;
 int dist;
 inline void solve() {
     readInteger(m);
     readInteger(last);
     for(int i = , a; i < m; i++){
         readInteger(a);
         int l = lca(a, last);
         dist += dep[a] + dep[last] -  * dep[l];
         last = a;
     }
     printf("%d", dist);
 }

 int main() {
     init();
     dfs(, );
     init_st();
     solve();
     return ;
 }

商务旅行(st表)

3#Tarjan算法（离线算法）

　　Tarjan需要一个并查集来辅助。

　　算法思路大概是这样:

　　init:初始化并查集，对查询建一个邻接链表，还是按照存边的方式，要双向的,再用一个数组记录第i个询问是否解决了。

　　1.访问子树

　　2.每次访问结束后将子树的并查集中的父节点指向当前节点。

　　3.子树都访问完了后，开始处理以该节点为起点的询问，如果终点已经被访问过了并且没有被解决，那么这个点和终点的LCA是终点在并查集中的父节点，然后再记录是否解决的那个数组中把对应位置设上true。

　　（画画图，还是很容易理解的）

 #include<iostream>
 #include<sstream>
 #include<cstdio>
 #include<cmath>
 #include<cstdlib>
 #include<cstring>
 #include<cctype>
 #include<queue>
 #include<set>
 #include<map>
 #include<stack>
 #include<vector>
 #include<algorithm>
 #ifndef    WIN32
 #define    AUTO "%I64d"
 #else
 #define AUTO "%lld"
 #endif
 using namespace std;
 typedef bool boolean;
 #define smin(a, b) (a) = min((a), (b))
 #define smax(a, b) (a) = max((a), (b))
 template<typename T>
 inline void readInteger(T& u){
     char x;
     int aFlag = ;
     while(!isdigit((x = getchar())) && x != '-');
     if(x == '-'){
         aFlag = -;
         x = getchar();
     }
     for(u = x - ''; isdigit((x = getchar())); u = u *  + x - '');
     ungetc(x, stdin);
     u *= aFlag;
 }

 typedef class Edge {
     public:
         int end;
         int next;
         int w;
         Edge(const int end = , const int next = , const int w = ):end(end), next(next), w(w){        }
 }Edge;

 typedef class MapManager{
     public:
         int ce;
         Edge* edges;
         int* h;
         MapManager():ce(), edges(NULL), h(NULL){        }
         MapManager(int points, int limit):ce(){
             edges = new Edge[(const int)(limit + )];
             h = new int[(const int)(points + )];
             memset(h, , sizeof(int) * (points + ));
         }
         inline void addEdge(int from, int end, int w){
             edges[++ce] = Edge(end, h[from], w);
             h[from] = ce;
         }
         inline void addDoubleEdge(int from, int end, int w){
             addEdge(from, end, w);
             addEdge(end, from, w);
         }
         Edge& operator [](int pos){
             return edges[pos];
         }
 }MapManager;
 #define m_begin(g, i) (g).h[(i)]

 typedef class union_found{
     public:
         int *f;
         union_found():f(NULL) {}
         union_found(int points) {
             f = new int[(const int)(points + )];
         }
         int find(int x) {
             if(f[x] != x)    return f[x] = find(f[x]);
             return f[x];
         }
         void unit(int fa, int so) {
             int ffa = find(fa);
             int fso = find(so);
             f[fso] = ffa;
         }
         int& operator [](int pos){
             return f[pos];
         }
 }union_found;

 int n, m;
 MapManager g;
 MapManager q;
 int *results;
 boolean* enable;
 int *querya, *queryb;
 union_found uf;
 boolean* visited;
 int* dist;

 inline void init(){
     readInteger(n);
     g = MapManager(n,  * n);
     for(int i = , a, b, c; i < n; i++){
         readInteger(a);
         readInteger(b);
         readInteger(c);
         g.addDoubleEdge(a, b, c);
     }
     readInteger(m);
     q = MapManager(n,  * m);
     querya = new int[(const int)(m + )];
     queryb = new int[(const int)(m + )];
     results = new int[(const int)(m + )];
     enable = new boolean[(const int)(m + )];
     dist = new int[(const int)(n + )];
     uf = union_found(n);
     visited = new boolean[(const int)(n + )];
     memset(visited, false, sizeof(boolean) * (n + ));
     memset(enable, true, sizeof(boolean) * (m + ));
     for(int i = ; i <= m; i++){
         readInteger(querya[i]);
         readInteger(queryb[i]);
         q.addDoubleEdge(querya[i], queryb[i], i);
     }
     dist[] = ;
 }

 void tarjan(int node, int f){
     uf[node] = node;
     visited[node] = true;
     for(int i = m_begin(g, node); i != ; i = g[i].next){
         int& e = g[i].end;
         if(e == f)    continue;
         dist[e] = dist[node] + g[i].w;
         tarjan(e, node);
         uf[e] = node;
     }
     for(int i = m_begin(q, node); i != ; i = q[i].next) {
         int& e = q[i].end;
         if(visited[e] && enable[q[i].w]){
             int lca = uf.find(e);
             results[q[i].w] = lca;
             enable[q[i].w] = false;
         }
     }
 }

 inline void solve(){
     tarjan(, );
     for(int i = ; i <= m; i++){
         int dis = dist[querya[i]] + dist[queryb[i]] -  * dist[results[i]];
         printf("%d\n", dis);
     }
 }

 int main(){
     init();
     solve();
     return ;
 }

Tajan

4#树链剖分

　　详见:http://www.cnblogs.com/yyf0309/p/6344982.html

　　树链剖分的空间复杂度比上面任何一种方法都要优，所以当空间很紧的时候(当然，我相信出题人不会那么坑人)是不错的选择。