poj3347 Kadj Squares【计算几何】

Kadj Squares

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 3594		Accepted: 1456

Description

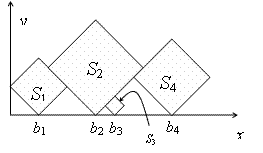
In this problem, you are given a sequence S₁, S₂, ..., S_n of squares of different sizes. The sides of the squares are integer numbers. We locate the squares on the positive x-y quarter of the plane, such that their sides make 45 degrees with x and y axes, and one of their vertices are on y=0 line. Let b_i be the x coordinates of the bottom vertex of S_i. First, put S₁ such that its left vertex lies on x=0. Then, put S₁, (i > 1) at minimum b_i such that

• b_i > b_i-1 and
• the interior of S_i does not have intersection with the interior of S₁...S_i-1.

The goal is to find which squares are visible, either entirely or partially, when viewed from above. In the example above, the squares S₁, S₂, and S₄ have this property. More formally, S_i is visible from above if it contains a point p, such that no square other than S_i intersect the vertical half-line drawn from p upwards.

Input

The input consists of multiple test cases. The first line of each test case is n (1 ≤ n ≤ 50), the number of squares. The second line contains n integers between 1 to 30, where the ith number is the length of the sides of S_i. The input is terminated by a line containing a zero number.

Output

For each test case, output a single line containing the index of the visible squares in the input sequence, in ascending order, separated by blank characters.

Sample Input

4
3 5 1 4
3
2 1 2
0

Sample Output

1 2 4
1 3

Source

Tehran 2006

题意：

n个正方形45度角的放，边靠着边，放完了之后从顶部往下看。有哪些正方形没有被挡住。

思路：

我们从这张图来看，正方形之间的三角形是等腰三角形，边长是两个正方形边长的较小值。

我们现在记下每个正方形的最左的横坐标，和最右的横坐标，和边长。并且我们假设输入的边长是实际边长投影在横坐标上的长度。

因为大家都同时放大，是不影响结果的。

当我们摆好了前面i-1个正方形之后，摆第i个正方形。那么可以知道第i个正方形的左端点应该是前面所有正方形的最右端点减去两个正方形边长之差。

摆好第i个正方形之后我们再看，前i-1个正方形中有哪几个被遮掉了一部分。

有两种情况，一种是左边的遮掉右边的，一种是右边的遮掉左边的。

 #include <iostream>
 #include <set>
 #include <cmath>
 #include <stdio.h>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <map>
 //#include <bits/stdc++.h>
 using namespace std;
 typedef long long LL;
 #define inf 0x7f7f7f7f

 const int maxn = ;
 int n;
 struct node{
     int len, l, r;
 }squ[maxn];

 int main()
 {
     while(scanf("%d", &n) != EOF && n){
         for(int i = ; i <= n; i++){
             scanf("%d", &squ[i].len);
             squ[i].l = ;
             for(int j = ; j < i; j++){
                 squ[i].l = max(squ[i].l, squ[j].r - abs(squ[i].len - squ[j].len));
             }
             squ[i].r = squ[i].l +  * squ[i].len;
             for(int j = ; j < i; j++){
                 if(squ[j].r > squ[i].l){
                     if(squ[i].len > squ[j].len){
                         squ[j].r = squ[i].l;
                     }
                     else{
                         squ[i].l = squ[j].r;
                     }
                 }
             }
         }

         bool flag = true;
         for(int i = ; i <= n; i++){
             if(squ[i].l < squ[i].r){
                 if(flag){
                     printf("%d", i);
                     flag = false;
                 }
                 else{
                     printf(" %d", i);
                 }
             }
         }
         printf("\n");

     }
     return ;
 }