【LeetCode】不同路径

如图，m × n 的网格的左上角作为起点，每次只能向右或向下移动一格，最终要到达右下角。求有多少条可能的路径。

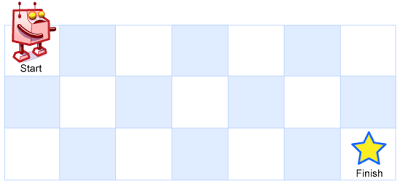
m，n 最大取 100。

我的想法是递归，分分钟实现

 int uniquePaths(int m, int n) {
     if (m ==  || n == )    return ;
     return uniquePaths(m - , n) + uniquePaths(m, n - );
 }

然而数字稍微取大（m = 19，n = 13）就 Time Limit Exceeded 了。

于是这么想，以上图 3 × 7 的网格为例，可以向下移动 2 格，向右移动 6 格，一共需要移动 8 格。那么只需要在 8 格中任意挑选 2 格作为向下移动，另外 6 格都向右即可。每种不同的选择表示了一条不同的路径。

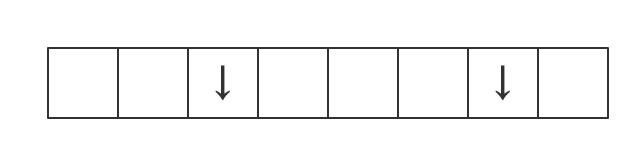
那么可以用排列组合公式。m 和 n 表示向右或向下移动的次数，第二个等号是为了减少计算次数，因为 m!、n!、(m+n)! 阶乘计算时重复计算了一些数字。

 int uniquePaths(int m, int n) {
     m--;    n--;
     int small = min(m, n), big = max(m, n);
     return fac(big + , big + small) / fac(, small);
 }
 /* 由于m、n能取到100，使用int计算连乘会溢出 */
 long long fac(int start, int end) {
     long long result = ;
     for (int i = start; i <= end; i++)
         result *= i;
     return result;
 }

同时注意到公式还可以继续化简，这样就只需要用一个循环语句。

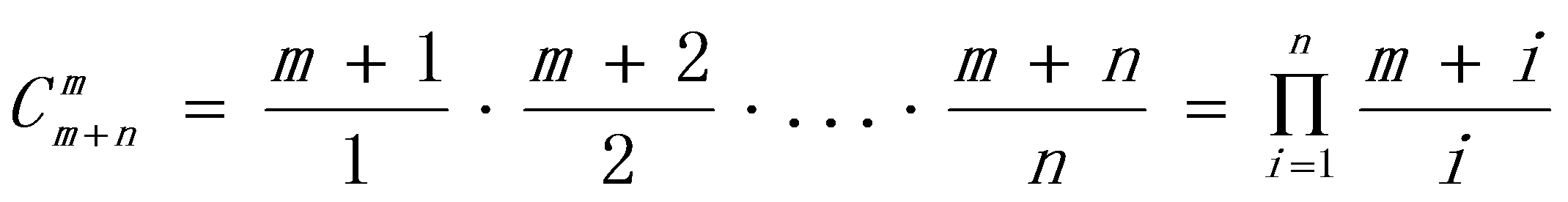
但这种算法用到了 n 次除法，得注意将计算结果存储在 double 型变量中，因为 int 型的 (m + i) / i 会得出一个整数结果而导致计算过程中数据错误。

如果定义 int result = 1，第 6 行为 result *= (big + i) / i，计算会出错。例如 m = 4，n = 4 时，会输出 16，而正确答案是 20。

即使将 result 改为 double 型，第 6 行改为 result *= (double)(big + i) / i，也会出错。例如 m = 10，n = 10 时，会输出 48619，而正确答案是 48620。

 int uniquePaths(int m, int n) {
     m--;    n--;
     int small = min(m, n), big = max(m, n);
     double result = 1.0;
     for (int i = ; i <= small; i++) {
         result = result * (big + i) / i;
     }
     return (int)result;
 }

因此输入输出均为 int 型的计算中，若计算过程用到多次很可能无法除尽的除法时，得非常小心。

方法二：

动态规划

这是一个基本的动态规划问题。

由于只能向右或向下移动，那么到达一个格子的时候只有可能是两种情况：

1. 从上边一格向下移动到这一格；
2. 从左边一格向右移动到这一格。

假设移动到 (i, j) 这一格的不同路径数为 P[i][j]，显然，P[i][j] = P[i - 1][j] + P[i][j - 1]。边界条件是最左边一列（无法从更左边移动过来）和最上边一行（无法从更上边移动过来），但显然对于所有 i，j 有 P[0][j] = 1，P[i][0] = 1。

 int uniquePaths(int m, int n) {
     vector<vector<int>> path(m, vector<int> (n, ));
     for (int i = ; i < m; i++)
         for (int j = ; j < n; j++)
             path[i][j] = path[i - ][j] + path[i][j - ];
     return path[m - ][n - ];
 }

这种算法的时间复杂度是 O(m * n)，空间复杂度也是 O(m * n)，效率较低。

注意到每次更新 P[i][j] 的值，只需要用到 P[i - 1][j]（同一列）和 P[i][j - 1]（左边一列），因此只需要维护两列元素而不需要维护整个 m × n 矩阵。

 int uniquePaths(int m, int n) {
     if (m > n)  return uniquePaths(n, m);    // 这种方法比比较 m、n 大小并交换或者取较大、较小值更高明！
     vector<int> left(n, ), right(n, );
     for (int i = ; i < m; i++) {
         for (int j = ; j < n; j++)
             right[j] = left[j] + right[j - ];
         swap(left, right);
     }
     return left[n - ];
 }

这种算法的空间复杂度优化到 O(min(m, n))。又发现，对两列执行完循环后移动到下面两列时，左边一列 left 就是上一轮 right 交换过来的，因此只需要维护一列即可。

 int uniquePaths(int m, int n) {
     if (m > n)  return uniquePaths(n, m);
     vector<int> path(n, );
     for (int i = ; i < m; i++) {
         for (int j = ; j < n; j++)
             path[j] += path[j - ];
     }
     return path[n - ];
 }