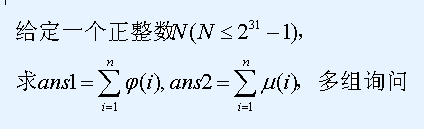2019.02.12 bzoj3944: Sum(杜教筛)
传送门
题意:
思路:直接上杜教筛。
知道怎么推导就很简单了,注意预处理的范围。
然后我因为预处理范围不对被zxyoi教育了(ldx你这个傻×两倍常数活该被卡TLE) 喜闻乐见
代码:
#include<bits/stdc++.h>
#define ri register int
using namespace std;
const int N=7500005,lim=7500000;
typedef long long ll;
namespace Sieve{
int pri[N],tot=0,mu[N];
ll phi[N];
bool vis[N];
map<int,int>mpa;
map<int,ll>mpb;
inline void init(){
vis[1]=phi[1]=mu[1]=1;
for(ri i=2;i<=lim;++i){
if(!vis[i])pri[++tot]=i,phi[i]=i-1,mu[i]=-1;
for(ri j=1;j<=tot&&i*pri[j]<=lim;++j){
vis[i*pri[j]]=1;
if(i==i/pri[j]*pri[j]){
phi[i*pri[j]]=pri[j]*phi[i],mu[i*pri[j]]=0;
break;
}
phi[i*pri[j]]=(pri[j]-1)*phi[i],mu[i*pri[j]]=-mu[i];
}
}
for(ri i=2;i<=lim;++i)phi[i]+=phi[i-1],mu[i]+=mu[i-1];
}
inline int Mu(const int&x){
if(x<=lim)return mu[x];
if(mpa[x])return mpa[x];
int ret=0;
for(ri l=2,r;r<x&&l<=x;l=r+1)r=x/(x/l),ret+=Mu(x/l)*(r-l+1);
return mpa[x]=1-ret;
}
inline ll Phi(const int&x){
if(x<=lim)return phi[x];
if(mpb[x])return mpb[x];
ll ret=0;
for(ri l=2,r;r<x&&l<=x;l=r+1)r=x/(x/l),ret+=Phi(x/l)*(r-l+1);
return mpb[x]=(ll)x*((ll)x+1)/2-ret;
}
}
int main(){
freopen("lx.in","r",stdin);
Sieve::init();
int tt,n;
scanf("%d",&tt);
while(tt--)scanf("%d",&n),cout<<Sieve::Phi(n)<<' '<<Sieve::Mu(n)<<'\n';
return 0;
}
2019.02.12 bzoj3944: Sum(杜教筛)的更多相关文章
- [BZOJ3944]Sum(杜教筛)
3944: Sum Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 6201 Solved: 1606[Submit][Status][Discuss ...
- [bzoj3944] sum [杜教筛模板]
题面: 传送门 就是让你求$ \varphi\left(i\right) $以及$ \mu\left(i\right) $的前缀和 思路: 就是杜教筛的模板 我们把套路公式拿出来: $ g\left( ...
- bzoj3944: Sum 杜教筛板子题
板子题(卡常) 也可能是用map太慢了 /************************************************************** Problem: 3944 Us ...
- 3944: Sum[杜教筛]
3944: Sum Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 3471 Solved: 946[Submit][Status][Discuss] ...
- 【Bzoj3944】杜教筛模板(狄利克雷卷积搞杜教筛)
题目链接 哇杜教筛超炫的 有没有见过$O(n^\frac{2}{3})$求欧拉函数前缀和的算法?没有吧?蛤蛤蛤 首先我们来看狄利克雷卷积是什么 首先我们把定义域是整数,陪域是复数的函数叫做数论函数. ...
- HDU6706 huntian oy(2019年CCPC网络赛+杜教筛)
目录 题目链接 思路 代码 题目链接 传送门 思路 看到这题还比较懵逼,然后机房大佬板子里面刚好有这个公式\(gcd(a^n-b^n,a^m-b^m)=a^{gcd(n,m)}-b^{gcd(n,m) ...
- 洛谷P4213 Sum(杜教筛)
题目描述 给定一个正整数N(N\le2^{31}-1)N(N≤231−1) 求ans_1=\sum_{i=1}^n\phi(i),ans_2=\sum_{i=1}^n \mu(i)ans1=∑i=1 ...
- bzoj 3944 Sum —— 杜教筛
题目:https://www.lydsy.com/JudgeOnline/problem.php?id=3944 杜教筛入门题! 看博客:https://www.cnblogs.com/zjp-sha ...
- BZOJ 3944: Sum [杜教筛]
3944: Sum 贴模板 总结见学习笔记(现在还没写23333) #include <iostream> #include <cstdio> #include <cst ...
随机推荐
- Bootstrap关闭当前页
function doBack() { var index = parent.layer.getFrameIndex(window.name); parent.lay ...
- day31网络编程
网络编程1. 目标:编写一个C/S架构的软件 C/S: Client(用户端)--------基于网络----------Server(服务端) B/S: Browser-------基于 ...
- python字符串前面的r/u/b的意义 (笔记)
u/U:表示unicode字符串 : 不是仅仅是针对中文, 可以针对任何的字符串,代表是对字符串进行unicode编码. r/R:非转义的原始字符串: 与普通字符相比,其他相对特殊的字符,其中可能包含 ...
- python:爬虫获取淘宝/天猫的商品信息
[需求]输入关键字,如书包,可以搜索出对应商品的信息,包括:商品标题.商品链接.价格范围:且最终的商品信息需要符合:包邮.价格差不会超过某数值 #coding=utf-8 ""&q ...
- Django模板语言相关内容 Djan
Django模板语言相关内容 Django模板系统 官方文档 常用语法 只需要记两种特殊符号: {{ }}和 {% %} 变量相关的用{{}},逻辑相关的用{%%}. 变量 {{ 变量名 }} ...
- php 处理上百万条的数据库如何提高处理查询速度
1.对查询进行优化,应尽量避免全表扫描,首先应考虑在 where 及 order by 涉及的列上建立索引. 2.应尽量避免在 where 子句中对字段进行 null 值判断,否则将导致引擎放弃使用索 ...
- 请求不同域的数据方法:requests Jsonp cors
在需要访问不同域的接口的数据的时候,一般有两种方式: 第一种: 使用requests模块,在业务逻辑中直接访问别的域的接口,获取数据,然后将返回的数据显示到前端页面上; 这个时候,数据访问的流程是: ...
- cmake 指定连接的opencv版本
我们通常需要使用不同版本的opencv,这时候如果用cmake构建工程,直接指定本地编译好的路径就可以,在CMakeLists.txt中添加: set(OpenCV_DIR "/xxx/wo ...
- VS2010 Chart控件(一)Chart控件在ASP.NET网站中的应用示例详解(C#语言)
步骤如下: 1. Chart控件(一)Chart控件在ASP.NET网站中的应用示例详解(C#语言)" title="VS2010 Chart控件(一)Chart控件在ASP.NE ...
- flume知识点总结
首先介绍一下在flume中常用的一个数据格式,以及使用该格式的优缺点: 从flume写数据到hdfs中的时候,使用二进制格式相对于使用纯文本来说是一种更好的选择,因为大多数二进制格式都有一些方法指明 ...