PJ可能会用到的动态规划选讲-学习笔记

by Pleiades_Antares

难度和速度全部都是按照普及组来定的咯

数位状压啥就先不讲了

这里主要提到的都是比较简单的DP

一道思维数学巧题（补昨天）

先看一道外文题目：

（简单翻译稍微改了下，原题目戳我）

现在PA要放技能，要放n(10e9)个技能，

但是放技能有冷却时间，x秒才能放一次。

PA有两个事情可以做：

有m个天赋可以学习，第i个天赋要花b[i]块钱，作用是把冷却时间改为a[i]。

可以找个打手，有k个打手可以找，请第i个打手需要花掉d[i]块钱，他会直接帮你放c[i]次技能。

m, k 10e5

给出初始金钱数，问所用的最少时间。

注意天赋最多只能学习一个，打手最多只能请一位。

拿到题目以后，我们首先要想：这道题用什么方法来做？（比如贪心，dp等等）

首先：

要枚举选择学哪个天赋（此时我们还剩下C块钱）

然后下一步➡️找到用哪个打手比较好。

看这张图，贪心显然是不行的。

那当我们枚举完以后怎么才能选择打手呢？

——什么情况下我们绝对不会选择x这个打手

——当且仅当：有人比x便宜且比x能干活

啥时候可以贪心呢？

我们把那种又贵又不好用“名不副实”的打手给排除掉

直接对打手按照花费排序，然后如果某个打手前面有（说明比他便宜）比他能干的，那么就说明这个人名不副实。

这样排除了以后，单调的时候，➡️打手越贵就越好用

这个时候我们再选择自己能力范围内能够买到的最贵的打手就可以了哇

此时处理非常容易，二分查找就直接ok

ll les(ll p)

{

    // printf("you can use %lld to less %lld\n",(*--upper_bound(ok.begin(),ok.end(),hero(0,p))).d,(*--upper_bound(ok.begin(),ok.end(),hero(0,p))).c);

    return (*(--upper_bound(ok.begin(),ok.end(),hero(0,p)))).c;

}

上面为二分查找orz rxz大佬写的我们这种蒟蒻就好好写正常的二分查找好了qwq

rxz大佬代码：

#include <cstdio>

#include <cstdlib>

#include <vector>

#include <cstring>

#include <algorithm>

using namespace std;

typedef long long ll;

ll a[100005],b[100005];

ll n,m,k,x,s;

struct hero

{

    ll c,d;

    friend bool operator < (hero a,hero b)

    {

        return a.d<b.d;

    }

    hero(ll _c=0,ll _d=0) {c=_c,d=_d;}

};

hero h[100005];

vector <hero> ok;

void inp()

{

    ll i;

    memset(a,0,sizeof(a));

    memset(b,0,sizeof(b));

    memset(h,0,sizeof(h));

    ok.clear();

    scanf("%lld%lld%lld%lld%lld",&n,&m,&k,&x,&s);

    for(i=1;i<=m;i++)

        scanf("%lld",&a[i]);

    for(i=1;i<=m;i++)

        scanf("%lld",&b[i]);

    for(i=1;i<=k;i++)

        scanf("%lld",&h[i].c);

    for(i=1;i<=k;i++)

        scanf("%lld",&h[i].d);

}

void gao()

{

    ll i,now=0;

    sort(h+1,h+1+k);

    ok.push_back(hero(0,0));

    for(i=1;i<=k;i++)

    {

        if(h[i].c<=now) continue;

        now=max(now,h[i].c);

        ok.push_back(h[i]);

    }

}

ll les(ll p)

{

    // printf("you can use %lld to less %lld\n",(*--upper_bound(ok.begin(),ok.end(),hero(0,p))).d,(*--upper_bound(ok.begin(),ok.end(),hero(0,p))).c);

    return (*(--upper_bound(ok.begin(),ok.end(),hero(0,p)))).c;

}

ll calc()

{

    ll i,t,ans=9000000000000000233;

    a[0]=x,b[0]=0;

    for(i=0;i<=m;i++)  //use talent i

        if(s>=b[i])

        {

            if(n-les(s-b[i])>0) t=(n-les(s-b[i]))*a[i];

            else t=0;

            // printf("Use talent %lld t=%lld\n",i,t);

            ans=min(ans,t);

        }

    printf("%lld\n",ans);

}

void work()

{

    inp();

    gao();

    calc();

}

int main(void)

{

    ll t;

    scanf("%lld",&t);

    while(t--)

        work();

    return 0;

}

DP选讲

DP是啥？

简单来说——哲学三连

我是谁？【设计状态】

我从哪里来？【从之前状态设计转移】

我到哪里去？【向之后状态设计转移】

热身：钢条切割

钢条长度为n，可以切割。

最后，对于每个长度k，有对应价值w[k]。

问切割结束以后，所有钢条的价值和最大是多少。

辅助理解灵魂绘图：

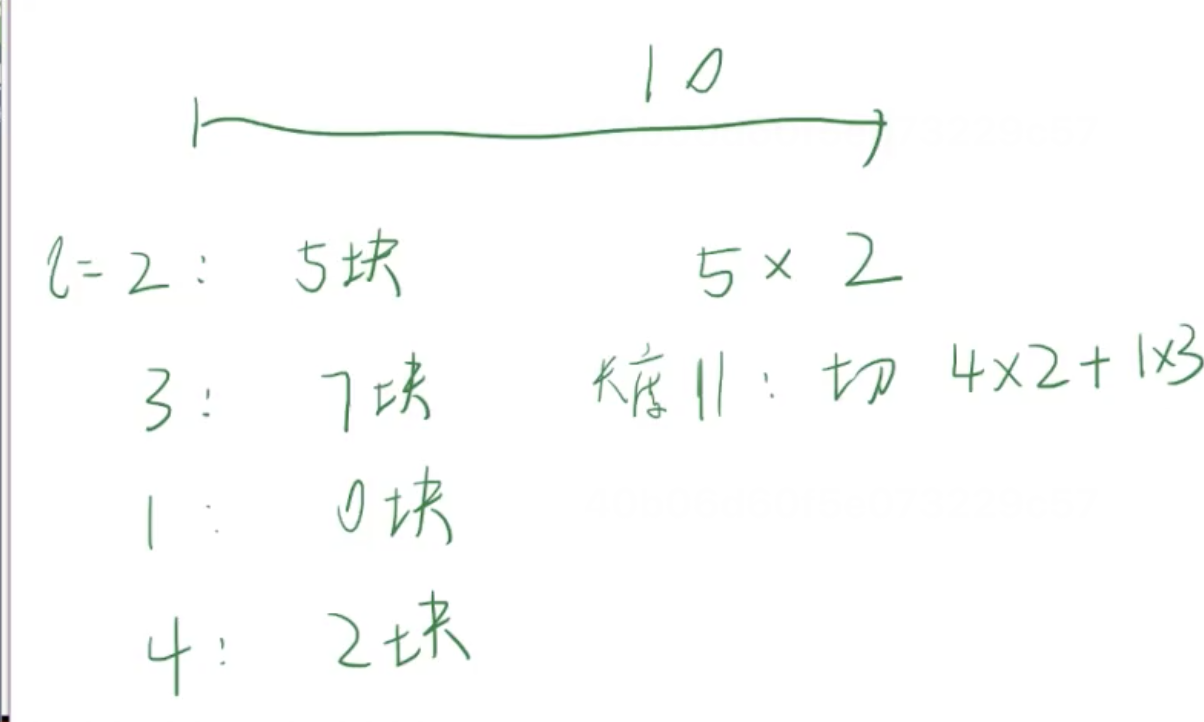
首先，按照哲学三连来分析一下。

状态：dp[i]表示在i剁了一刀，[1,i]这段区间产生的最大价值。

从哪里来：对于所有的k，dp[i-k]都能到达dp[i]

转移方程：dp[i]=max{dp[i-k+w[k]}

一些历年的NOIP普及组题目讲解

题表见此：

P1002:过河卒

状态： dp[i][j]表示路径数

dp[i][j]可以从dp[i-1][j]，dp[i][j-1]这里来

转移方程：dp[i][j]=dp[i-1][j]+dp[i][j-1]

考虑马

被马控制的点为0（不可能走到）

写一个特判：如果被控制那么就是0，否则就是刚才的那个转移方程。

过河卒属于是非常非常容易的一个dp，在考场上一定要能写出来。

P1048 采药

设计状态

dp[v]表示容量为v，装的最大价值（有后效性）（无后效性是指：某阶段的状态一旦确定，则此后过程的演变不再受此前各状态及决策的影响）

如果一个东西有后效性，把这个东西放进dp数组的下标往往可以消除后效性。

dp[k][v] 用时为v，考虑[1,k]的药。这样就可以排除其后效性。

我是谁：

dp[k][t]考虑了前k个药，用时恰好为t，所取得的最大价值。

我从哪里来：

1⃣️k这个药没有采 dp[k-1][t]

2⃣️k这个药采了 dp[k-1][t-a[k]]+w[k] 之前用掉的时间就是t-a[k]，（用a[k]的时间来采这个药）（付出了时间得到了价值）（

（3⃣️dp[k][t-1]来）

然后取一个max就做出来题目了。

单调队列

给一个数组a和一个正整数k

对于每一个长度为k的区间，求出这个区间内的最大值。

想

——如果一个选手比你小，还比你强，那你就打不过他了。（比如说洛谷新一代吉祥物chen_zhe先生）

题目

Dice Game

// https://vjudge.net/problem/Gym-101502D

#include <cstdio>

#include <cstdlib>

#include <algorithm>

using namespace std;

// dp[n][k] : score=n , k is up

int dp[10005][7];

void move(int n,int k)

{

    int ans,i,j;

    for(i=1;i<=6;i++)

        if(i!=k && i+k!=7)

            dp[n+i][i]=min(dp[n+i][i],dp[n][k]+1);

}

void calc()

{

    int i,j;

    for(i=0;i<=10002;i++)

        for(j=1;j<=6;j++)

            dp[i][j]=23333333;

    dp[0][1]=0;

    for(i=0;i<=10002;i++)

        for(j=1;j<=6;j++)

            move(i,j);

}

void get()

{

    int x,i,ans=23333333;

    scanf("%d",&x);

    for(i=1;i<=6;i++)

        ans=min(ans,dp[x][i]);

    printf("%d\n",ans==23333333?-1:ans);

}

int main(void)

{

    int t;

    calc();

    scanf("%d",&t);

    while(t--)

        get();

    return 0;

}

考前训练（复习）指南

只要你开的空间爆了不管你有没有用那么多都是一个死