B-Tree外存数据结构 _（B 树）第二部分

2. B 树

B 树是为了磁盘或其它存储设备而设计的一种多叉（相对于二叉，B树每个内结点有多个分支，即多叉）平衡查找树

一棵B树，一棵关键字为英语中辅音字母的B树，现在要从树中查找字母R（包含n[x]个关键字的内结点x，x有n[x]+1个子女（一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女），所有的叶结点都处于相同的深度，带阴影的结点为查找字母R时要检查的结点）：

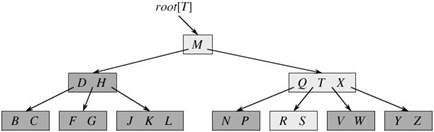
从上图轻易的看到，一个内结点x若含有n[x]个关键字，那么x将含有n[x]+1个子女；如含有2个关键字D H的内结点有3个子女，而含有3个关键字Q T X的内结点有4个子女。

2.1 用阶定义的B树

B 树又叫平衡多路查找树。一棵m阶的B 树 (注：切勿简单的认为一棵m阶的B树是m叉树，虽然存在四叉树，八叉树，KD树，及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树，但与B树完全不等同)的特性如下：

1. 树中每个结点最多含有m个孩子（m>=2）；
2. 除根结点和叶子结点外，其它每个结点至少有[ceil(m / 2)]个孩子（其中ceil(x)是一个取上限的函数）；
3. 若根结点不是叶子结点，则至少有2个孩子（特殊情况：没有孩子的根结点，即根结点为叶子结点，整棵树只有一个根节点）；
4. 所有叶子结点都出现在同一层，叶子结点没有孩子和指向孩子的指针，含有关键字信息(可以看做是外部结点或查询失败的结点，实际上这些结点不存在，指向这些结点的指针都为null)；
5. 每个非终端结点中包含有n个关键字信息： (n，P₀，K₁，P₁，K₂，P₂，......，K_n，P_n)。其中：
          a)   K_i (i=1...n)为关键字，且关键字按顺序升序排序K_i-1<
   K_i。

b)  
P_i为指向子树根的结点，且指针P_i-1指向子树中所有结点的关键字均小于K_i，但都大于K_i-1。

c)  
关键字的个数n必须满足： [ceil(m /
2)-1]<= n <= m-1。如下图所示：

B树中每一个结点能包含的关键字（如前面的D H和Q T X）数有一个上界和下界，这个下界可以用一个称作B树的最小度数（算法导论中文版上译为度数，最小度数即内结点中结点最小孩子数目）m（m>=2）表示。

2.2 用度定义的B树

l  每个非根的内结点至多有m个子女，每个非根的结点必须至少含有m-1个关键字，如果树是非空的，则根结点至少包含一个关键字；

l  每个结点可包含至多2m-1个关键字。所以一个内结点至多可有2m个子女。如果一个结点恰好有2m-1个关键字，我们就说这个结点是满的（B树要求至少半满）；

l  当关键字数m=2（t=2的意思是，m_min=2，m可以>=2）时的B树是最简单的（因此易误认为B树就是二叉查找树，但二叉查找树就是二叉查找树，B树就是B树，B树是一棵含有m（m>=2）个关键字的平衡多路查找树），此时，每个内结点可能因此而含有2个、3个或4个子女，亦即一棵2-3-4树，然而在实际中，通常采用大得多的t值。

B树中的每个结点根据实际情况可以包含大量的关键字信息和分支(当然不能超过磁盘块的大小，根据磁盘驱动(disk drives)的不同，一般块的大小在1k~4k左右)；这样树的深度降低了，这就意味着查找一个元素只要很少结点从外存磁盘中读入内存，很快访问到要查找的数据。

2.3 B树的类型和节点定义

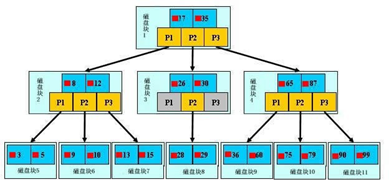
B树的类型和节点定义如下图所示：

2.4 文件查找的具体过程(涉及磁盘IO操作)

为了简单，用少量数据构造一棵3叉树的形式，实际应用中的B树结点中关键字很多。上面的图中比如根结点，其中17表示一个磁盘文件的文件名；小红方块表示这个17文件内容在硬盘中的存储位置；P1表示指向17左子树的指针。

其结构可以简单定义为：

typedef struct {

/*文件数*/

int  file_num;

/*文件名(key)  --- 17 */

char *
file_name[max_file_num];

/*指向子节点的指针 ---
P1…. */

BTNode * BTptr[max_file_num+1];

/*文件在硬盘中的存储位置 ---
小红方块 */

FILE_HARD_ADDR offset[max_file_num];

}BTNode;

假如每个盘块可以正好存放一个B树的结点（正好存放2个文件名）。那么一个BTNode结点就代表一个盘块，而子树指针就是存放另外一个盘块的地址。

模拟下查找文件29的过程：

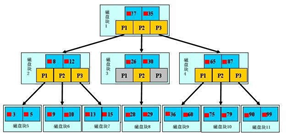
1. 根据根结点指针找到文件目录的根磁盘块1，将其中的信息导入内存。【磁盘IO操作 1次】
2. 此时内存中有两个文件名17、35和三个存储其他磁盘页面地址的数据。根据算法我们发现：17<29<35，因此我们找到指针p2。
3. 根据p2指针，我们定位到磁盘块3，并将其中的信息导入内存。【磁盘IO操作 2次】
4. 此时内存中有两个文件名26，30和三个存储其他磁盘页面地址的数据。根据算法我们发现：26<29<30，因此我们找到指针p2。
5. 根据p2指针，我们定位到磁盘块8，并将其中的信息导入内存。【磁盘IO操作 3次】
6. 此时内存中有两个文件名28，29。根据算法我们查找到文件名29，并定位了该文件内存的磁盘地址。

分析上面的过程，发现需要3次磁盘IO操作和3次内存查找操作，关于内存中的文件名查找，由于是一个有序表结构，可以利用折半查找提高效率，至于IO操作是影响整个B树查找效率的决定因素。

当然，如果使用平衡二叉树的磁盘存储结构来进行查找，磁盘4次，最多5次，而且文件越多，B树比平衡二叉树所用的磁盘IO操作次数将越少，效率也越高。

2.5 B树的高度

根据上面的例子可以看出，对于辅存做IO读的次数取决于B树的高度，而B树的高度由什么决定的呢？

若B树某一非叶子结点包含N个关键字，则此非叶子结点含有N+1个孩子结点，而所有的叶子结点都在第I层，可以得出：

1. 因为根至少有两个孩子，因此第2层至少有两个结点。
2. 除根和叶子外，其它结点至少有┌m/2┐个孩子，
3. 因此在第3层至少有2*┌m/2┐个结点，
4. 在第4层至少有2*(┌m/2┐^2)个结点，
5. 在第 I 层至少有2*(┌m/2┐^(l-2)
   )个结点，于是有：N+1 ≥ 2*┌m/2┐I-2；
6. 考虑第L层的结点个数为N+1，那么2*(┌m/2┐^(l-2)）≤N+1，也就是L层的最少结点数刚好达到N+1个，即：
   I≤ log┌m/2┐((N+1)/2 )+2；

　所以

• 当B树包含N个关键字时，B树的最大高度为l-1（因为计算B树高度时，叶结点所在层不计算在内），即：I - 1
  = log┌m/2┐((N+1)/2 )+1。

　这个B树的高度公式从侧面显示了B树的查找效率是相当高的。

问题：一棵含有N个总关键字数的m阶的B树的最大高度是多少?

答：log_ceil（m/2）(N+1)/2 + 1 （上面中关于m阶B树的第1点特性已经提到：树中每个结点含有最多含有m个孩子，即m满足：ceil(m/2)<=m<=m。而树中每个结点含孩子数越少，树的高度则越大，故如此）。