[BUAA_SE_2017]个人项目-Sudoku

个人项目作业-数独

Github项目地址

时间预估

PSP2.1	Personal Software Process Stages	预估时间（分钟）	实际耗时（分钟）
Planning	计划	60
· Estimate	· 估计这个任务需要多少时间	60
Development	开发	1350
· Analysis	· 需求分析 (包括学习新技术)	180
· Design Spec	· 生成设计文档	180
· Design Review	· 设计复审 (和同事审核设计文档)	60
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30
· Design	· 具体设计	180
· Coding	· 具体编码	300
· Code Review	· 代码复审	120
· Test	· 测试（自我测试，修改代码，提交修改）	300
Reporting	报告	260
· Test Report	· 测试报告	120
· Size Measurement	· 计算工作量	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	120
	合计	1670

解题思路

• 生成数独终局：

  • 首先生成左上角第一个3x3正方形，其中左上角格为LEFTTOP，共可生成8!=40320种组合；
  • 每一种组合都可通过(1x3或3x1的单元)排列组合扩散得到一个数独终局，记作该组合下基础数独终局；
  • 某一组合下的基础数独终局可通过分别交换456列三列、789列三列、456行三行、789行三行得到正确衍生数独终局；根据排列组合原理，任一组合下的数独终局可生成衍生数独终局(3!)^4=1296个，且不重复；

• 求解数独：

  • 回溯法求解，当且仅当当前格赋值使得其它未填格无值可取时，更换当前格值；
  • 若数独有解，则一定能找到；

实现过程

• 生成数独终局：

  • 左上第一个3x3方格除第一个元素（左上角）外，利用遍历全排列得到基础数块；
  • 再根据该基础数块扩散得到基础数独；
  • 分别利用456列三列、789列三列、456行三行、789行三行的全排列，替换相应行列，得到合法数独终局。

• 求解数独：

  • 从（1，1）至（81，81）遍历，将每一次赋值压入栈中；
  • 遇某格无数可填时，弹出栈顶元素，更换取值，遍历位置回到栈顶元素，直至有值可取；
  • 因此，若数独有解，则遍历结束时，所有未完成格均合法，即找到一解。

• 类：

  • 程序除主类外共有6个类，其中输入、输出处理模块两个类，数独结构存储三个类，计算功能一个类；
  • InputHandler类识别输入有效性，提取输入信息；
  • SudokuNode类表示每一个数独格子结点，有自身取值、所在行、列、格的指针；
  • SudokuUnit类代表行或列或格，存储各数字存在情况；
  • SudokuHead类封装9x9个SudokuNode，代表一个结构完整的数独；
  • Calculator类实现了生成、求解数独的方法；
  • OutputHandler类利用静态方法实现了数独的快速输出。

• 单元测试设计：

  • 单元测试设计针对如下方面：
    • 非法参数
    • 数独存储结构检验
    • 基础数独的生成检验
    • 求解数独的顺序检验
  • 如下图，单元测试均通过。

优化改进

• 生成数独：

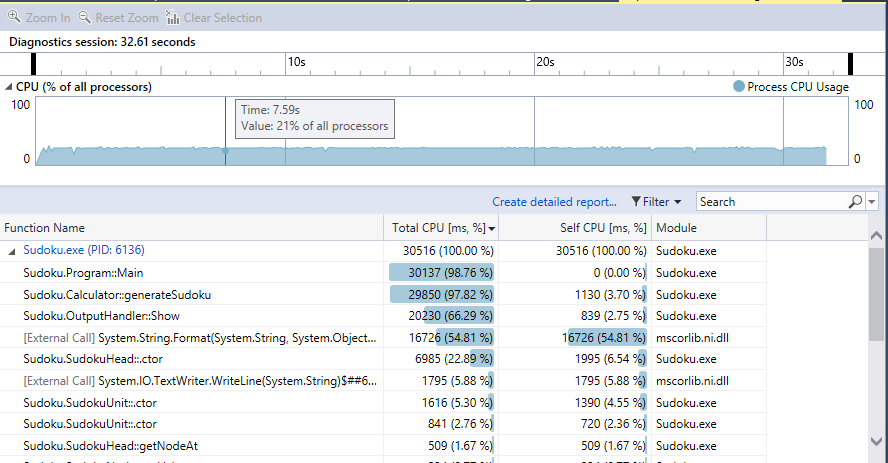
  • 第一版生成1百万需要32.67秒，最终版需要7.15秒；
  • 优化手段：该方法生成的耗时本身不长，重点在于输出时对文件写入，以及整形转换为字符串的耗时。

  优化前：

  public static int Show(int[][] matrix)
      {
          for (int i = 0; i < 9; i++)
          {
              for(int j = 0; j < 9; j++)
              {
                  sw.write((matrix[i][j]);
                  sw.write(" ");
              }
              sw.write("\n");
          }
          sw.Write("\n");
  		sw.Flush();
          return 0;
      }
  

优化后：
```
public static int Show(int[][] matrix)
    {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < 9; i++)
        {
            for(int j = 0; j < 9; j++)
            {
                sb.Append((char)(matrix[i][j] + 48));
                sb.Append(' ');
            }
            sb.AppendLine();
        }
        sw.WriteLine(sb.ToString());
        return 0;
    }
```

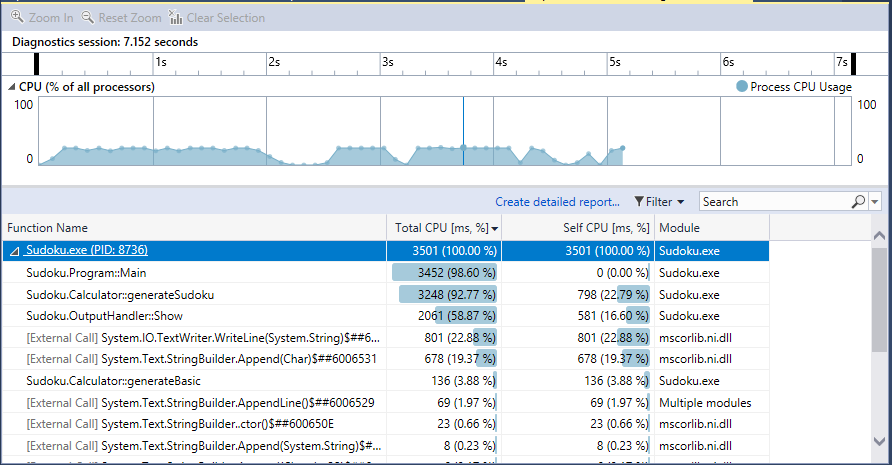
**另外一点，StreamWriter的flush()耗时较长，因此优化后设置每10000个数独flush()一次，此时flush()耗时忽略不计；其次，10000个数独对于缓冲区来说不会溢出，但缓冲区存在上限，因此应及时将其清空。**

• 求解数独：
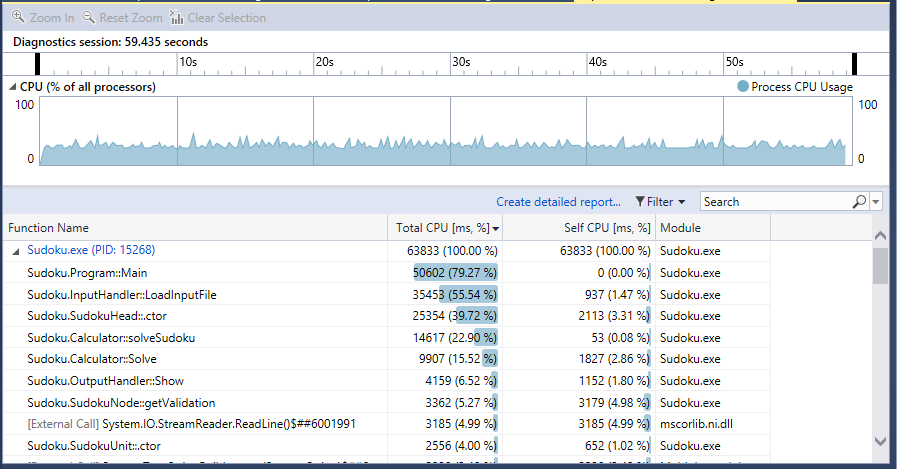
  • 第一版生成1百万需要5分钟...，最终版需要59秒（好不容易压进一分钟，测试数据应该属于不是那么难得数独）
  • 优化手段：削减复杂度，减少建立存储结构时的时间浪费。利用StringBuilder处理读如的一行文本信息；部分类成员变量作用域修饰符用public取代private，以空间换时间；构造SudokuHead时，减少时间复杂度；

**因改动比较细小，在此不列出代码**

关键代码

• 生成数独关键代码部分：生成全排列
  
  利用离散数学中讲到的箭头生成排列方法生成，因为其每一次生成取决于上一次生成结果，因此适合用于此。

        public int generateBasic(int[] prev, bool[] arrow)
        {
            if(prev[0] == 0)
            {
                for (int i = 0; i < prev.Length; i++)
                {
                    prev[i] = i + 1;
                    arrow[i] = false;
                }
                return 0;
            }
            else
            {
                int max = -1;
                int index = -1;
                for(int i = 0; i < prev.Length; i++)
                {
                    if(arrow[i] && i == prev.Length - 1 || !arrow[i] && i == 0)
                    {
                        continue;
                    }
                    int compare = arrow[i] ? prev[i+1] : prev[i-1];
                    if(compare < prev[i])
                    {
                        if(prev[i] > max)
                        {
                            max = prev[i];
                            index = i;
                        }
                    }
                }
                if(max == -1)
                {
                    return -1;
                }
                int tmp = prev[index];
                prev[index] = arrow[index] ? prev[index + 1] : prev[index - 1];
                prev[index + (arrow[index] ? 1 : -1)] = tmp;
                for(int i = 0; i < prev.Length; i++)
                {
                    if(prev[i] > tmp)
                    {
                        arrow[i] = !arrow[i];
                    }
                }
                return 0;
            }
        }

• 求解数独关键代码：回溯、出入栈
  
  利用C#中Collections中的Stack类做栈操作

public int Solve(SudokuNode[][] nodes, Stack operationStack)
        {
            int count = 0;
            for(int i = 0; i < 9; i++)
            {
                for(int j = 0; j < 9; j++)
                {
                    if(!nodes[i][j].getFlag() && nodes[i][j].getValue() != 0)
                    {
                        count++;
                    }
                    else
                    {
                        SudokuNode node = nodes[i][j];
                        bool[] validation = new bool[9];
                        if (node.getValidation(validation))
                        {
                            node.setValue(node.nextValue());
                            operationStack.Push(node);
                        }
                        else
                        {
                            node.reset();
                            SudokuNode prev = (SudokuNode)(operationStack.Pop());
                            i = prev.x;
                            j = prev.y - 1;
                            prev.Flag();
                        }
                    }
                }
            }
            return 0;
        }

实际耗时

PSP2.1	Personal Software Process Stages	预估时间（分钟）	实际耗时（分钟）
Planning	计划	60	30
· Estimate	· 估计这个任务需要多少时间	60	30
Development	开发	1350	1180
· Analysis	· 需求分析 (包括学习新技术)	180	150
· Design Spec	· 生成设计文档	180	90
· Design Review	· 设计复审 (和同事审核设计文档)	60	10
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	30	0
· Design	· 具体设计	180	240
· Coding	· 具体编码	300	360
· Code Review	· 代码复审	120	30
· Test	· 测试（自我测试，修改代码，提交修改）	300	300
Reporting	报告	260	65
· Test Report	· 测试报告	120	30
· Size Measurement	· 计算工作量	20	5
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	120	30
	合计	1670	1275

总结

本次个人项目作业我花了非常多的时间在研究怎么优化IO上，虽然最后的成果是大幅减小了我的程序运行时间，但是和其他同学以及巨佬比起来还是太naive了，而且求解数独的算法上使用的是复杂度很高的回溯法。因此，通过这次个人项目作业，最大的收获在于认识到了自身极大的不足，继续好好学习去。。

在PSP2.1上，认为要在coding前先全部设计好，定好代码规范，然而实际上并没有认认真真好好设计。回过头看，如果在设计阶段做好了调研以及好的优化想法，那么到后来的优化会显得非常容易。因此，下次项目coding前一定做足准备工作。（更多关于这方面想say的，就放在week1另外一个作业里吧）

---

数独附加题Github项目地址

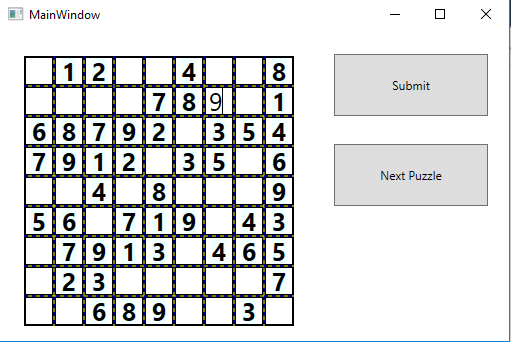
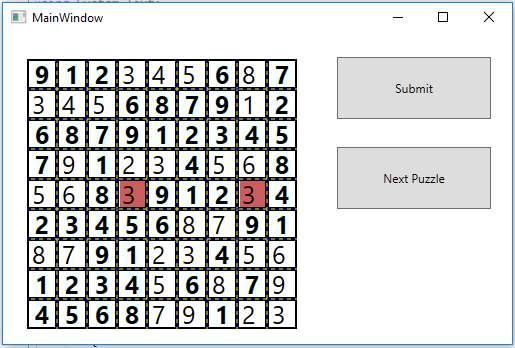
简单制作了一个GUI界面，支持数独题生成并显示，用户可在上进行输入，并检查答案是否正确。（不需要什么依赖包，C#wpf桌面应用）