pta 编程题10 Root of AVL Tree

其它pta数据结构编程题请参见：pta

这道题考察平衡二叉查找树的插入。

为了保证二叉查找树的平衡，当一个结点的左右子树的高度差大于1时就要进行调整。

分为以下四种情况：

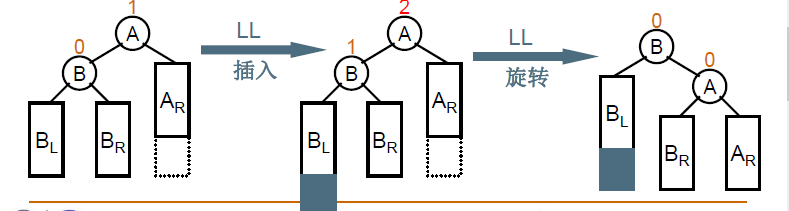
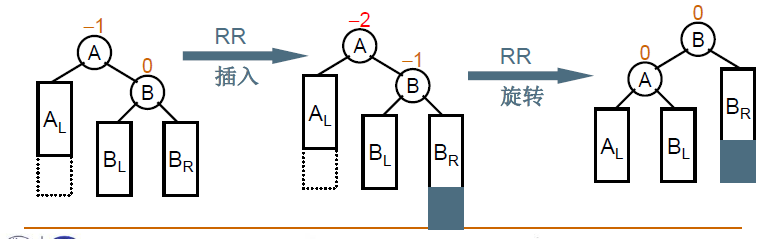
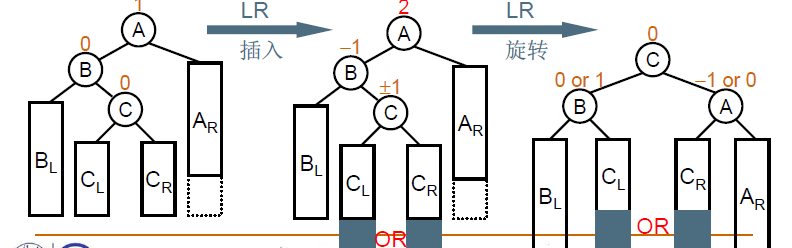
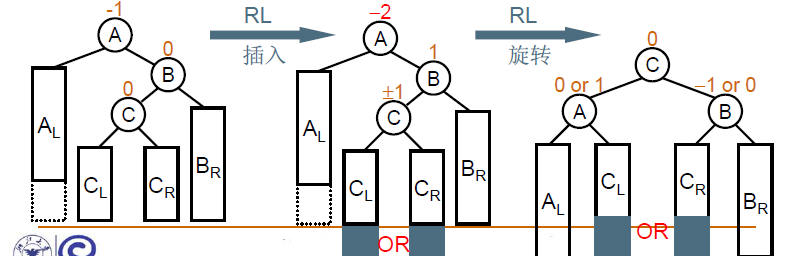
插入新节点后，以及旋转之后，需要更新结点的高度。

RL旋转可以通过右孩子的LL旋转，然后当前节点的RR旋转实现。

同理，LR旋转可以通过左孩子的RR旋转，然后当前节点的LL旋转实现。

 #include <iostream>
 using namespace std;

 typedef struct Node *Tree;
 struct Node
 {
     int data;
     Tree left;
     Tree right;
     int height;
 };

 Tree insert(Tree T, int X);
 Tree ll(Tree A);
 Tree lr(Tree A);
 Tree rr(Tree A);
 Tree rl(Tree A);
 int getHeight(Tree T);
 int max(int a, int b);
 Tree createNode(int X);

 int main()
 {
     int N, X, i;
     cin >> N >> X;
     Tree root = createNode(X);
     for (i = ; i < N; i++)
     {
         cin >> X;
         root = insert(root, X);
     }
     cout << root->data;
     return ;
 }

 Tree insert(Tree T, int X)
 {
     if (!T)
         T = createNode(X);
     else if (X < T->data)
     {
         T->left = insert(T->left, X);
         if (getHeight(T->left) - getHeight(T->right) == )
         {
             if (X < T->left->data)
                 T = ll(T);
             else
                 T = lr(T);
         }
     }
     else if (X > T->data)
     {
         T->right = insert(T->right, X);
         if (getHeight(T->right) - getHeight(T->left) == )
         {
             if (X > T->right->data)
                 T = rr(T);
             else
                 T = rl(T);
         }
     }
     T->height = max(getHeight(T->left), getHeight(T->right)) + ;
     return T;
 }

 Tree ll(Tree A)
 {
     Tree B = A->left;
     A->left = B->right;
     B->right = A;
     A->height = max(getHeight(A->left), getHeight(A->right)) + ;
     B->height = max(getHeight(A->left), A->height) + ;
     return B;
 }

 Tree rr(Tree A)
 {
     Tree B = A->right;
     A->right = B->left;
     B->left = A;
     A->height = max(getHeight(A->left), getHeight(A->right)) + ;
     B->height = max(A->height, getHeight(B->right)) + ;
     return B;
 }

 Tree lr(Tree A)
 {
     A->left = rr(A->left);
     return ll(A);
 }

 Tree rl(Tree A)
 {
     A->right = ll(A->right);
     return rr(A);
 }

 int getHeight(Tree T)
 {
     if (T == NULL) return ;
     else return T->height;
 }

 int max(int a, int b)
 {
     return a > b ? a : b;
 }

 Tree createNode(int X)
 {
     Tree T;
     T = new Node;
     T->data = X;
     T->left = T->right = NULL;
     T->height = ;
     return T;
 }