选课 ( dp 树形dp 动态规划 树规)

和某篇随笔重了？！！？！？！？！？！？不管了留着吧

题目：

在大学里每个学生，为了达到一定的学分，必须从很多课程里选择一些课程来学习，在课程里有些课程必须在某些课程之前学习，如高等数学总是在其它课程之前学习。现在有N门功课，每门课有个学分，每门课有一门或没有直接先修课（若课程a是课程b的先修课即只有学完了课程a，才能学习课程b）。一个学生要从这些课程里选择M门课程学习，问他能获得的最大学分是多少？

输入

第一行有两个整数N,M用空格隔开。(1<=N<=200,1<=M<=150)
接下来的N行,第I+1行包含两个整数ki和si, ki表示第I门课的直接先修课，si表示第I门课的学分。若ki=0表示没有直接先修课（1<=ki<=N, 1<=si<=20）。

输出

只有一行，选M门课程的最大得分。

样例输入

7  4
2  2
0  1
0  4
2  1
7  1
7  6
2  2

样例输出

13

题解

多叉树转二叉树。树形dp。

1.多叉树转二叉树转法：

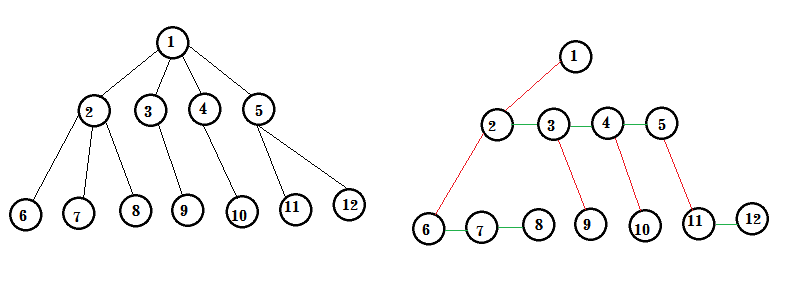
我们用到的是孩子兄弟法。

对于每一个节点，他在二叉树中的左孩子是在多叉树中的第一个孩子，他在二叉树中的右孩子是在多叉树中的第一个兄弟。

如上图，左边的是原来的多叉树，右边的是二叉树，其中红色线表示左孩子的关系，绿色线表示右孩子的关系。

比如节点2，在多叉树中的第一个孩子是6，那么他在二叉树中的左孩子是6。第一个兄弟是3，所以在二叉树中的右孩子是3。

为什么我们要转换呢？因为方便记忆化搜索处理状态啊！

因为输入的是一个森林，我们就通过节点0来代表一棵树的根的父亲(这是很方便的，因为输入数据就是这样的:若ki=0表示没有直接先修课)。

------------------------------------------------------------------

2.然后是树形dp。我这里用的记忆化搜索。

dfs(i,j)代表当前要考虑第i个课程及以其为根的二叉树中的子树的选择情况，j表示当前能够选择多少门课程。

根据题意可知,现在正在考虑第i门课程的情况时，必须已经选择了第i门课程在多叉树中的爹(要不选个毛啊)。所以我们可以直接略过第i门课程，去考虑第i门课程的右孩子(多叉树中的下一个兄弟)，当然也不能考虑自己的左孩子(多叉树中的孩子)了。

我们还需要选第i门课程的情况。选第i门课程，就得加上这门课程的学分，然后剩余总课程--。剩下的课程可以分给自己的左孩子(多叉树中的孩子)一些，剩下的分给自己的右孩子(多叉树中的兄弟)。在dfs中，for(int k=0;k<j;k++)这里面的这个k就是给左孩子多少。那么就更新答案为。自己的学分+dfs左孩子的学分+dfs右孩子的学分。

简洁的main函数就是读入->转换->dfs并输出答案。这里我们不dfs 0，而是直接dfs 0的左孩子(之前说过0是整个森林的根)，是因为防止在边界判断时候把0判断掉。

3.代码

#include <iostream>
using namespace std;
int n,m;
int a[2001],f[2001];//a[i]是某一门课程的学分 f[i]是某一门课程在多叉树中的爹
int lChild[2001],rChild[2001];//二叉树的左子树和柚子树
int dp[2001][2001];//dp[i][j]是以第i个节点为根的二叉树（注意是二叉树），能选择j门课程时候的最大学分。
void convert()//多叉树 -> 二叉树
{
        for(int i=1;i<=n;i++)//遍历每一个节点
        {
                int fa=f[i];//这个节点的爹
                if(lChild[fa]==0)lChild[fa]=i;//这个节点的爹还没有孩子，所以这个节点就是这个节点的爹的第一个孩子
                else//这个节点的爹有孩子，所以这个节点在二叉树中就应该是这个节点的爹的左孩子的最右边的叶子的孩子
                {
                        fa=lChild[fa];//暂时让变量fa变成爹的第一个孩子(二叉树中的左孩子)
                        while(rChild[fa])fa=rChild[fa];//循环找最右边的叶子
                            rChild[fa]=i;//成为最右边的叶子的右孩子
                }
        }
}
int dfs(int i,int j)//i是当前节点的编号，j是当前可以选择的课程数目
{
        if(i<1||j<1||i>n||j>m)return 0;//边界判断
        if(dp[i][j]!=0)return dp[i][j];//查备忘录
        for(int k=0;k<j;k++)//选给左子树k个，自己留一个（得选自己，否则无法选左孩子），剩下的给右
                dp[i][j]=max(dp[i][j],a[i]+dfs(lChild[i],k)+dfs(rChild[i],j-k-1));//自己的学分+dfs左孩子的学分+dfs右孩子的学分
        dp[i][j]=max(dp[i][j],dfs(rChild[i],j));//略过自己，都给右孩子
        return dp[i][j];//最后返回答案
}

int main()
{
        cin >> n >> m;
        for(int i=1;i<=n;i++)
                cin >> f[i] >> a[i];
        convert();
        cout << dfs(lChild[0],m) << endl;
        return 0;
}