DLX精确覆盖与重复覆盖模板题

hihoCoder #1317 : 搜索四·跳舞链

原题地址：http://hihocoder.com/problemset/problem/1317

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Ho最近遇到一个难题，他需要破解一个棋局。

棋局分成了n行，m列，每行有若干个棋子。小Ho需要从中选择若干行使得每一列有且恰好只有一个棋子。

比如下面这样局面：

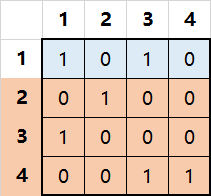
其中1表示放置有棋子的格子，0表示没有放置棋子。

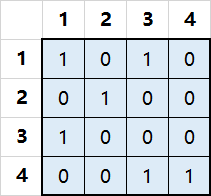
对于上面这个问题，小Ho经过多次尝试以后得到了解为选择2、3、4行就可以做到。

但是小Ho觉得自己的方法不是太好，于是他求助于小Hi。

小Hi：小Ho你是怎么做的呢？

小Ho：我想每一行都只有两种状态，选中和未被选中。那么我将选中视为1，未选中视为0。则每一种组合恰好对应了一个4位的01串，也就是一个4位的二进制数。

小Hi：恩，没错。

小Ho：然后我所做的就是去枚举每一个二进制数然后再来判定是否满足条件。

小Hi：小Ho你这个做法本身没什么问题，但是对于棋盘行数再多一点的情况就不行了。

小Ho：恩，我也这么觉得，那你有什么好方法么？

小Hi：我当然有了，你听我慢慢道来。

提示：跳舞链

输入

第1行：1个正整数t，表示数据组数，1≤t≤10。

接下来t组数据，每组的格式为：

第1行：2个正整数n,m，表示输入数据的行数和列数。2≤n,m≤100。

第2..n+1行：每行m个数，只会出现0或1。

输出

第1..t行：第i行表示第i组数据是否存在解，若存在输出"Yes"，否则输出"No"。

样例输入

2

4 4

1 1 0 1

0 1 1 0

1 0 0 0

0 1 0 1

4 4

1 0 1 0

0 1 0 0

1 0 0 0

0 0 1 1

样例输出

No

Yes

DLX精确覆盖

#include <algorithm>
#include <cstring>
#include <string.h>
#include <iostream>
#include <list>
#include <map>
#include <set>
#include <stack>
#include <string>
#include <utility>
#include <queue>
#include <vector>
#include <cstdio>
#include <cmath>

#define LL long long

using namespace std;

const int maxnode = ; //最多多少个‘1’
const int MaxM = ;
const int MaxN = ;

struct DLX
{
    int n,m,SIZE;
    int U[maxnode],D[maxnode],R[maxnode],L[maxnode],Row[maxnode],Col[maxnode];//L,R,D,U四个数组记录某节点上下左右邻居
    int H[MaxN], S[MaxM];//H记录排头，S记录某列有多少个节点
    int ansd, ans[MaxN];
    void init(int _n,int _m)
    {
        n = _n;
        m = _m;
        for(int i = ;i <= m;i++)
        {
            S[i] = ;
            U[i] = D[i] = i;
            L[i] = i-;
            R[i] = i+;
        }
        R[m] = ; L[] = m;
        SIZE = m;
        for(int i = ;i <= n;i++)
            H[i] = -;
    }
    void Link(int r,int c)
    {
        ++S[Col[++SIZE]=c];
        Row[SIZE] = r;
        D[SIZE] = D[c];
        U[D[c]] = SIZE;
        U[SIZE] = c;
        D[c] = SIZE;
        if(H[r] < )H[r] = L[SIZE] = R[SIZE] = SIZE;
        else
        {
            R[SIZE] = R[H[r]];
            L[R[H[r]]] = SIZE;
            L[SIZE] = H[r];
            R[H[r]] = SIZE;
        }
    }
    void exact_Remove(int c)
    {
        L[R[c]] = L[c]; R[L[c]] = R[c];
        for(int i = D[c];i != c;i = D[i])
            for(int j = R[i];j != i;j = R[j])
            {
                U[D[j]] = U[j];
                D[U[j]] = D[j];
                --S[Col[j]];
            }
    }
    void repeat_remove(int c) {
    for(int i = D[c]; i != c; i = D[i])
        L[R[i]] = L[i], R[L[i]] = R[i];
    }
    void repeat_resume(int c) {
    for(int i = U[c]; i != c; i = U[i])
        L[R[i]] = R[L[i]] = i;
    }

    int f() { //估价函数。
    bool vv[MaxM];
    int ret = , c, i, j;
    for(c = R[]; c != ; c = R[c]) vv[c] = ;
    for(c = R[]; c != ; c = R[c])
        if(vv[c]) {
            ++ret, vv[c] = ;
            for(i = D[c]; i != c; i = D[i])
                for(j = R[i]; j != i; j = R[j])
                    vv[Col[j]] = ;
        }
    return ret;
    }

    void repeat_dance(int d) {
    if(d + f() >= ansd) return; //估价函数剪枝，A*搜索
    if(R[] == ) {
        if(d < ansd) ansd = d;
        return;
    }
    int c = R[], i, j;
    for(i = R[]; i; i = R[i])
        if(S[i] < S[c]) c = i;
    for(i = D[c]; i != c; i = D[i]) {
        repeat_remove(i);
        for(j = R[i]; j != i; j = R[j]) repeat_remove(j);
        repeat_dance(d + );
        for(j = L[i]; j != i; j = L[j]) repeat_resume(j);
        repeat_resume(i);
    }
}
    void exact_resume(int c)
    {
        for(int i = U[c];i != c;i = U[i])
            for(int j = L[i];j != i;j = L[j])
                ++S[Col[U[D[j]]=D[U[j]]=j]];
        L[R[c]] = R[L[c]] = c;
    }
    //d为递归深度
    bool exact_Dance(int d)
    {
        if(R[] == )
        {
            ansd = d;
            return true;
        }
        int c = R[];
        for(int i = R[];i != ;i = R[i])
            if(S[i] < S[c])
                c = i;
        exact_Remove(c);
        for(int i = D[c];i != c;i = D[i])
        {
            ans[d] = Row[i];
            for(int j = R[i]; j != i;j = R[j]) exact_Remove(Col[j]);
            if(exact_Dance(d+))return true;
            for(int j = L[i]; j != i;j = L[j]) exact_resume(Col[j]);
        }
        exact_resume(c);
        return false;
    }
};

DLX g;
int main()
{
    int n,m;
    int t;
    cin>>t;

    while( t--)
    {
        scanf("%d%d",&n,&m);
        g.init(n,m);
        for(int i = ;i <= n;i++)
        {
            int num;
            for(int j=;j<=m;j++)
                {
                    scanf("%d",&num);
                    if(num==) g.Link(i,j);
                }
        }
        if(!g.exact_Dance())printf("No\n");
        else
            printf("Yes\n");
    }
    return ;
}

HDU 3498 whosyourdaddy

http://acm.hdu.edu.cn/showproblem.php?pid=3498

whosyourdaddy

Time Limit: 20000/10000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 1686    Accepted Submission(s): 841

Problem
Description

sevenzero
liked Warcraft very much, but he haven't practiced it for several years after
being addicted to algorithms. Now, though he is playing with computer, he
nearly losed and only his hero Pit Lord left. sevenzero is angry, he decided
to cheat to turn defeat into victory. So he entered "whosyourdaddy",
that let Pit Lord kill any hostile unit he damages immediately. As all
Warcrafters know, Pit Lord masters a skill called Cleaving Attack and he can
damage neighbour units of the unit he attacks. Pit Lord can choice a position
to attack to avoid killing partial neighbour units sevenzero don't want to
kill. Because sevenzero wants to win as soon as possible, he needs to know
the minimum attack times to eliminate all the enemys.

Input

There
are several cases. For each case, first line contains two integer N (2 ≤ N ≤
55) and M (0 ≤ M ≤ N*N),and N is the number of hostile units. Hostile units
are numbered from 1 to N. For the subsequent M lines, each line contains two
integers A and B, that means A and B are neighbor. Each unit has no more than
4 neighbor units. The input is terminated by EOF.

Output

One
line shows the minimum attack times for each case.

Sample
Input

5 4

1 2

1 3

2 4

4 5

6 4

1 2

1 3

1 4

4 5

Sample Output

2

3

Author

sevenzero

Source

2010 ACM-ICPC Multi-University Training Contest（7）——Host by HIT

DLX重复覆盖

n个敌对单元，m对单元互相相邻，建图的邻接矩阵，DLX。

#include <algorithm>
#include <cstring>
#include <string.h>
#include <iostream>
#include <list>
#include <map>
#include <set>
#include <stack>
#include <string>
#include <utility>
#include <queue>
#include <vector>
#include <cstdio>
#include <cmath>

#define LL long long

using namespace std;

const int maxnode = ; //最多多少个1
const int MaxM = ;
const int MaxN = ;

struct DLX
{
    int n,m,SIZE;
    int U[maxnode],D[maxnode],R[maxnode],L[maxnode],Row[maxnode],Col[maxnode];//L,R,D,U四个数组记录某节点上下左右邻居
    int H[MaxN], S[MaxM];//H记录行头，S记录某列有多少个节点
    int ansd, ans[MaxN];
    void init(int _n,int _m)
    {
        n = _n;
        m = _m;
        for(int i = ;i <= m;i++)
        {
            S[i] = ;
            U[i] = D[i] = i;
            L[i] = i-;
            R[i] = i+;
        }
        R[m] = ; L[] = m;
        SIZE = m;
        for(int i = ;i <= n;i++)
            H[i] = -;
    }
    void Link(int r,int c)
    {
        ++S[Col[++SIZE]=c];
        Row[SIZE] = r;
        D[SIZE] = D[c];
        U[D[c]] = SIZE;
        U[SIZE] = c;
        D[c] = SIZE;
        if(H[r] < )H[r] = L[SIZE] = R[SIZE] = SIZE;
        else
        {
            R[SIZE] = R[H[r]];
            L[R[H[r]]] = SIZE;
            L[SIZE] = H[r];
            R[H[r]] = SIZE;
        }
    }
    void exact_Remove(int c)
    {
        L[R[c]] = L[c]; R[L[c]] = R[c];
        for(int i = D[c];i != c;i = D[i])
            for(int j = R[i];j != i;j = R[j])
            {
                U[D[j]] = U[j];
                D[U[j]] = D[j];
                --S[Col[j]];
            }
    }
    void repeat_remove(int c) {
    for(int i = D[c]; i != c; i = D[i])
        L[R[i]] = L[i], R[L[i]] = R[i];
    }
    void repeat_resume(int c) {
    for(int i = U[c]; i != c; i = U[i])
        L[R[i]] = R[L[i]] = i;
    }

    int f() { //估价函数。
    bool vv[MaxM];
    int ret = , c, i, j;
    for(c = R[]; c != ; c = R[c]) vv[c] = ;
    for(c = R[]; c != ; c = R[c])
        if(vv[c]) {
            ++ret, vv[c] = ;
            for(i = D[c]; i != c; i = D[i])
                for(j = R[i]; j != i; j = R[j])
                    vv[Col[j]] = ;
        }
    return ret;
    }

    void repeat_dance(int d) {
    if(d + f() >= ansd) return; //估价函数剪枝，A*搜索
    if(R[] == ) {
        if(d < ansd) ansd = d;
        return;
    }
    int c = R[], i, j;
    for(i = R[]; i; i = R[i])
        if(S[i] < S[c]) c = i;
    for(i = D[c]; i != c; i = D[i]) {
        repeat_remove(i);
        for(j = R[i]; j != i; j = R[j]) repeat_remove(j);
        repeat_dance(d + );
        for(j = L[i]; j != i; j = L[j]) repeat_resume(j);
        repeat_resume(i);
    }
}
    void exact_resume(int c)
    {
        for(int i = U[c];i != c;i = U[i])
            for(int j = L[i];j != i;j = L[j])
                ++S[Col[U[D[j]]=D[U[j]]=j]];
        L[R[c]] = R[L[c]] = c;
    }
    //d为递归深度
    bool exact_Dance(int d)
    {
        if(R[] == )
        {
            ansd = d;
            return true;
        }
        int c = R[];
        for(int i = R[];i != ;i = R[i])
            if(S[i] < S[c])
                c = i;
        exact_Remove(c);
        for(int i = D[c];i != c;i = D[i])
        {
            ans[d] = Row[i];
            for(int j = R[i]; j != i;j = R[j]) exact_Remove(Col[j]);
            if(exact_Dance(d+))return true;
            for(int j = L[i]; j != i;j = L[j]) exact_resume(Col[j]);
        }
        exact_resume(c);
        return false;
    }
};

DLX dlx;
int main()
{
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        dlx.init(n,n);
        while(m--)
        {
            int a,b;
            scanf("%d%d",&a,&b);
            dlx.Link(a,b);
            dlx.Link(b,a);
        }
        for(int i=;i<=n;i++)dlx.Link(i,i);
        dlx.ansd=0x3f3f3f;
        dlx.repeat_dance();
        printf("%d\n",dlx.ansd);
    }
    return ;
}