BZOJ3033 太鼓达人

3033: 太鼓达人

Time Limit: 1 Sec  Memory Limit: 128 MB
Submit: 690  Solved: 497
[Submit][Status][Discuss]

Description

　　七夕祭上，Vani牵着cl的手，在明亮的灯光和欢乐的气氛中愉快地穿行。这时，在前面忽然出现了一台太鼓达人机台，而在机台前坐着的是刚刚被精英队伍成员XLk、Poet_shy和lydrainbowcat拯救出来的的applepi。看到两人对太鼓达人产生了兴趣，applepi果断闪人，于是cl拿起鼓棒准备挑战。然而即使是在普通难度下，cl的路人本性也充分地暴露了出来。一曲终了，不但没有过关，就连鼓都不灵了。Vani十分过意不去，决定帮助工作人员修鼓。

　　鼓的主要元件是M个围成一圈的传感器。每个传感器都有开和关两种工作状态，分别用1和0表示。显然，从不同的位置出发沿顺时针方向连续检查K个传感器可以得到M个长度为K的01串。Vani知道这M个01串应该是互不相同的。而且鼓的设计很精密，M会取到可能的最大值。现在Vani已经了解到了K的值，他希望你求出M的值，并给出字典序最小的传感器排布方案。

Input

　　一个整数K。

　

Output

　一个整数M和一个二进制串，由一个空格分隔。表示可能的最大的M，以及字典序最小的排布方案，字符0表示关，1表示开。你输出的串的第一个字和最后一个字是相邻的。

Sample Input

3

Sample Output

8 00010111

HINT

　得到的8个01串分别是000、001、010、101、011、111、110和100。注意前后是相邻的。长度为3的二进制串总共只有8种，所以M = 8一定是可能的最大值。

　　对于全部测试点，2≤K≤11。

Source

Poetize2

[Submit][Status][Discuss]

HOME
Back

---

题解

参照Clove_unique的题解

这道题实际上是将k-1位的二进制数看做点，k位的二进制数看成边，并且连接两个点的边就是将这两个点的权像这样联系起来



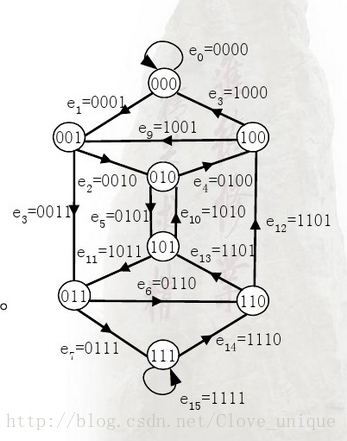
然后每个点的入度和出度相等并且全部是偶点，是一个标准的欧拉图，所以只需要在这个图中找字典序最小的欧拉回路就行了

可以贪心地找字典序较小的边，然后实在不行了就回溯

这样的话时间复杂度是接近O(n+m)的

#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
    rg T data=0,w=1;rg char ch=getchar();
    for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
    for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
    return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;

co int N=2048;
int p[20],n,t;
bool v[N],ans[N];
bool dfs(int x,int k){
	if(v[x]) return 0;
	if(k==t) return 1;
	ans[k]=x&1;
	v[x]=1;
	if(dfs((x<<1)&(t-1),k+1)) return 1;
	if(dfs((x<<1|1)&(t-1),k+1)) return 1;
	v[x]=0;
	return 0;
}
int main(){
	p[0]=1;
	for(int i=1;i<20;++i) p[i]=p[i-1]<<1;
	read(n);
	printf("%d ",t=p[n]);
	dfs(0,1);
	for(int i=1;i<n;++i) putchar('0');
	for(int i=1;i<=t-n+1;++i) printf("%d",ans[i]);
	puts("");
	return 0;
}