【Gradient Boosted Decision Tree】林轩田机器学习技术

GBDT之前实习的时候就听说应用很广，现在终于有机会系统的了解一下。

首先对比上节课讲的Random Forest模型，引出AdaBoost-DTree(D)

AdaBoost-DTree可以类比AdaBoost-Stump模型，就可以直观理解了

1）每轮都给调整sample的权重

2）获得gt(D,ut)

3）计算gt的投票力度alphat

最后返回一系列gt的线性组合。

weighted error这个比较难搞，有没有不用动原来的模型，通过输入数据上做文章就可以达到同样的目的呢?

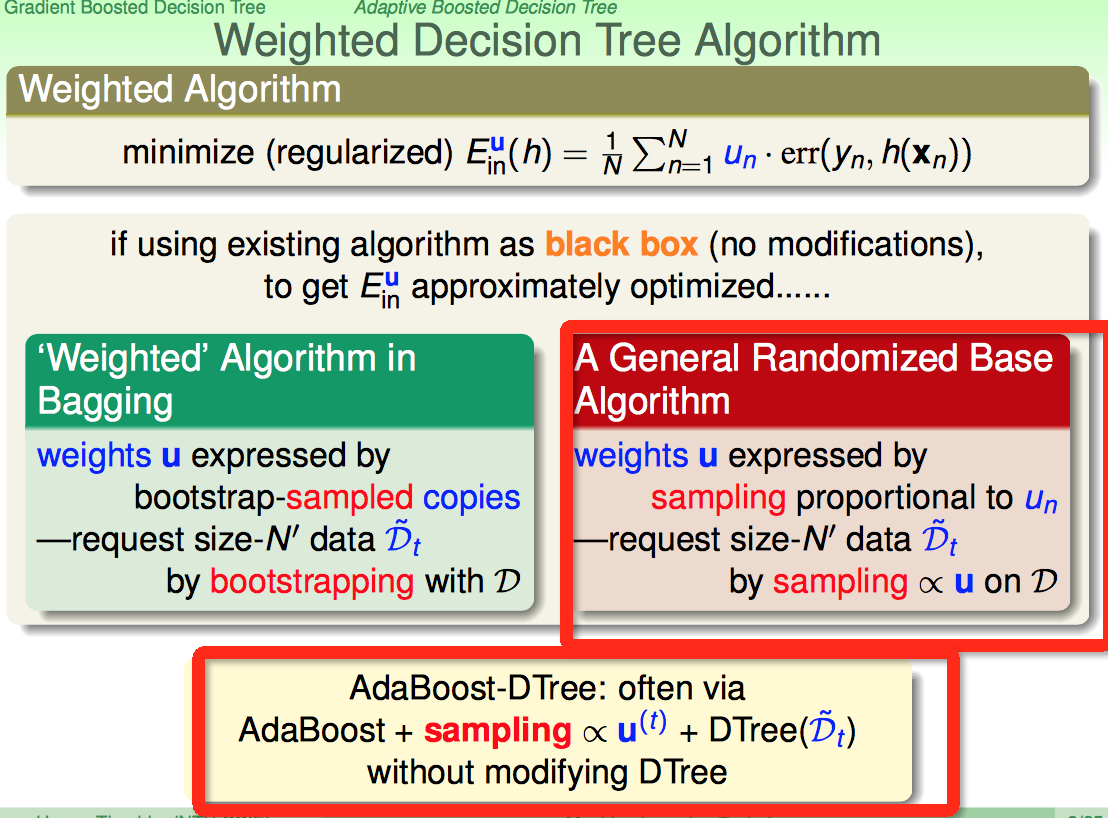
回想bagging的weighted策略：每轮boostrapping的时候，样本的权重体现在copy个数上。

现在从一个更一般的角度来看，给定一个weighted u，如果对数据按照u的比例大小对样本进行sampling的动作，那么最后D中的数据也体现了weighted。

这样AdaBoost-DTree的原型就出来了：

1）AdaBoost方法

2）按照给定的权重对样本进行sampling的动作，生成每棵树的训练数据

3）训练每棵树

这种方法如果不限制树的高度，是容易产生autocracy的。原因是如果把所有的资料丢进去，容易全切开。

这里产生一个疑问：为什么random forest中每棵树就不会有这种完全切开全分开的情况，甚至在decision stump那个作业的时候，会不会有某个stump给全切开了。

1）个人感觉random forest样本、特征、分支条件（b(x)）都是randomness的，完全分开的可能性极小极小

2）至于decision stump，如果真有个decision stump能一刀切开，那也就不用这么复杂的模型了

总的来说，每棵树要弱一些。

如果弱到不能再弱，树就只留下一层了，这时候decision tree就退化成了decision stump了。

接下来，林开始讲解AdaBoost方法的一些optimization view以及内在的insights，这里的一些推导大体思路记住就可以了。

AdaBoost的核心是每个样本的权重变化，所谓的insights也是从这里出发。

1）把之前讲授的AdaBoost样本权重迭代公式转换一下形式（重点是引入了alphat）：

　　unt+1 = unt * exp(-yn * alphat * gt(xn))

2）根据修改后的迭代公式，给出了每个样本在T+1轮的权重通项公式：

　　unT+1 = 1/N * exp(- yn * Σt=1,T (alphat * gt(xn)) )

　　（这里有个地方在之前提到过，一般N个样本，每个样本的初始权重系那个灯，都是1/N）

综合上面两点，unT+1 与 前面T轮产生的所有gt对样本点xn的综合打分情况（Σt=1,T (alphat * gt(xn))） 有关系。

林在这里点出了一个insights：可以把voting score和margin联系起来，类比SVM中的margin概念。

1）把每个gt(xn)看成是xn的一种transform，前面的alphat看成是transformed之后的权重

2）这种形式很像hard-margin SVM中的margin

我们肯定是希望yn*(voting score)越大越好，因为这代表预测值跟实际值更靠近；因此我们可以得到unT+1有可能随着T增加而变小。

顺着这种思路，AdaBoost的大方向最起码应该是unT+1越小越好，那么Σn=1,N(unt)也应该是随着AdaBoost的迭代而逐步减小的。

因此，思路就是：预测的准 → yn*(voting score)越大越好 → ΣunT+1越小越好

于是，AdaBoost的优化目标函数就可以大概给出来了。

再次请出来我们的老朋友error0/1，对比一下AdaBoost又产生了一个bound住error0/1的上界的error measure，叫“exponential error measure”

如下图：

既然目标函数大概写出来了，下面就是怎么最小化这个目标函数了。

这个任务比较麻烦，因为是Σ套着exp再套着Σ，因此需要一些前人的智慧了。

模仿gradient descent的方法，假设前面已经AdaBoost完t-1轮了，现在要求的是一个函数gt(x)（或者称为h(x)）。

再第t轮，我们沿着函数h(x)的方向走ita的步长，可以使得目标函数迅速往min的方向走。如下：

1）由于前面已经执行完了t-1轮，因此可以把式子化简一下，把一些项目合并成unt的函数形式

2）利用xn=0点的泰勒展开，进一步化简（这里为什么要用0这个位置的taylor展开呢，可以理解成h(x)只是沿着原来的Σ1,t-1(alphat*g'(xn)这个函数，挪动的了一小步；这一小步，就意味着变化很小，变化很小甚至接近0，因此就可以在0点taylor展开。不晓得这种理解是否正确，意会吧）

到此，我们利用前人的智慧已经把目标函数给大大简化了，要求的东西有俩：

1）h(x)是啥？

2）ita是啥？

这里的方法还是挺巧妙的

1）先提出来一个固定的Σunt，后面留出来的“变化的一项”

2）再分析下后面变化的这一项，如果要后面变化这一项最小，那么就是最小化Einu(h)（周边再配合上一些常系数）

因此，可以获得结论：在AdaBoost的过程中，算法A就是good gt了！

下面再看ita如何求。

核心在于EADA是怎么变成可对ita求导的形式的：

EADA = u1t*exp(-ita) + u2t*exp(ita)...

EADA1 = u1t*exp(-ita) + ut2t*0 ... （EADA1只考虑exp(-ita)的项，其余的补上0）

EADA2 = u1t*0 + u2t * exp(ita) ...（EADA2只考虑exp(+ita)的项，其余的补上0）

则，EADA = EADA1 + EADA1 = (Σunt) * ( (1-epson)exp(-ita) + epson*exp(ita) )

随后的求导步骤就是很自然的了，因此就验证了之前的结论，itat = sqrt( (1-epsont)/epsont) )就是最优的。前一次课直接给出了这个结论，并没有说为什么，这次算是给出了一个相对理论些的推导。

再往更一般的Gradient Boost推广。

推广的方式就是泛化error measure function，如下：

沿着这个思路，下面往regression的方向上平移一下。

大体的目标还是两个：

1）求解函数h(x)的形式

2）求解函数h(x)移动的幅度

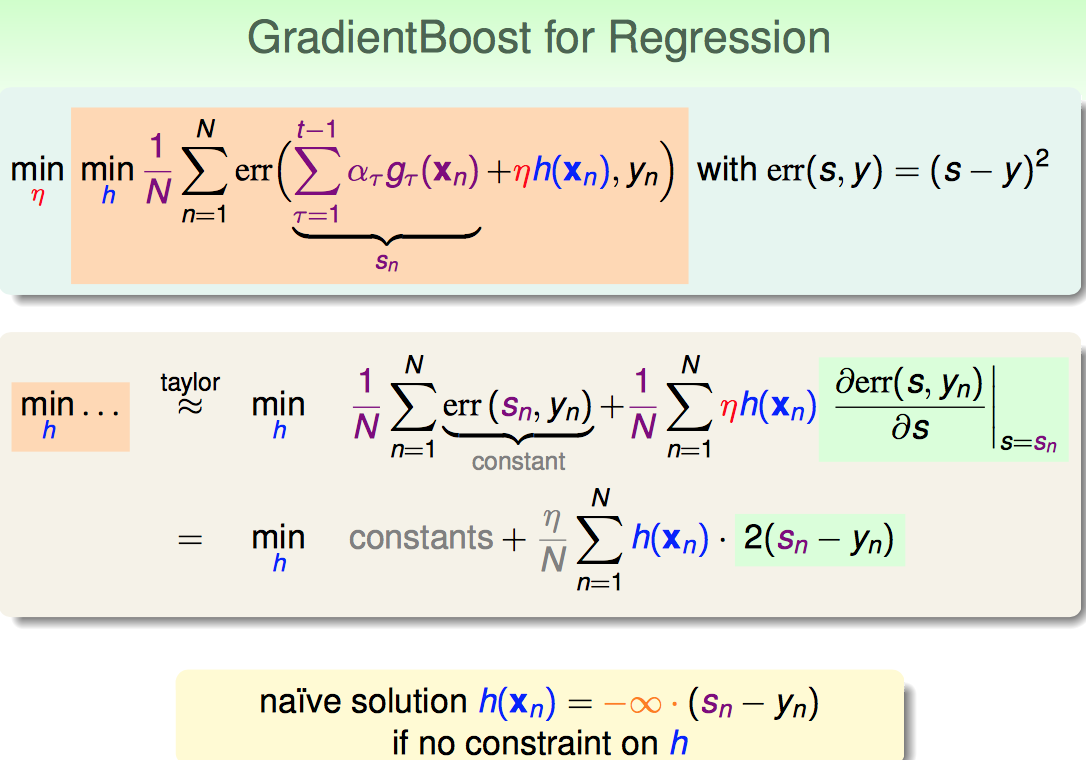
先搞定h(x)的形式

regression一般用square error，直接上taylor：

1）前面一项是constant，因为yn都知道sn也都知道

2）第二项要对s求导 并在sn这点取导数值

这样，看起来貌似h(x)无穷大；这样不科学，于是要添加对于h(x)的惩罚项。

再经过penalize一番折腾之后，h终于有个像模像样的形式了：即regression with residuals。

接下来再解决移动幅度的问题。

一番云雨之后，alphat也求出来了，就是一个单变量的线性回归。

把前面的铺垫都做好了之后，简练地给出了GBDT的形式：

1）利用C&RT去学{x, yn-sn}，保留这一轮学出来的树gt(x)

2）再求{gt(x), residual}线性回归，最小化目标函数求出来ita

3）更新sn

学习足够多次数后，返回组合的GBDT。

最后，林对几种经典的aggregation模型进行了汇总。

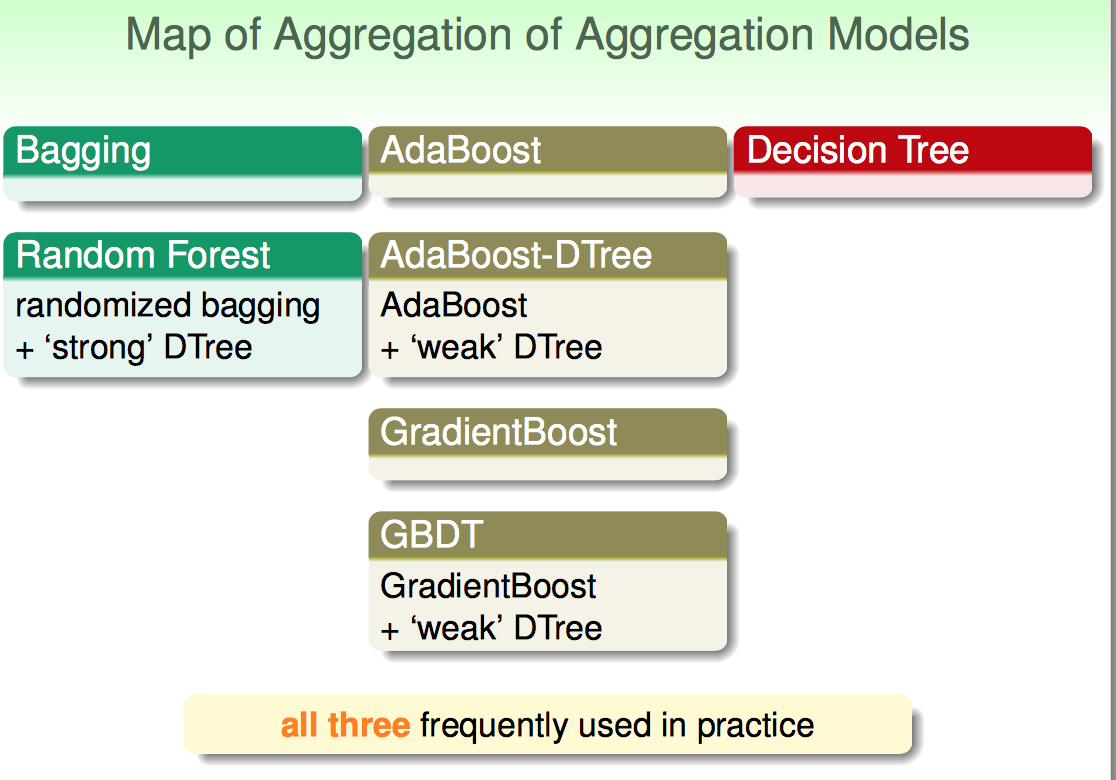
Random Forest: 代表bagging+强子模型

AdaBoost DTree 或 GBDT ：代表AdaBoost+弱子模型

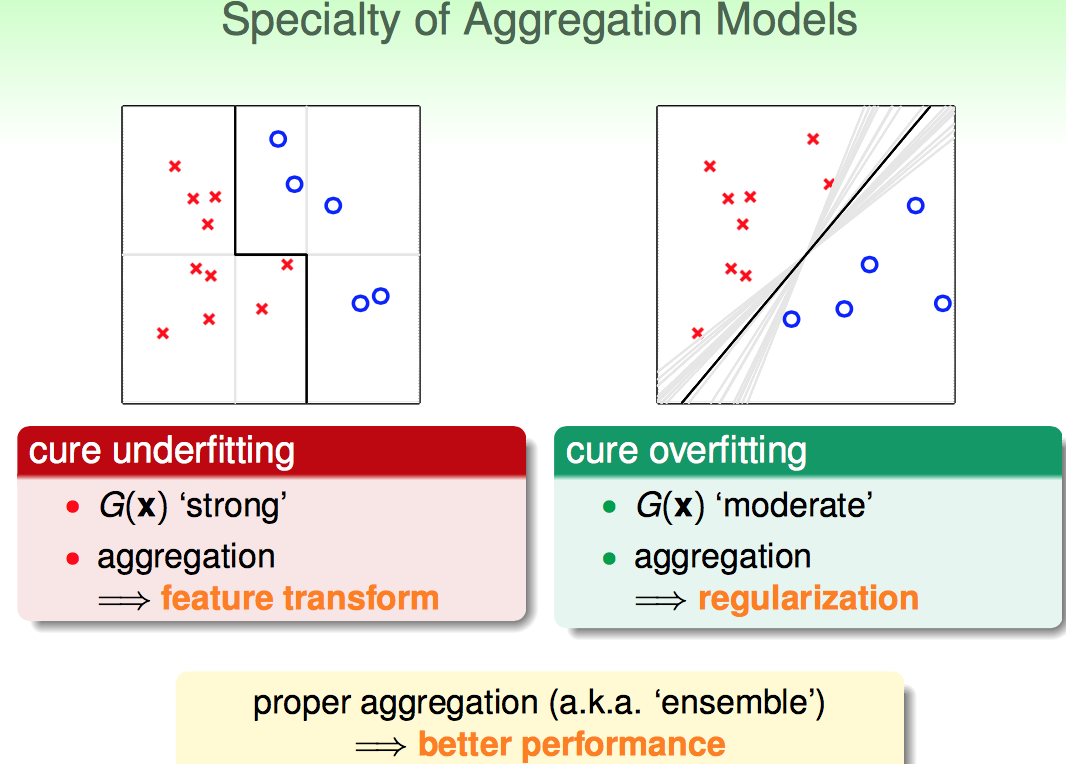
AdaBoost系列的方法：把弱的拼在一起，组成一个强的G(x)；背后的insights可以理解为，利用很多弱弱的模型做了特征转换，转化后再合并在一起就变强了。

RF系列的方法：把本身很强的拼在一起，通过diversity达到regularization的效果（有的子模型往正的方向强，有的往负的方向强，多搞一些这样的模型就中和了彼此的overfitting，类似SVM large margin的效应）