在ArcGIS Desktop中进行三参数或七参数精确投影转换

转自 在ArcGIS Desktop中进行三参数或七参数精确投影转换

 

 

ArcGIS中定义的投影转换方法，在对数据的空间信息要求较高的工程中往往不能适用，有比较明显的偏差。在项目的前期数据准备工作中，需要进行更加精确的三参数或七参数投影转换。下面介绍两种办法来在ArcGIS Desktop中进行这种转换。

在ArcMap中进行动态转换

假设原投影坐标系统为Xian80坐标系统，本例选择为系统预设的Projected Coordinate Systems\Gauss Kruger\Xian 1980\Xian 1980 GK Zone 20投影，中央经线为117度，要转换成Beijing 1954\Beijing 1954 GK Zone 20N。

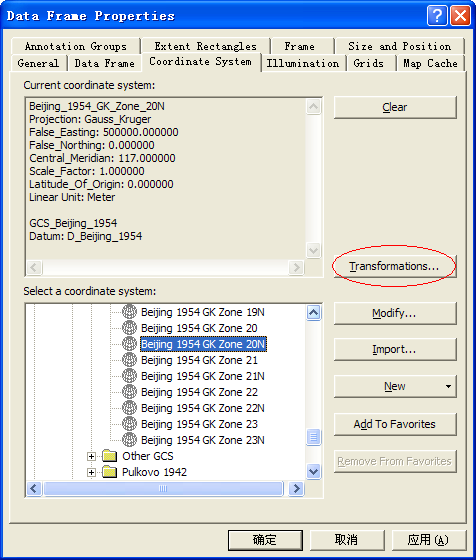
在ArcMap中加载了图层之后，打开View-Data Frame Properties对话框，显示当前的投影坐标系统为Xian
1980 GK Zone 20，在下面的选择坐标系统框中选择Beijing 1954 GK Zone
20N，在右边有一个按钮为Transformations...

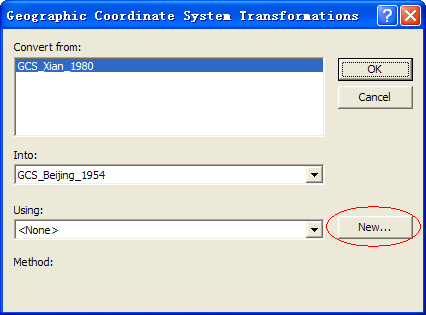
点击打开一个投影转换对话框，可以在对话框中看到Convert
from和Into表明了我们想从什么坐标系统转换到什么坐标系统。

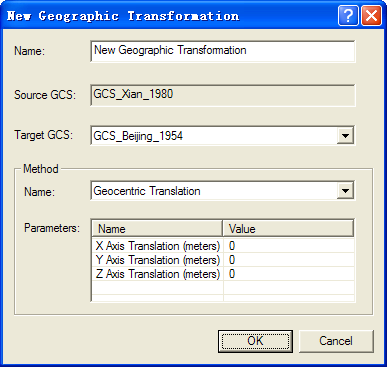
在下方的using下拉框右边，点击New...，新建一个投影转换公式，在Method下拉框中可以选择一系列转换方法，其中有一些是三参数的，有一些是七参数的，然后在参数表中输入各个转换参数。

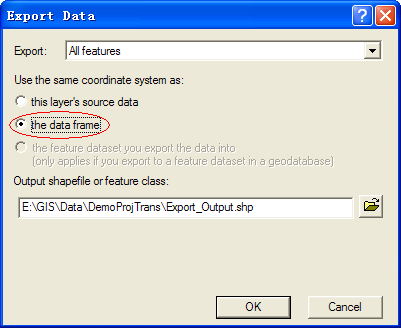
输入完毕以后，点击OK，回到之前的投影转换对话框，再点击OK，就完成了对当前地图的动态投影转换。这时还没有对图层文件本身的投影进行转换，要转换图层文件本身的投影，再使用数据导出，导出时选择投影为当前地图的投影即可。

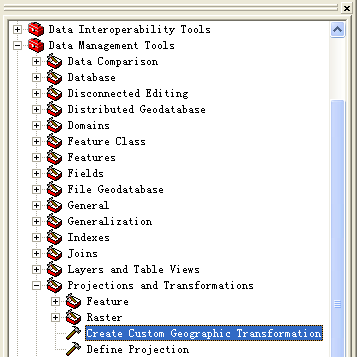
方法2：对于有大量图层需要进行投影转换时，这种手工操作的办法显得比较繁琐，每次都需要设置参数。可以只定义一次投影转换公式，而在此后的转换中引用此投影转换公式即可。这种方法需要在ArcTools中进行操作。在Data
Management Tools\Projections and Tranformations\下，有Create Custom
Geographic Transformation命令。

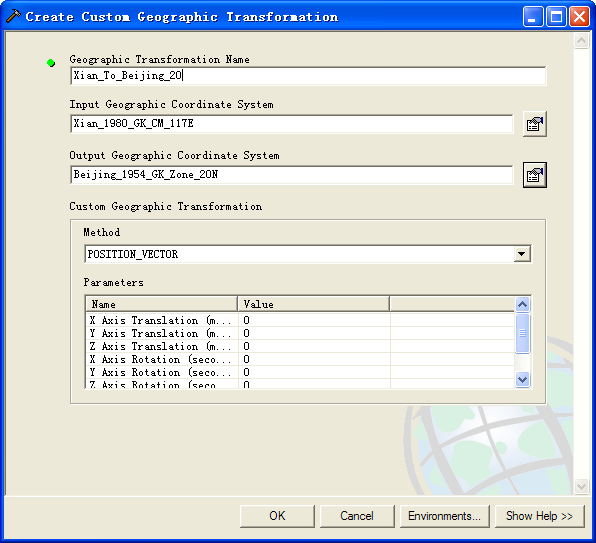
打开这个命令，选择输入和输出的投影，可以是系统自带的也可以是自己设置的，选择转换方法，与方法１种介绍的类似，可选择三参数或者七参数，然后输入各个参数指。通过为这个投影转换公式指定一个名称，可以在以后的操作中直接引用此公式而不用重复输入各个参数了。点击OK生成这个投影转换公式。

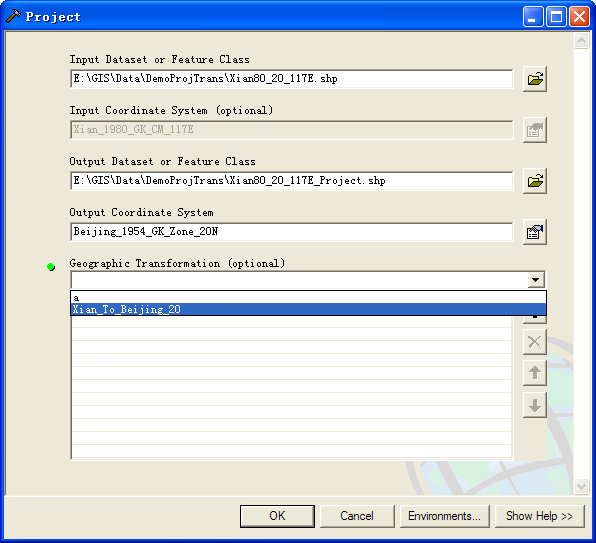
在方法一里面，我们是动态的改变了地图的投影，然后通过数据导出的办法将要转换投影的图层重新生成的。在这里，我们可以直接使用Data
Management Tools\Projections and
Tranformations\下的Project命令，生成转换后的图层文件，Project命令分别位于Feature和Raster目录下，分别针对于矢量和栅格数据。在这个命令中，在指定了输入的图层后，Input
Coordinate
System自动的识别出了输入的投影，需要用户指定输出的投影，如果两者与之前定义投影转换公式的输入和输入投影的话，在下面的Geographic
Transformation下拉框中会出现之前定义的公式名称，直接选择即可使用。

点击OK以后就可以直接生成这个图层文件而不需要进一步的操作了。

 

坐标转换三参数计算器为一款在北京54坐标系、西安80坐标系、WGS84坐标系、国家2000不同坐标系之间（非同一椭球体）三参数条件下的局部范围（900km2）坐标转换软件，具有批量坐标转换功能，通过一个已知公共点(同时具有两套坐标系坐标的点)就能转换，避免了七参数要收集三个公共点的困扰。兼有导航型手持GPS的54坐标、西安80坐标系下DA、DF、DX、DY、DZ参数设置的精确计算功能，帮助手持GPS用户提高野处定点精度；同时本软件也是目前大多数GPS手机所定位的经纬度坐标转换成北京54和西安80坐标的最佳帮手。

 

 

GPS三参数，四参数，七参数的区别？

首先说七参，就是两个空间坐标系之间的旋转，平移和缩放，这三步就会产生必须的七个参数，平移有三个变量Dx，Dy，DZ；旋转有三个变量，再加上一个尺度缩放，这样就可以把一个空间坐标系转变成需要的目标坐标系了，这就是七参的作用。如果说你要转换的坐标系XYZ三个方向上是重合的，那么我们仅通过平移就可以实现目标，平移只需要三个参数，并且现在的坐标比例大多数都是一致的，缩放比默认为一，这样就产生了三参数，三参就是七参的特例，旋转为零，尺度缩放为一。四参是应用在两个平面之间转换的，还没有形成统一的标准。

三参数与七参数的区别
http://wenku.baidu.com/view/601093563c1ec5da50e2701e.html

 

这个参数不同是因为北京54坐标系为参心大地坐标系，大地上的一点可用经度L54、纬度M54和大地高H54定位，它是以克拉索夫斯基椭球为基础，经局部平差后产生的坐标系.它采用了前苏联的克拉索夫斯基椭球参数，并与前苏联1942年坐标系进行联测，通过计算建立了我国大地坐标系，定名为1954年北京坐标系。因此，1954年北京坐标系可以认为是前苏联1942年坐标系的延伸。它的原点不在北京而是在前苏联的普尔科沃。东经30°19′15〃，北纬59°46′6〃。

而80坐标系是1980年国家大地坐标系采用地球椭球基本参数为1975年国际大地测量与地球物理联合会第十六届大会推荐的数据。该坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇，位于西安市西北方向约60公里，故称1980年西安坐标系，又简称西安大地原点。基准面采用青岛大港验潮站1952－1979年确定的黄海平均海水面（即1985国家高程基准）。

西安80坐标系与北京54坐标系其实是一种椭球参数的转换作为这种转换在同一个椭球里的转换都是严密的，而在不同的椭球之间的转换是不严密，因此不存在一套转换参数可以全国通用的，在每个地方会不一样，因为它们是两个不同的椭球基准

七参数个人理解：

第一：地球不是真正的球形，所以各个地方的坐标值相对于正规的球体有些偏差，因此有了七参数，以得到精确的坐标值

第二：数据保密。七参数的标准各个地方，各有不同，并且是绝对保密的。目的就是为了防止他国窃取精确数据资料。

坐标系统之间的坐标转换既包括不同的参心坐标之间的转换，或者不同的地心坐标系之间的转换，也包括参心坐标系与地心坐标系之间的转换以及相同坐标系的直角坐标与大地坐标之间的坐标转换，还有大地坐标与高斯平面坐标之间的转换。在两个空间角直坐标系中，假设其分别为O--XYZ和O--XYZ，如果两个坐标系的原来相同，通过三次旋转，就可以两个坐标系重合；如果两个直角坐标系的原点不在同一个位置，通过坐标轴的平移和旋转可以取得一致；如果两个坐标系的尺度也不尽一致，就需要再增加一个尺度变化参数；而对于大地坐标和高斯投影平面坐标之间的转换，则需要通过高斯投影正算和高斯投影反算，通过使用中央子午线的经度和不同的参考椭球以及不同的投影面的选择来实现坐标的转换。

WGS84与BJ54是两种不同的大地基准面，不同的参考椭球体，因而两种地图下，同一个点的坐标是不同的，无论是三度带六度带坐标还是经纬度坐标都是不同的。当要把GPS接收到的点（WGS84坐标系统的）叠加到BJ54坐标系统的底图上，那就会发现这些GPS点不能准确的在它该在的地方，即“与实际地点发生了偏移”。这就要求把这些GPS点从WGS84的坐标系统转换成BJ54的坐标系统了。

在不同的椭球之间的转换是不严密的。那么，两个椭球间的坐标转换应该是怎样的呢？一般而言比较严密的是用七参数法，即3个平移因子（X平移，Y平移，Z平移），3个旋转因子（X旋转，Y旋转，Z旋转），一个比例因子（也叫尺度变化K）。国内参数来源的途径不多，一般当地测绘部门会有。通行的做法是：在工作区内找三个以上的已知点，利用已知点的BJ54坐标和所测WGS84坐标，通过一定的数学模型，求解七参数。若多选几个已知点，通过平差的方法可以获得较好的精度。如果区域范围不大，最远点间的距离不大于30Km（经验值），这可以用三参数，即只考虑3个平移因子（X平移，Y平移，Z平移），而将旋转因子及比例因子（X旋转，Y旋转，Z旋转，尺度变化K）都视为0，所以三参数只是七参数的一种特例。北京54和西安80也是两种不同的大地基准面，不同的参考椭球体，他们之间的转换也是同理。在ArcGIS中提供了三参数、七参数转换法。而在同一个椭球里的转换都是严密的，在同一个椭球的不同坐标系中转换需要用到四参数转换，举个例子，在深圳既有北京54坐标又有深圳坐标，在这两种坐标之间转换就用到四参数，计算四参数需要两个已知点。

 

七参数估计
(课件):
第七章参数估计统计推断的基本问题可以分为两大类,一类是估计问题,另一类是假设检验问题.本章讨论总体参数的点估计和区间估计.第一节点估计定义1：设总体X的分布函数的形式已知，但它的一个或者多个参数未知,借助总体X的一个样本来估计总体未知参数的值的问题称为参数的点估计问题.1、矩估计法用样本矩作为总体矩的估计，当总体X的分布类型已知，但含有未知参数，可以用矩估计法获得未知参数的估计。在例题中,我们采用了样本均值来估计总体均值.下面介绍两种常用的构造估计量的方法：矩估计法和极大似然估计法.2、极(最)大似然估计(1)似然函数(a)离散型总体(b)连续型总体(2)极大似然估计例
6 求均匀分布U[θ1 ,θ2]中参数θ1
,θ2极大似然估计.解先写出似然函数该似然函数不连续，不能用似然方程求解方法，只有回到极大似然估计原始定义，注意最大值只能发生在第二节估计量的评价准则1、无偏性2、有效性第三节区间估计...

三参数就是尺度比为0、旋转为0的七参数，属于椭球转换，四参数是平面转换。

GPS导航时一般使用三参数就可以达到较高精度，七参数太麻烦而且不实用。

两个椭球间的坐标转换应该是怎样的呢？一般而言比较严密的是用七参数法（包括布尔莎模型，一步法模型，海尔曼特等），即X平移，Y平移，Z平移，X旋转，Y旋转，Z旋转，尺度变化K。要求得七参数就需要在一个地区需要3个以上的已知点，如果区域范围不大，最远点间的距离不大于30Km(经验值)，这可以用三参数（莫洛登斯基模型），即X平移，Y平移，Z平移，而将X旋转，Y旋转，Z旋转，尺度变化K视为0，所以三参数只是七参数的一种特例。

WGS-84和BJ-54都需要用经纬度，我经常用

输入经纬度后 按convert可以计算三参数，transform是椭球转换
比如，广东部分地区的84转54的三参数为0、143.6、74.3
输入2组经纬度后按convert就可以了，因为是美国的软件，所以不支持直角坐标，84和54坐标经纬度一般差2秒左右

软件里面的from和to两个椭球的选择要正确，北京坐标选择krassovsky

 

 

利用ArcGIS进行地图投影和坐标转换的方法

1、动态投影(ArcMap)
所谓动态投影指，ArcMap中的Data
的空间参考或是说坐标系统是默认为第一加载到当前工作区的那个文件的坐标系统，后加入的数据，如果和当前工作区坐标系统不相同，则ArcMap会自动做投影变换，把后加入的数据投影变换到当前坐标系统下显示！但此时数据文件所存储的数据并没有改变，只是显示形态上的变化！因此叫动态投影！表现这一点最明显的例子就是，在Export
Data时，会让你选择是按this layer's source data（数据源的坐标系统导出），还是按照the Data
（当前数据框架的坐标系统）导出数据！
2、坐标系统描述(ArcCatalog)
大家都知道在ArcCatalog中可以一个数据的坐标系统说明！即在数据上鼠标右键->Properties->XY
Coordinate
System选项卡，这里可以通过modify，Select、Import方式来为数据选择坐标系统！但有许多人认为在这里改完了，数据本身就发生改变了！但不是这样的！这里缩写的信息都对应到该数据的.aux文件！如果你去把该文件删除了，重新查看该文件属性时，照样会显示Unknown！这里改的仅仅是对数据的一个描述而已，就好比你入学时填写的基本资料登记卡，我改了说明但并没有改变你这个人本身！因此数据文件中所存储的数据的坐标值并没有真正的投影变换到你想要更改到的坐标系统下！

但数据的这个描述也是非常重要的，如果你拿到一个数据，从ArcMap下所显示的坐标来看，像是投影坐标系统下的平面坐标，但不知道是基于什么投影的！因此你就无法在做对数据的进一不处理！比如：投影变换操作！因为你不知道要从哪个投影开始变换！

因此大家要更正一下对ArcCatalog中数据属性中关于坐标系统描述的认识！

3、投影变换(ArcToolBox)

上面说了这么多，要真正的改变数据怎么办，也就是做投影变换！在ArcToolBox->Data
Management Tools->Projections and
Transformations下做！
在这个工具集下有这么几个工具最常用，
1、Define Projection
2、Feature->Project
3、Raster->Project Raster 4、Create Custom Geographic
Transformation
当数据没有任何空间参考时，显示为Unknown！时就要先利用Define Projection来给数据定义一个Coordinate
System，然后在利用Feature->Project或Raster->Project
Raster工具来对数据进行投影变换！

由于我国经常使用的投影坐标系统为北京54,西安80！由这两个坐标系统变换到其他坐标系统下时，通常需要提供一个Geographic
Transformation，因为Datum已经改变了！这里就用到我们说常说的转换3参数、转换7参数了！而我们国家的转换参数是保密的！因此可以自己计算或在购买数据时向国家测绘部门索要！知道转换参数后，可以利用Create
Custom Geographic
Transformation工具定义一个地理变换方法，变换方法可以根据3参数或7参数选择基于GEOCENTRIC_TRANSLATION和COORDINATE_方法！

这样就完成了数据的投影变换！数据本身坐标发生了变化！
当然这种投影变换工作也可以在ArcMap中通过改变Data 的Coordinate System来实现，只是要在做完之后在按照Data
的坐标系统导出数据即可！

方法一：在Arcmap中转换：
1 加载要转换的数据，右下角为经纬度
2 点击视图à数据框属性à坐标系统
3 导入或选择正确的坐标系，确定。这时右下角也显示坐标。但数据没改变
4 右击图层à数据à导出数据
5 选择第二个（数据框架），输出路径，确定。
6 此方法类似于投影变换。
方法二：在forestar中转换：
1 用正确的坐标系和范围新建图层aa
2 打开要转换的数据，图层输出与原来类型一致，命名aa，追加。
方法三：在ArcToolbox中转换：
1 管理工具à投影（project），选择输入输出路径以及输出的坐标系
2 前提是原始数据必须要有投影

 

地理坐标系和投影坐标系的区别

经常碰到这两个概念：
Geographic coordinate system 和 projected coordinate
system

1、首先理解Geographic
coordinate system，Geographic coordinate system直译为地理坐标系统(大地坐标系)
，是以经纬度为地图的存储单位的。
很明显，Geographic coordinate
system是球面坐标系统。我们要将地球上的数字化信息存放到球面坐标系统上，如何进行操作呢？地球是一个不规则的椭球，如何将数据信息以科学的方法存放到椭球上？这必然要求我们找到这样的一个椭球体。这样的椭球体具有特点：可以量化计算的。

具有长半轴，短半轴，偏心率。以下几行便是Krasovsky_1940椭球及其相应参数。
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000
然而有了这个椭球体以后还不够，还需要一个大地基准面将这个椭球定位。在坐标系统描述中，可以看到有这么一行： Datum:
D_Beijing_1954表示，大地基准面是D_Beijing_1954。
有了Spheroid和Datum两个基本条件，地理坐标系统便可以使用。完整参数：

Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian: Greenwich (0.000000000000000000)
Datum: D_Beijing_1954
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000

2、接下来便是Projection coordinate system（投影坐标系统），首先看看投影坐标系统中的一些参数。

Projection: Gauss_Kruger
Parameters:
False_Easting: 500000.000000
False_Northing: 0.000000
Central_Meridian: 117.000000（6度带20号带中央子午线或者3度带39号带的中央经线）
Scale_Factor: 1.000000
Latitude_Of_Origin: 0.000000
Linear Unit: Meter (1.000000)
Geographic Coordinate System:
Name: GCS_Beijing_1954
Alias:
Abbreviation:
Remarks:
Angular Unit: Degree (0.017453292519943299)
Prime Meridian: Greenwich (0.000000000000000000)
Datum: D_Beijing_1954
Spheroid: Krasovsky_1940
Semimajor Axis: 6378245.000000000000000000
Semiminor Axis: 6356863.018773047300000000
Inverse Flattening: 298.300000000000010000

从参数中可以看出，每一个投影坐标系统都必定会有Geographic Coordinate System。
投影坐标系统，实质上便是平面坐标系统，其地图单位通常为米。那么为什么投影坐标系统中要存在坐标系统的参数呢？这时候，又要说明一下投影的意义：将球面坐标转化为平面坐标的过程便称为投影。好了，投影的条件就出来了：

a、球面坐标 b、转化过程（也就是算法）
也就是说，要得到投影坐标就必须得有一个“拿来”投影的球面坐标，然后才能使用算法去投影！即每一个投影坐标系统都必须要求有Geographic
Coordinate System参数。
备注：

Alias: 别名
Abbreviation: 缩写
Remarks: 备注
Projection: Gauss_Kruger 投影 高斯-克吕格
Parameters: 参数
False_Easting: 500000.000000 伪东
False_Northing: 0.000000 伪北
Central_Meridian: 105.000000中央经线
Scale_Factor: 1.000000 比例因子
Latitude_Of_Origin: 0.000000 纬度原点
Linear Unit: Meter (1.000000) 单位 米
Geographic Coordinate System: 地理坐标系
Name: GCS_Beijing_1954 高斯-克吕格 Beijing_1954
Alias: 别名
Abbreviation: 缩写
Remarks: 备注
Angular Unit: Degree (0.017453292519943299) 角度 单位
Prime Meridian: Greenwich (0.000000000000000000) 子午线
Datum: D_Beijing_1954 大地基准面
Spheroid: Krasovsky_1940 椭球体   克拉索夫斯基1940
    Semimajor Axis: 6378245.000000000000000000 长半轴
    Semiminor Axis: 6356863.018773047300000000 短半轴
    Inverse Flattening: 298.300000000000010000 偏心率