洛谷 P1439 【模板】最长公共子序列LCS 解题报告

题目传送门

是一道十分经典的LCS问题

很容易想到 n 的一般算法：
主题代码如下：

for (int i = 1; i <= n; i++)
      for (int j = 1; j <= n; j++){
      	dp[i][j] = max (dp[i-1][j], dp[i][j-1]);
      	if (a[i] == b[j]) dp[i][j] = max (dp[i][j], dp[i-1][j-1] + 1);
	  }
  printf ("%d", dp[n][n]);　

但往下看一眼数据范围 ：

没错， n ≤100000 ，n²直接TLE

题目描述中提到了两组数都是 自然数1-n的一个排列

所以这题可以这么来做：

设两个数组分别为 a 和 b

对于每一个a数组中的数，一定有一个唯一对应的相等的b数组中的数

可以将a数组中的数看作 1,2,3,4,5......n

将b数组中的数也变为对应的值，假设变为数组c，可以发现，这变成了一个最长上升子序列LIS问题

当c中的数有一个上升子序列时，则这个序列在原数组中一定与a数组是公共的

模拟一遍样例：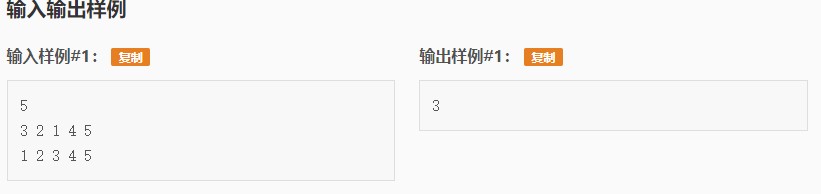

先把第一列数看作 1， 2， 3， 4， 5。 则3对应1， 2对应2， 1对应3 .......

第二列数变为 3， 2， 1， 4， 5

最长上升子序列为 1， 4， 5 或 2， 4， 5或3， 4， 5

可以发现，这三个序列在原数组中都能找到相应的公共部分

所以答案为3

完整代码：

#include <bits/stdc++.h>
using namespace std;
#define f(i, r)  for (int i = 1; i <= r; i++)
int n, x, a[100005], k[100005], len, q[100005];
int main(){
	scanf ("%d", &n);
	f (i, n) scanf ("%d", &x), k[x] = i;
    f (i, n) scanf ("%d", &a[i]), a[i] = k[a[i]];
	f (i, n){
		if (a[i] > q[len]) q[++len] = a[i];
		else{
			int w = upper_bound (q + 1, q + len + 1, a[i]) - q;
			q[w] = a[i];
		}
	}
	printf ("%d", len);
	return 0;
}

点一下左边的推荐吧！谢谢~~~