Educational Codeforces Round 37 E. Connected Components?（图论）

E. Connected Components?

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given an undirected graph consisting of n vertices and 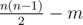 edges. Instead of giving you the edges that exist in the graph, we give you m unordered pairs (x, y) such that there is no edge between x and y, and if some pair of vertices is not listed in the input, then there is an edge between these vertices.

You have to find the number of connected components in the graph and the size of each component. A connected component is a set of vertices X such that for every two vertices from this set there exists at least one path in the graph connecting these vertices, but adding any other vertex to X violates this rule.

Input

The first line contains two integers n and m (1 ≤ n ≤ 200000, ).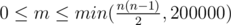

Then m lines follow, each containing a pair of integers x and y (1 ≤ x, y ≤ n, x ≠ y) denoting that there is no edge between x and y. Each pair is listed at most once; (x, y) and (y, x) are considered the same (so they are never listed in the same test). If some pair of vertices is not listed in the input, then there exists an edge between those vertices.

Output

Firstly print k — the number of connected components in this graph.

Then print k integers — the sizes of components. You should output these integers in non-descending order.

Example

input

5 5
1 2
3 4
3 2
4 2
2 5

output

2
1 4 

题意：一个完全图去掉m条边，求剩下的图的联通块数和每个联通块的大小。

解析:我们先把所有的节点挂链，将当前第一个节点入队，遍历其在原图上相邻的点并做上标记，那么这时没有打上标记的点在补图上和当前节点一定有边相连因而一定在同一个联通块中，所以将没标记的点入队，并且在链表中除去，继续这个过程，直到队列为空时这个联通块就找出来了。把链接的点再删除标记，再取链表上还存在的点入队寻找一个新的联通块，直到删掉所有点为止，复杂度降为了O(n + m)。

代码：

 #include "bits/stdc++.h"
 #define db double
 #define ll long long
 #define vec vector<ll>
 #define Mt  vector<vec>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 #define inf 0x3f3f3f3f
 #define rep(i, x, y) for(int i=x;i<=y;i++)
 const int N   = 1e6 + ;
 const int mod = 1e9 + ;
 const int MOD = mod - ;
 const db  eps = 1e-;
 const db  PI  = acos(-1.0);
 using namespace std;
 int n,m,cnt;
 int hea[N];
 int a[N];
 int pre[N],nex[N],ti[N];
 int id=;
 struct P{
     int fr,to,nxt;
 };
 P e[N];
 void add(int fr,int to){//前向星
     e[cnt].fr=fr,e[cnt].to=to,e[cnt].nxt=hea[fr];
     hea[fr]=cnt++;
 }
 void init()//初始化
 {
     memset(a,, sizeof(a));
     memset(nex,, sizeof(nex));
     memset(ti,, sizeof(ti));
     memset(pre,, sizeof(pre));
     memset(hea,-,sizeof(hea));
     cnt=;
 }
 int main()
 {
     init();
     ci(n),ci(m);
     for(int i=;i<m;i++)
     {
         int x,y;
         ci(x),ci(y);
         add(x,y),add(y,x);
     }
     nex[]=;
     for(int i=;i<=n;i++) pre[i]=i-,nex[i]=i+;//链表
     pre[n+]=n;
     int tot=;
     while(nex[]!=n+)
     {
         queue<int>q;
         int sum=;
         q.push(nex[]);//链表当前第一个节点入队
         nex[]=nex[nex[]];
         pre[nex[]]=;
         while(q.size())
         {
             id++;
             int u=q.front();
             q.pop();
             for(int i=hea[u];i!=-;i=e[i].nxt){//标记与u点直接相连的点
                 int to=e[i].to;
                 ti[to]=id;
             }
             for(int i=nex[];i!=n+;i=nex[i]){//若点未被标记则在补图中直接相连，对此点继续同样的操作。
                 if(ti[i]!=id) nex[pre[i]]=nex[i],pre[nex[i]]=pre[i],q.push(i),sum++;
             }
         }
         a[++tot]=sum;//联通块大小
     }
     sort(a+,a+tot+);
     pi(tot);
     for(int i=;i<=tot;i++) printf("%d%c",a[i],i==tot?'\n':' ');
     return ;
 }