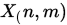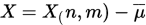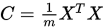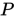PCA降维技术
PCA降维技术
Time: 2017-2-28
主成分分析(PCA)
主成分分析(Principal Component Analysi)是一种掌握可以提取主要特征对的方法,它可以从多元失误中解析出主要影响因素。计算朱成福的目的是将高维数据投影到低维空间。主要是用于降维,提取数据的主要特征分量。
降维,当然以为着信息的丢失,但是鉴于数据本身常常存在相关性,我们可以想办法在降维的同时将信息的随时尽量降低。
PCA Algorithm
主要思想:
利用较少数据的特征对样本进行描述以达到降低特征空间维数的目的,根据样本点在多维空间的位置分布,以样本点在空间中变化最大方向,即方差最大方向,作为差别矢量来实现数据的特征提取。具体可以参考这篇文章 关于K-L变换的部分。
在PCA中,我们要做的是找到一个方向向量,当我们把所有的数据都投射到该向量上时,我们希望投射的平均均方误差尽可能的小。方向向量是一个经过原点的向量,而投射误差是从特征向量向该方向向量垂线的长度。大致的情形如下图

具体步骤:
step 1. 数据:
step 2. 零均值化
step 3. 计算出协方差矩阵
step 4. 计算出协方差矩阵的特征值与特征向量, 可以使用SVD分解来实现
step 5. 取特征值最大的前K个特征向量组成矩阵
step 6. 计算PCA:, Y为降维后的结果
在step 2, 对原始数据进行均值化处理后,不仅消除了指标量纲和数量的影响,而且能更加全面地反映原始数据中各指标的变异程度和相互影响程度的信息
而关于协方差矩阵主要是因为,对于
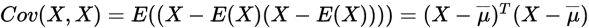 ,当计算自相关(
,当计算自相关(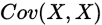 )而协方差计算的主要是数据的相关性质,所以我们可以减少相关性,从而来实现对数据的降维。关于为什么需要使用协方差矩阵可以看这篇文章
)而协方差计算的主要是数据的相关性质,所以我们可以减少相关性,从而来实现对数据的降维。关于为什么需要使用协方差矩阵可以看这篇文章需要注意的是PCA主要是减少投射的平均均方误差,这里需要和线性回归做区别,线性回归主要减少的是最小均方误差。如下图

实例
假设有5条数据,两个特征属性,矩阵的形式如下:

按照上面的算法来实现:
[1]

[2] 均值化:我们可以知道

[3] 计算协方差矩阵

[4] 求特征值 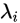 以及特征向量可得
以及特征向量可得
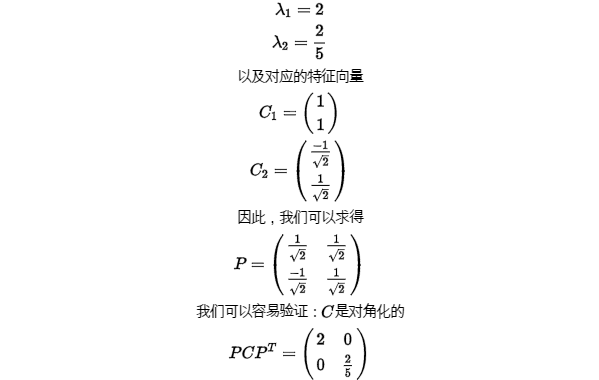
[5] 这里我们取最大的一列,可得到
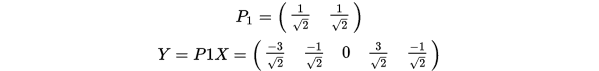
最后我们得到了最终的降维结果如下图

为了更好的观察,把Andrew Ng的课件图拿了过来:

PCA降维技术的更多相关文章
- 机器学习算法-PCA降维技术
机器学习算法-PCA降维 一.引言 在实际的数据分析问题中我们遇到的问题通常有较高维数的特征,在进行实际的数据分析的时候,我们并不会将所有的特征都用于算法的训练,而是挑选出我们认为可能对目标有影响的特 ...
- 降维技术---PCA
数据计算和结果展示一直是数据挖掘领域的难点,一般情况下,数据都拥有超过三维,维数越多,处理上就越吃力.所以,采用降维技术对数据进行简化一直是数据挖掘工作者感兴趣的方向. 对数据进行简化的好处:使得数据 ...
- [机器学习之13]降维技术——主成分分析PCA
始终贯彻数据分析的一个大问题就是对数据和结果的展示,我们都知道在低维度下数据处理比较方便,因而数据进行简化成为了一个重要的技术.对数据进行简化的原因: 1.使得数据集更易用使用.2.降低很多算法的计算 ...
- 数据降维技术(2)—奇异值分解(SVD)
上一篇文章讲了PCA的数据原理,明白了PCA主要的思想及使用PCA做数据降维的步骤,本文我们详细探讨下另一种数据降维技术—奇异值分解(SVD). 在介绍奇异值分解前,先谈谈这个比较奇怪的名字:奇异值分 ...
- 利用PCA降维
参考:<机器学习实战>- Machine Learning in Action 一. 基本思想 PCA(Principal Component Analysis),主成分分析.是目前应用 ...
- 一步步教你轻松学主成分分析PCA降维算法
一步步教你轻松学主成分分析PCA降维算法 (白宁超 2018年10月22日10:14:18) 摘要:主成分分析(英语:Principal components analysis,PCA)是一种分析.简 ...
- 用PCA降维 (Principal Component Analysis,主成分分析)
参考资料:Mastering Machine Learning With scikit-learn 降维致力于解决三类问题.第一,降维可以缓解维度灾难问题.第二,降维可以在压缩数据的同时让信息损失最 ...
- 机器学习(十六)— LDA和PCA降维
一.LDA算法 基本思想:LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的.这点和PCA不同.PCA是不考虑样本类别输出的无监督降维技术. 我们要将数据在低维度上进行投影,投 ...
- [综] PCA降维
http://blog.json.tw/using-matlab-implementing-pca-dimension-reduction 設有m筆資料, 每筆資料皆為n維, 如此可將他們視為一個mx ...
随机推荐
- java 分布式锁
转自:http://www.hollischuang.com/archives/1716 目前几乎很多大型网站及应用都是分布式部署的,分布式场景中的数据一致性问题一直是一个比较重要的话题.分布式的CA ...
- 0420-mysql命令(数据库操作层级,建表,对表的操作)
注意事项: 符号必须为英文. 数据库操作层级: 建表大全: #新建表zuoye1:drop table if exists zuoye1;create table zuoye1( id int ...
- 模拟Queue(wait/notify)
BlockingQueue:顾名思义,首先它是一个队列,并且支持阻塞的机制,阻塞的放入和得到数据.我们要实现LinkedBlockingQueue下面的两个方法put和take. put(anObje ...
- Spring Boot (14) 数据源配置原理
数据源配置源码 这里截取org.springframework.boot.autoconfigure.jdbc.DataSourceConfiguration的部分源码,主要介绍Tomcat和Hika ...
- android黑科技系列——分析某直播App的协议加密原理以及调用加密方法进行协议参数构造
一.前言 随着直播技术火爆之后,各家都出了直播app,早期直播app的各种请求协议的参数信息都没有做任何加密措施,但是慢慢的有人开始利用这个后门开始弄刷粉关注工具,可以让一个新生的小花旦分分钟变成网红 ...
- js-var变量作用域
看代码: var a=10; function fn1(){ alert(a); var a=20; alert(a); } 运行结果:undefined 和 20 注意: 在函数内,变量如没用var ...
- tp实现多语言支持测试
用tp框架实现网页多种语言切换 时间:2016-11-11 浏览次数:1120 编辑:youjiejie 网页如何设计多种语言切换,本文用tp框架实现网页多种语言切换方法结合实例形式较为详细的分析 ...
- HDU_1269_tarjan求强连通分量
迷宫城堡 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submis ...
- MVC 返回404,返回图片,流到数组,apk信息
return HttpNotFound(); byte[] buffer0 = QRCode(); return File(buffer0, @"image/jpeg"); // ...
- Fish:Linux中比bash或zsh更好用的Shell
Fish是一个智能且用户友好的命令行shell,适用于macOS,Linux和其他家族.fish包含语法突出显示.根据你键入字符自动提示autosuggest-as-type和花式选项卡完成等功能,无 ...