机器学习(十一) 支持向量机 SVM(下)
支持向量机通过某非线性变换 φ( x) ,将输入空间映射到高维特征空间。特征空间的维数可能非常高。如果支持向量机的求解只用到内积运算,而在低维输入空间又存在某个函数 K(x, x′) ,它恰好等于在高维空间中这个内积,即K( x, x′) =<φ( x) ⋅φ( x′) > 。那么支持向量机就不用计算复杂的非线性变换,而由这个函数 K(x, x′) 直接得到非线性变换的内积,使大大简化了计算。这样的函数 K(x, x′) 称为核函数
核函数包括线性核函数、多项式核函数、高斯核函数等,其中高斯核函数最常用,可以将数据映射到无穷维,也叫做径向基函数(Radial Basis Function 简称 RBF),是某种沿径向对称的标量函数。 [1] 通常定义为空间中任一点x到某一中心xc之间欧氏距离的单调函数 ,可记作 k(||x-xc||), 其作用往往是局部的,即当x远离xc时函数取值很小。
六、到底什么是核函数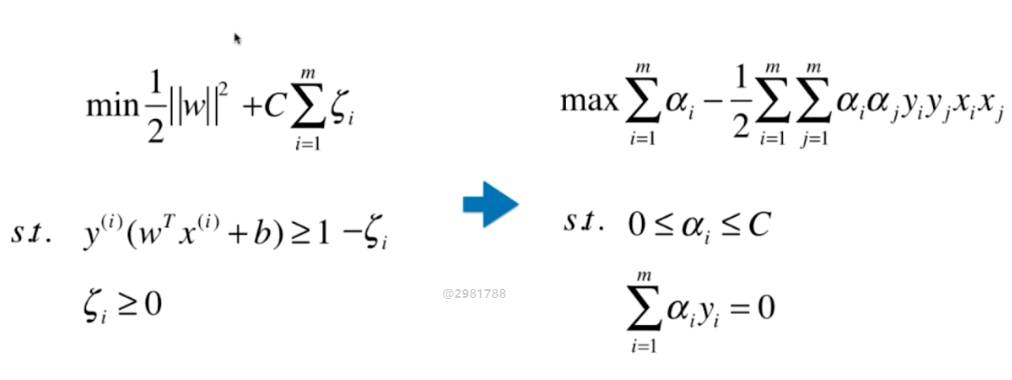
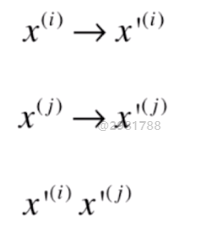





七、RBF核函数









八、RBF核函数中的gamma





九、SVM思想解决回归问题
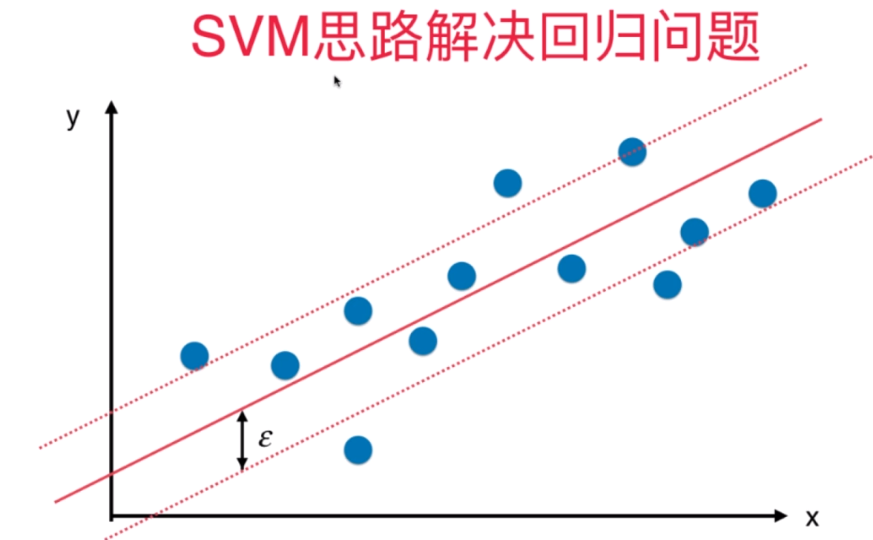
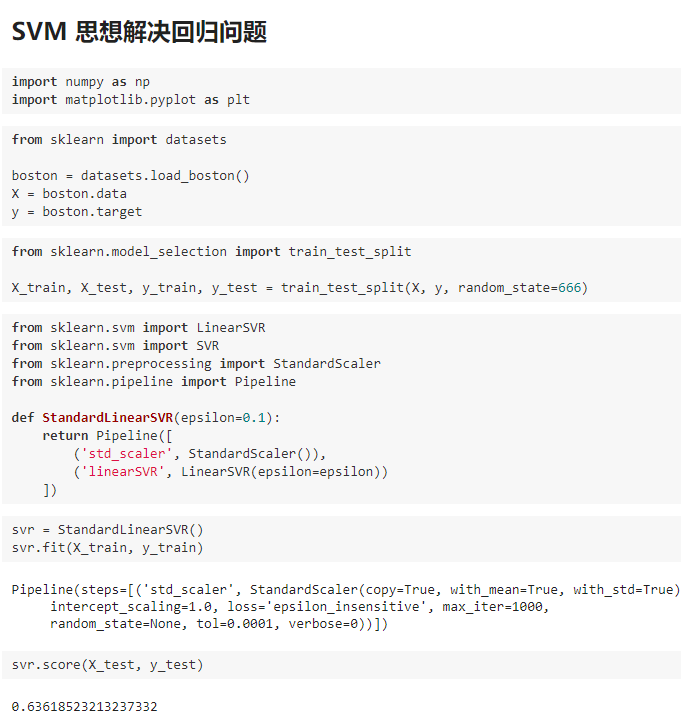
机器学习(十一) 支持向量机 SVM(下)的更多相关文章
- 机器学习(十一) 支持向量机 SVM(上)
一.什么是支撑向量机SVM (Support Vector Machine) SVM(Support Vector Machine)指的是支持向量机,是常见的一种判别方法.在机器学习领域,是一个有监督 ...
- 机器学习之支持向量机—SVM原理代码实现
支持向量机—SVM原理代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/9596898.html 1. 解决 ...
- 机器学习算法 - 支持向量机SVM
在上两节中,我们讲解了机器学习的决策树和k-近邻算法,本节我们讲解另外一种分类算法:支持向量机SVM. SVM是迄今为止最好使用的分类器之一,它可以不加修改即可直接使用,从而得到低错误率的结果. [案 ...
- 【机器学习】支持向量机SVM
关于支持向量机SVM,这里也只是简单地作个要点梳理,尤其是要注意的是SVM的SMO优化算法.核函数的选择以及参数调整.在此不作过多阐述,单从应用层面来讲,重点在于如何使用libsvm,但对其原理算法要 ...
- python机器学习之支持向量机SVM
支持向量机SVM(Support Vector Machine) 关注公众号"轻松学编程"了解更多. [关键词]支持向量,最大几何间隔,拉格朗日乘子法 一.支持向量机的原理 Sup ...
- 机器学习:支持向量机(SVM)
SVM,称为支持向量机,曾经一度是应用最广泛的模型,它有很好的数学基础和理论基础,但是它的数学基础却比以前讲过的那些学习模型复杂很多,我一直认为它是最难推导,比神经网络的BP算法还要难懂,要想完全懂这 ...
- 机器学习-5 支持向量机SVM
一.概念和背景 SVM:Support Vector Machine 支持向量机. 最早是由Vladimir N. Vapnik和Alexey Ya. Chervonenkis在1963年提出的. 目 ...
- 吴裕雄--天生自然python机器学习:支持向量机SVM
基于最大间隔分隔数据 import matplotlib import matplotlib.pyplot as plt from numpy import * xcord0 = [] ycord0 ...
- 机器学习模型-支持向量机(SVM)
二.代码实现 import numpy as np from sklearn import datasets from sklearn.model_selection import train_tes ...
随机推荐
- pyCrypto python 3.5--转
原文地址:https://gxnotes.com/article/198426.html 问题描述 我发现一些PyCrypto安装程序为Python 3.3和3.4,但没有任何Python 3.5. ...
- JS实现掷骰子
JS实现掷骰子 实现方法: 方法一:通过background-position.background-image.backg-repeat三个属性以及jquery animate()方法改变背景骰子图 ...
- CentOS 5/6 下添加epel源
如果既想获得 RHEL 的高质量.高性能.高可靠性,又需要方便易用(关键是免费)的软件包更新功能,那么 Fedora Project 推出的 EPEL(Extra Packages for Enter ...
- 利用Windows2003 IP安全策略实现服务器远程桌面端口(3389)访问控制
1 开始 → 运行 → 对话框中输入gpedit.msc → 确定 2 打开“组策略编辑器” 计算机配置 → Windows配置 → 右键点击“IP安全策略,在 本地计算机” →选择“创建IP安全策略 ...
- ZBrush中Tool工具的保存
ZBrush软件的界面及操作方法与其他的三维软件完全不同,很多初学者常常会觉得有些困难,接下来我们就讲解一下ZBrush®最为基础的操作-Tool工具的保存. 首先要明白什么是Tool工具?我们创建的 ...
- Hihocoder1350-Binary Watch
时间限制:10000ms单点时限:1000ms内存限制:256MB 描述 Consider a binary watch with 5 binary digits to display hours ( ...
- D. Destruction of a Tree_dfs序_性质分析_思维题
题意: 给定一棵树,每次可以拆掉一个树上度数为偶数的点,拆掉该点后,与该点所连的所有边都会被删掉.问,是否有一种删点顺序可以删掉所有的点.如果有,则输出任意一组解. 数据范围:线性做法 O(n)O(n ...
- 【Django】遇到的问题
目前的Django版本是Django version 2.0.4 Python使用的版本是Python 3.6.4 以下会将遇到的问题和各种报错信息记录 报错信息:NameError: name 'u ...
- TensorFlow+实战Google深度学习框架学习笔记(5)----神经网络训练步骤
一.TensorFlow实战Google深度学习框架学习 1.步骤: 1.定义神经网络的结构和前向传播的输出结果. 2.定义损失函数以及选择反向传播优化的算法. 3.生成会话(session)并且在训 ...
- mount --bind
[root@iZwz9i55e7v33yn8ksnh8nZ ~]# mkdir /tmp/dir1 [root@iZwz9i55e7v33yn8ksnh8nZ ~]# mkdir /tmp/dir2 ...
