[poj 2480] Longge's problem 解题报告 （欧拉函数）

题目链接:http://poj.org/problem?id=2480

题目大意：

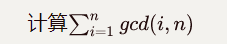
题解：

我一直很欣赏数学题完美的复杂度

#include<cstring>
#include<algorithm>
#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;

const int N=(<<)+;
ll n;
int main()
{
    //printf("%lld\n",phi(3));
    while (scanf("%lld",&n)!=EOF)
    {
        ll ans=n;
        for (ll i=;i*i<=n;i++)
        {
            if (n%i) continue;
            //if (i==1) ans++;
            ll j=;
            while (n%i==) n/=i,j++;
            ans/=i;
            ans*=(i-)*j+i;
        }
        if (n>)
        {
            ans/=n;
            ans*=*n-;
        }
        printf("%lld\n",ans);
    }
    return ;
}