数据结构和算法总结（三）：A* 寻路算法

前言

复习下寻路相关的东西，而且A star寻路在游戏开发中应用挺多的，故记录下。

正文

迪杰斯特拉算法

说起A*得先谈谈Dijkstra算法，它是在BFS基础上的一种带权值的两点最短寻路贪心算法。

算法步骤

0.初始化图，输入起点，将所有点到起始点的距离设置为∞。

1.将起始点OriginNode记录为已访问，并从OriginNode开始将周围的点加入到待遍历列表中，更新到达这些点的距离，并将他们的父节点设置为起始点OriginNode。

2.如果待遍历列表不为空，则从列表中取出到达距离最小的点currentNode；反之则跳到第5步。

3.遍历currentNode邻接的点neighbors:

1）  如果已访问过，则遍历其他点。

2） 如果邻接的某点neighbor已经在待遍历列表中，则比较neighbor当前的距离distance(OriginNode,neighbor) 与  distance(OriginNode,currentNode) + distance(currentNode,neighbor), 如果后者更小，则将neighbor的距离值更新为该值并将父节点设置为currentNode。

3） 如果不在待遍历列表，则将neighbor放入待遍历列表，并则将neighbor的距离值更新为  distance(OriginNode,currentNode) + distance(currentNode,neighbor), 并将父节点设置为currentNode。

4.重复第2步

5.输入终点，从终点开始回溯父节点，打印路径。

动态过程

A* 寻路算法

A*的思路其实与Dijkstra一致，相比较Dijkstra，A*引入了一个启发公式来衡量消耗

其中 g(n) 代表从起始点到当前点的消耗，h(n) 代表终点到当前点的预估消耗（通常用曼哈顿距离或者欧拉距离衡量，这里不赘述，参考）。

算法思路

/*
A*寻路算法
 
   带权值的BFS
   每个点保存达到该点的消耗F = G值（出发点到当前点的代价值） + H值（目标点到当前点的预估距离，常用曼哈顿距离或者欧拉距离）
   维护着两个列表，开放列表和关闭列表
 
   逻辑:
   初始化列表Close,Open,Path,将StartNode放入Open列表中
   while(true)
   {
       从Open表中取得F值最小的节点CurrentNode.
       从Open表中删除CurrentNode
       将CurrentNode加入Close表中
       if ( CurrentNode 是 目标点targetNode)
       {
           从CurrentNode点回溯直到起点并将所有回溯的节点加入Path表
           打印Path表
           return;
       }
       for (CurrentNode 的每一个邻接点 neighbor)
       {
           if(neighbor 在 Close表中 || neighbor 不可通行)
           {
               continue;
           }
           if(neighbor 在 Open表中)
           {
               if( CurrentNode 到达neighbor的消耗costG + node的G值 < neighbor的G值)
               {
                   更新neighbor的G值;
                   将neighbor的回溯节点fatherNode设置为CurrentNode;
               }
           }
           else
           {
               更新neighbor的G值;
               更新neighbor的H值;
               将neighbor的回溯节点fatherNode设置为CurrentNode;
               将neighbor放入Open列表;
           }
       }
   }
 */

动态过程

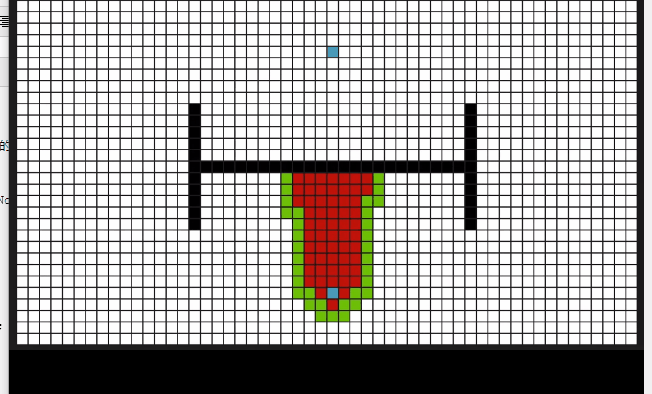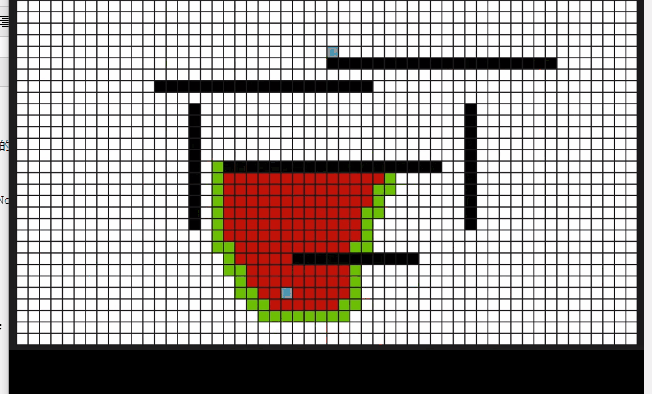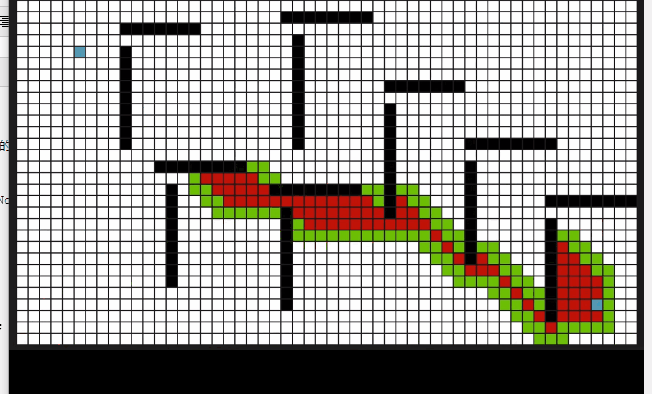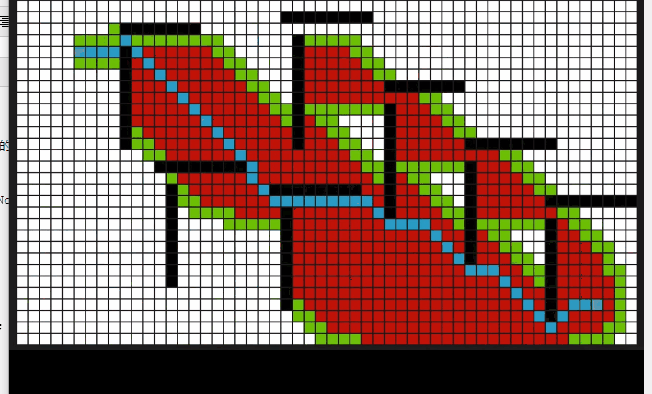
代码:

AstarNode的定义实现.

Astar.h

#pragma once
#include <vector>
#include <math.h>
 
using std::vector;
 
class AstarNode
{
private:
    int m_igValue;
    int m_ihValue;
    int m_ifValue;
    AstarNode* m_father;
public:
    int x;
    int y;
    bool isPass;
public:
    void   SetG(int iValue);
    int    GetG() const;
    int    GetH() const;
    int    GetF() const;
    void   CalculateH(const AstarNode* endNode);
    void   SetFather(AstarNode* node);
    AstarNode*   GetFather() const;
    bool isInList(const vector<AstarNode*>& nodeList) const;
public:
    AstarNode();
    AstarNode(int x,int y);
    AstarNode(const AstarNode& node);
    ~AstarNode();
    AstarNode& operator=(const AstarNode& node);
};

Astar.cpp

#include "Astar.h"
 
AstarNode::AstarNode()
{
    isPass = true;
    m_igValue = 0;
    m_ihValue = 0;
    m_ifValue = 0;
    m_father = nullptr;
}
 
AstarNode::AstarNode(int x,int y)
{
    isPass = true;
    m_igValue = 0;
    m_ihValue = 0;
    m_ifValue = 0;
    m_father = nullptr;
    this->x = x;
    this->y = y;
}
 
AstarNode::AstarNode(const AstarNode& node)
{
    isPass = node.isPass;
    m_igValue = node.GetG();
    m_ihValue = node.GetH();
    m_ifValue = node.GetF();
    m_father = node.GetFather();
    this->x = node.x;
    this->y = node.y;
}
 
AstarNode& AstarNode::operator=(const AstarNode& node)
 {
    isPass = node.isPass;
    m_igValue = node.GetG();
    m_ihValue = node.GetH();
    m_ifValue = node.GetF();
    m_father = node.GetFather();
    this->x = node.x;
    this->y = node.y;
    return *this;
 }
 
AstarNode::~AstarNode()
{
 
}
 
void AstarNode::SetG(int iValue)
{
    m_igValue = iValue;
}
 
int AstarNode::GetG() const
{
    return m_igValue;
}
 
int AstarNode::GetF() const
{
    return m_igValue + m_ihValue;
}
 
int AstarNode::GetH() const
{
    return m_ihValue;
}
 
void AstarNode::CalculateH(const AstarNode* endNode)
{
    m_ihValue = abs(endNode->x - x) + abs(endNode->y - y);
}
 
void AstarNode::SetFather(AstarNode* node)
{
    m_father = node;
}
 
AstarNode* AstarNode::GetFather() const
{
    return m_father;
}
 
bool AstarNode::isInList(const vector<AstarNode*>& nodeList) const
{
    for(auto iter = nodeList.begin();iter != nodeList.end();iter++)
    {
        if((*iter)->x == this->x && (*iter)->y == this->y)
              return true;
    }
    return false;
}

main.cpp

#include "Astar.cpp"
#include <algorithm>
using namespace std;
 
/*
   'e' 终点
   's' 起点
   '#' 障碍物
   '-' 可通行点
   'o' 回溯路径节点
*/
 
vector<vector<char>> graph = {
    {'-', '-', '-', '-', '-', '-', '-'},
    {'-', '-', 'e', '#', '-', '-', '-'},
    {'-', '#', '#', '#', '#', '-', '-'},
    {'-', '-', '-', '-', '#', '#', '-'},
    {'-', '-', '#', '-', '#', '-', '-'},
    {'-', '-', '-', '#', '-', '-', '-'},
    {'-', '-', '-', '-', '-', '-', 's'},
};
 
void BuildGraph(vector<vector<AstarNode *>> &astarGraph, AstarNode &start, AstarNode &end)
{
    for (int i = 0; i < astarGraph.size(); i++)
    {
        auto row = astarGraph[i];
        for (int j = 0; j < row.size(); j++)
        {
            char mark = graph[i][j];
            if (mark == 's')
            {
                start.x = i;
                start.y = j;
                start.SetG(0);
                start.CalculateH(&end);
                astarGraph[i][j] = &start;
            }
            else if (mark == 'e')
            {
                end.x = i;
                end.y = j;
                astarGraph[i][j] = &end;
            }
            else if (mark == '#')
            {
                astarGraph[i][j] = new AstarNode(i, j);
                astarGraph[i][j]->isPass = false;
            }
            else
            {
                astarGraph[i][j] = new AstarNode(i, j);
            }
        }
    }
}
 
void printGraph()
{
    for (int i = 0; i < graph.size(); i++)
    {
        auto line = graph[i];
        for (int j = 0; j < line.size(); j++)
        {
            cout << line[j] << " ";
        }
        cout << endl;
    }
}
 
vector<AstarNode *>::iterator GetMinFNode(vector<AstarNode *> &openList)
{
    auto tmp = openList.begin();
    for (auto iter = openList.begin(); iter != openList.end(); iter++)
    {
        if ((*iter)->GetF() < (*tmp)->GetF())
        {
            tmp = iter;
        }
    }
    return tmp;
}
 
inline int GetCost(int xDiff, int yDiff)
{
    if (xDiff == 0 || yDiff == 0)
        return 10;
    return 14;
}
 
void SearchOneNode(AstarNode &currentNode, AstarNode &neighbor, AstarNode &startNode, AstarNode &endNode, vector<AstarNode *> &openList, vector<AstarNode *> &closeList)
{
    if (neighbor.isInList(closeList) || !neighbor.isPass)
        return;
    int gCost = GetCost(currentNode.x - neighbor.x, currentNode.y - neighbor.y);
    if (neighbor.isInList(openList))
    {
        if (currentNode.GetG() + gCost < neighbor.GetG())
        {
            neighbor.SetG(currentNode.GetG() + gCost);
            neighbor.SetFather(&currentNode);
        }
    }
    else
    {
        neighbor.SetG(currentNode.GetG() + gCost);
        neighbor.SetFather(&currentNode);
        neighbor.CalculateH(&endNode);
        openList.push_back(&neighbor);
    }
}
 
void Astar()
{
    vector<AstarNode *> OpenList;
    vector<AstarNode *> CloseList;
    vector<AstarNode *> Path;
    size_t len = graph.size();
    vector<vector<AstarNode *>> astarGraph(len, vector<AstarNode *>(len));
 
    AstarNode startNode;
    AstarNode endNode;
 
    BuildGraph(astarGraph, startNode, endNode);
    OpenList.push_back(&startNode);
    while (!OpenList.empty())
    {
        auto it = GetMinFNode(OpenList);
        AstarNode *currentNode = *it;
        OpenList.erase(it);
        CloseList.push_back(currentNode);
        if (currentNode->x == endNode.x && currentNode->y == endNode.y)
        {
            while (currentNode->GetFather())
            {
                graph[currentNode->x][currentNode->y] = graph[currentNode->x][currentNode->y] == '-' ? 'o' : 'e';
                Path.push_back(currentNode);
                currentNode = currentNode->GetFather();
            }
            printGraph();
            break;
        }
        int curX = currentNode->x;
        int curY = currentNode->y;
        int row = graph.size();
        int column = row;
        if (curX + 1 < row)
            SearchOneNode(*currentNode, *astarGraph[curX + 1][curY], startNode, endNode, OpenList, CloseList);
        if (curX - 1 >= 0)
            SearchOneNode(*currentNode, *astarGraph[curX - 1][curY], startNode, endNode, OpenList, CloseList);
        if (curY + 1 < column)
            SearchOneNode(*currentNode, *astarGraph[curX][curY + 1], startNode, endNode, OpenList, CloseList);
        if (curY - 1 >= 0)
            SearchOneNode(*currentNode, *astarGraph[curX][curY - 1], startNode, endNode, OpenList, CloseList);
        if (curX - 1 >= 0 && curY - 1 >= 0)
            SearchOneNode(*currentNode, *astarGraph[curX - 1][curY - 1], startNode, endNode, OpenList, CloseList);
        if (curX - 1 >= 0 && curY + 1 < column)
            SearchOneNode(*currentNode, *astarGraph[curX - 1][curY + 1], startNode, endNode, OpenList, CloseList);
        if (curX + 1 < row && curY - 1 >= 0)
            SearchOneNode(*currentNode, *astarGraph[curX + 1][curY - 1], startNode, endNode, OpenList, CloseList);
        if (curX + 1 < row && curY + 1 < row)
            SearchOneNode(*currentNode, *astarGraph[curX + 1][curY + 1], startNode, endNode, OpenList, CloseList);
    }
    cout << endl;
}
 
int main()
{
    auto start = chrono::steady_clock::now();
    Astar();
    auto end = chrono::steady_clock::now();
    cout << chrono::duration<double, milli>(end - start).count() << " ms" << endl;
    getchar();
}

参考资料

欧式距离与曼哈顿距离       作者:大鱼-瓶邪

A* 搜索算法（Python ）     作者: 漫步_9378

A* Pathfinding (需要梯子)   作者: Sebastian Lague

 

 

VisualGO 算法可视化