[Tarjan系列] Tarjan算法求无向图的桥和割点

RobertTarjan真的是一个传说级的大人物。

他发明的LCT，SplayTree这些数据结构真的给我带来了诸多便利，各种动态图论题都可以用LCT解决。

而且，Tarjan并不只发明了LCT，他对计算机科学做出的贡献真的很多。

这一篇我就来以他名字命名的Tarjan算法可以O(n)求出无向图的割点和桥。

进一步可以求出无向图的DCC( 双连通分量 )。不止无向图，Tarjan算法还可以求出有向图的SCC( 强连通分量 )。

Tarjan算法基于dfs，接下来我们引入几个基本概念。

dfn：时间戳

我们对一张图进行深度优先遍历，根据第一次访问到它的时间顺序给它打上一个标记，这个标记就是时间戳。

搜索树：

在一张无向连通图中选定任意一个节点进行深度优先遍历，每个点仅访问一次。所有发生了递归的边会构成一棵树，我们称其为无向连通图的“搜索树”。

追溯值：

除了时间戳，Tarjan算法还引入了另一个概念：“追溯值” low。

我们用subtree(x)表示搜索树中以x为根的子树，low[x]定义为下列节点的时间戳的最小值：

1. subtree(x)中的节点 2. 通过一条不在搜索树上的边，能够到达subtree(x)中的节点

我们来画一个图理解一下：（方便起见，图中的节点编号就是它的时间戳）

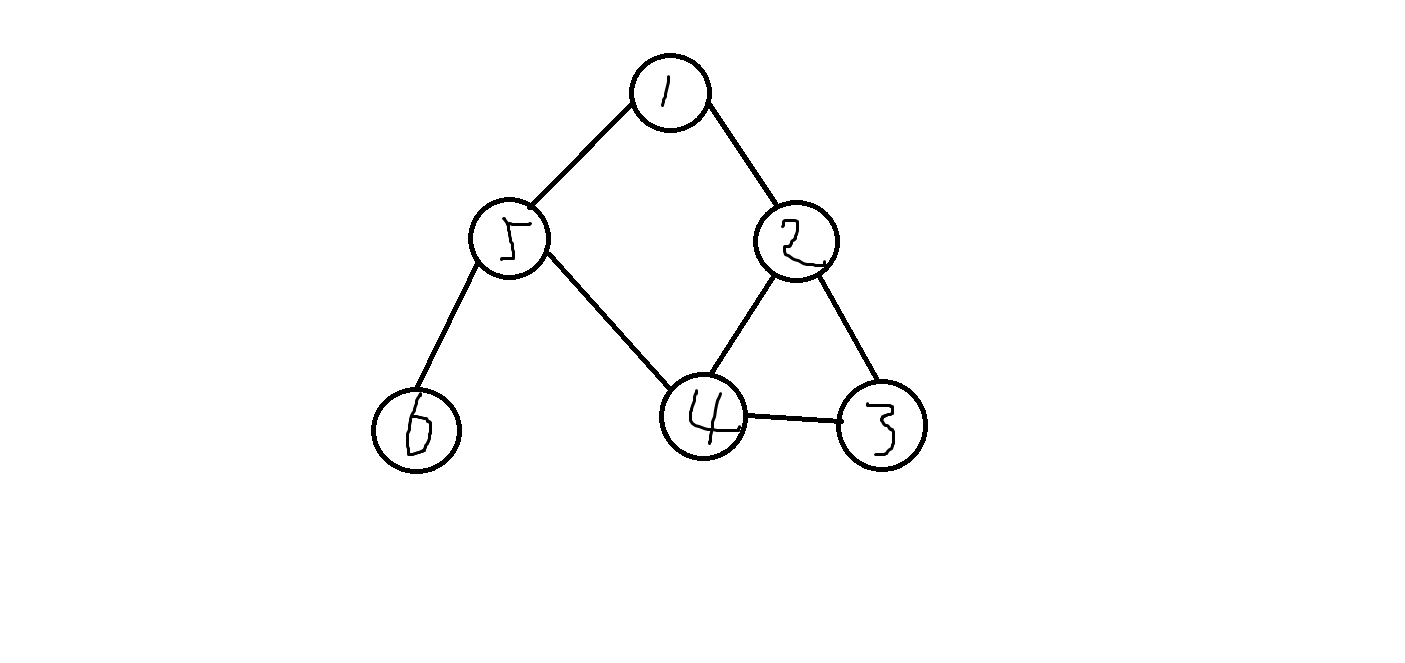
图中红色的边就是这张图的搜索树

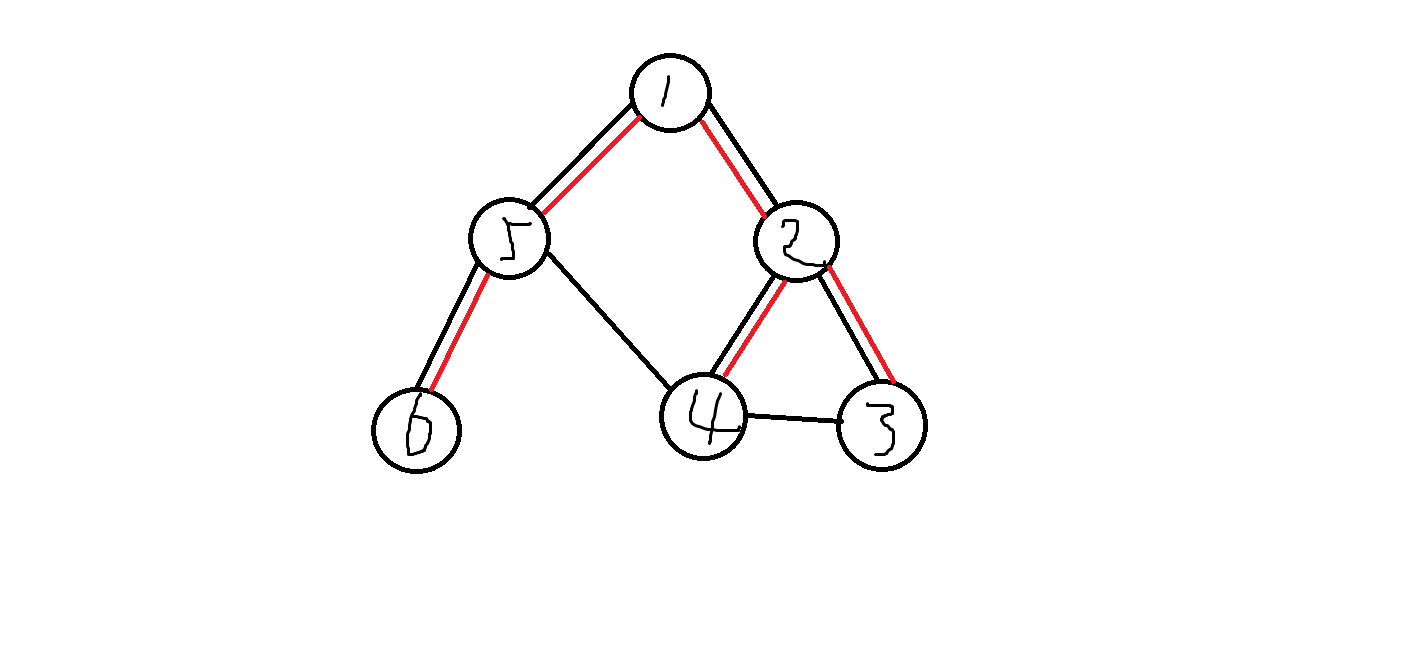
那么我们容易得出：subtree(2)={4,3},5可以通过不在搜索树上的边到达subtree(2)。

所以，low[2]=min{dfn[4],dfn[3],dfn[5]}，得出low[2]=3。

根据定义来计算low[x]的方法就非常明显了。因为subtree(x)包括x，所以先令low[x]=dfn[x]。

然后遍历从x出发的每一条边(x,y)，计算low[x]。

接下来给出无向图的桥和割点判定法则。

无向边(x,y)是桥，当且仅当x在搜索树上的一个子节点y满足low[y]>dfn[x]。

若x不是搜索树的根节点，则x是割点当且仅当搜索树上的一个子节点y满足low[y]>=dfn[x]。

若x是根节点，则x是割点当且仅当搜索树上存在至少两个x的子节点y1,y2满足上式。

桥边有以下性质：

1. 桥一定是搜索树中的边 2. 一个简单环中边都不是桥边

一个环被称为简单环当且仅当其包含的所有点都只在这个环中被经过了一次。

扩展内容：这里给出用dfs求出一个图中所有简单环的代码

int cnt;
void dfs(int u){
    dfn[u]=++cnt;
    for(int i=head[u];i;i=nxt(i)){
        int v=to(i);
        if(v==fa[u])continue;
        if(!dfn[v])fa[v]=u,dfs(v);
        else if(dfn[u]<dfn[v]){
            printf("%d",v);
            do{
                printf(" %d",fa[v]);v=fa[v];
            }while(v!=u);
            //找完一个环了
            putchar('\n');
        }
    }
}

这个作为扩展内容就不再展开叙述。

下面给出求出无向图中所有的桥的代码：

#include<bits/stdc++.h>
#define N 100010
using namespace std;
inline int read(){
    int data=,w=;char ch=;
    while(ch!='-' && (ch<''||ch>''))ch=getchar();
    if(ch=='-')w=-,ch=getchar();
    while(ch>='' && ch<='')data=data*+ch-'',ch=getchar();
    return data*w;
}
struct Edge{
    int nxt,to;
    #define nxt(x) e[x].nxt
    #define to(x) e[x].to
}e[N<<];
int dfn[N],low[N],tot=;//储存边的编号，由于要用^1找反向边，从1开始
int bridge[N],head[N];
int n,m,cnt;
void addedge(int f,int t){
    nxt(++tot)=head[f];to(tot)=t;head[f]=tot;
}
void tarjan(int x,int in_edge){//in_edge表示递归进入每个节点的边的编号
    dfn[x]=low[x]=++cnt;
    for(int i=head[x];i;i=nxt(i)){
        int y=to(i);
        if(!dfn[y]){
            tarjan(y,i);
            low[x]=min(low[x],low[y]);//在搜索树上的边
            if(low[y]>dfn[x])//桥判定法则
                bridge[i]=bridge[i^]=;//这条边和它的反向边都是桥
        }else if(i!=(in_edge^))
            low[x]=min(low[x],dfn[y]);//不在搜索树上的边
    }
}
int main(){
    n=read();m=read();
    for(int i=;i<=m;i++){
        int x=read(),y=read();
        addedge(x,y);addedge(y,x);
    }
    for(int i=;i<=n;i++)
        if(!dfn[i])tarjan(i,);
    for(int i=;i<tot;i+=)
        if(bridge[i])
            printf("%d %d\n",to(i^),to(i));//输出桥两边的点
}

以上就是求无向图中所有桥的程序了，可以自己画图模拟一下tarjan算法的流程加深理解。

下面给出求无向图中所有割点的程序：

这里需要注意的是，由于割点判定法则是小于等于号，所以不需要考虑父节点和重边的问题，所有dfn[x]都可以用来更新low[x]

#include<bits/stdc++.h>
#define N 100010
using namespace std;
inline int read(){
    int data=,w=;char ch=;
    while(ch!='-' && (ch<''||ch>''))ch=getchar();
    if(ch=='-')w=-,ch=getchar();
    while(ch>='' && ch<='')data=data*+ch-'',ch=getchar();
    return data*w;
}
struct Edge{
    int nxt,to;
    #define nxt(x) e[x].nxt
    #define to(x) e[x].to
}e[N<<];
int head[N],dfn[N],low[N],rt,tot=,n,m,cnt;
int cut[N];
inline void addedge(int f,int t){
    nxt(++tot)=head[f];to(tot)=t;head[f]=tot;
}
void tarjan(int x){
    dfn[x]=low[x]=++cnt;
    int flag=;
    for(int i=head[x];i;i=nxt(i)){
        int y=to(i);
        if(!dfn[y]){
            tarjan(y);
            low[x]=min(low[x],low[y]);
            if(low[y]>=dfn[x]){//就一个割点判断法则没必要解释什么了吧？
                flag++;
                if(x!=rt||flag>)cut[x]=;
            }
        }else low[x]=min(low[x],dfn[y]);
    }
}
int main(){
    n=read();m=read();
    for(int i=;i<=m;i++){
        int x=read(),y=read();
        if(x==y)continue; //自环直接判掉好吧，不多bb
        addedge(x,y);addedge(y,x);
    }
    for(int i=;i<=n;i++)
        if(!dfn[i])rt=i,tarjan(i);//无向图不一定连通，对每一个连通块都要跑一发tarjan
    for(int i=;i<=n;i++)
        if(cut[i])printf("%d ",i);
    return ;
}

桥边判定法则和割点判定法则后面会update上，这一篇暂时更到这里，下一篇讲e-DCC和v-DCC的求法

主要是联赛在即，更新尽量多的算法扎实自己基础才要紧些...请多见谅