Noip2013(普及组) 车站分级

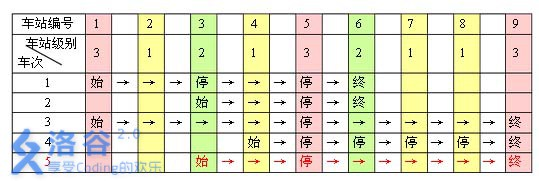
题目描述

一条单向的铁路线上，依次有编号为 , , …, n 的 n 个火车站。每个火车站都有一个级别，最低为  级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是  趟车次的运行情况。其中，前  趟车次均满足要求，而第  趟车次由于停靠了  号火车站（ 级）却未停靠途经的  号火车站（亦为  级）而不满足要求。

现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：
输入文件为 level.in。

第一行包含  个正整数 n, m，用一个空格隔开。

第 i +  行（ ≤ i ≤ m）中，首先是一个正整数 si（ ≤ si ≤ n），表示第 i 趟车次有 si 个停靠站；接下来有 si个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：
输出文件为 level.out。

输出只有一行，包含一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入样例#：

输出样例#：

输入样例#：

输出样例#：

说明

对于 %的数据， ≤ n, m ≤ ；

对于 %的数据， ≤ n, m ≤ ；

对于 %的数据， ≤ n, m ≤ 。

题目

芒果君：拓扑排序还是很容易看出来的（毕竟好多奇奇怪怪的题最后都变成图论了……），关系也很好建立，被跳过的站点比没跳过的优先级低，那就暴力建边。之前求拓扑排序都是栈模拟，这次没换dfs之前T了3个点。以后就都用dfs了。

#include<cstdio>
#include<cmath>
#include<ctime>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<vector>
#define maxn 1010
#define inf 1<<29
using namespace std;
typedef long long ll;
vector<int>Edge[maxn];
stack<int>S;
int ans,n,m,st,ed,rm,num,rec[maxn],tmp[maxn];
bool vis[maxn][maxn];
inline int read()
{
    char ch=getchar();
    int x();
    while(ch<''||ch>'') ch=getchar();
    while(ch>=''&&ch<=''){
        x=x*+ch-'';
        ch=getchar();
    }
    return x;
}
void dfs(int x)
{
    if(rec[x]) return;
    rec[x]=;
    for(int i=;i<Edge[x].size();++i){
        dfs(Edge[x][i]);
        rec[x]=max(rec[x],rec[Edge[x][i]]+);
    }
    ans=max(ans,rec[x]);
}
int main()
{
    scanf("%d%d",&n,&m);
    rm=n;
    while(m--){
        num=read();
        for(int i=;i<=num;++i) tmp[i]=read();
        for(int i=;i<num;++i) for(int j=tmp[i]+;j<tmp[i+];++j) for(int k=;k<=num;++k) if(!vis[j][tmp[k]]) Edge[j].push_back(tmp[k]),vis[j][tmp[k]]=;
    }
    for(int i=;i<=n;++i) if(!rec[i]) dfs(i);
    printf("%d\n",ans);
    return ;
}