Leetcode之广度优先搜索（BFS）专题-994. 腐烂的橘子（Rotting Oranges）

Leetcode之广度优先搜索（BFS）专题-994. 腐烂的橘子（Rotting Oranges）

BFS入门详解：Leetcode之广度优先搜索（BFS）专题-429. N叉树的层序遍历（N-ary Tree Level Order Traversal）

---

在给定的网格中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，任何与腐烂的橘子（在 4 个正方向上）相邻的新鲜橘子都会腐烂。

返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1。

示例 1：

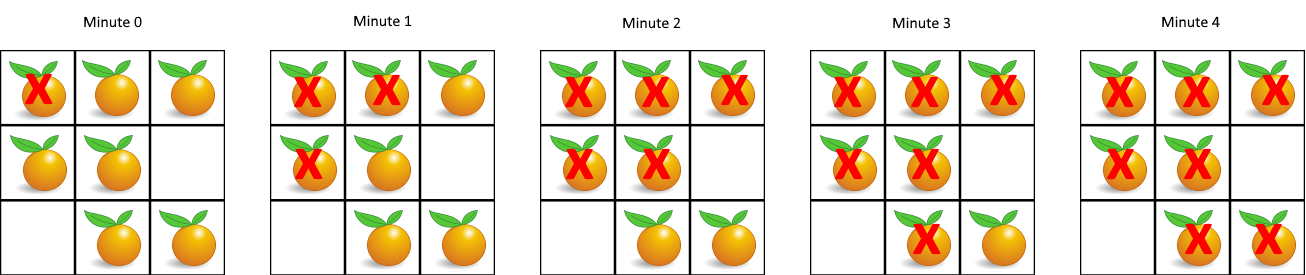
输入：[[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：[[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个正向上。

示例 3：

输入：[[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

1. 1 <= grid.length <= 10
2. 1 <= grid[0].length <= 10
3. grid[i][j] 仅为 0、1 或 2

---

把所有烂的橘子压进队列，然后每次把烂橘子周围的好橘子变成坏橘子，然后时间多1，就可以了。

class Solution {
    int dirx[] = {1,-1,0,0};
    int diry[] = {0,0,1,-1};
    private static class POINT{
        int x,y;
        int t = 0;
        public POINT(int x,int y,int t){
            this.x = x;
            this.y = y;
            this.t = t;
        }
    }

    public int orangesRotting(int[][] grid) {
        int ans = 0;
        Queue<POINT> queue = new LinkedList<>();
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if(grid[i][j]==2){
                    queue.offer(new POINT(i,j,0));
                }
            }
        }

        while (!queue.isEmpty()){
            POINT temp = queue.poll();
            int x = temp.x;
            int y = temp.y;
            int t = temp.t;
            ans = Math.max(ans, t);
            for (int i = 0; i < 4; i++) {
                int xx = x + dirx[i];
                int yy = y + diry[i];
                if(xx>=0 && yy>=0 && xx<grid.length && yy<grid[0].length && grid[xx][yy]==1){
                    grid[xx][yy] = 2;
                    queue.offer(new POINT(xx,yy,t+1));
                }
            }
        }

        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[0].length; j++) {
                if(grid[i][j]==1){
                    return -1;
                }
            }
        }
        return ans;
    }
}