leetcode 1266. Minimum Time Visiting All Points

On a plane there are n points with integer coordinates points[i] = [xi, yi]. Your task is to find the minimum time in seconds to visit all points.

You can move according to the next rules:

• In one second always you can either move vertically, horizontally by one unit or diagonally (it means to move one unit vertically and one unit horizontally in one second).
• You have to visit the points in the same order as they appear in the array.

Example 1:

Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
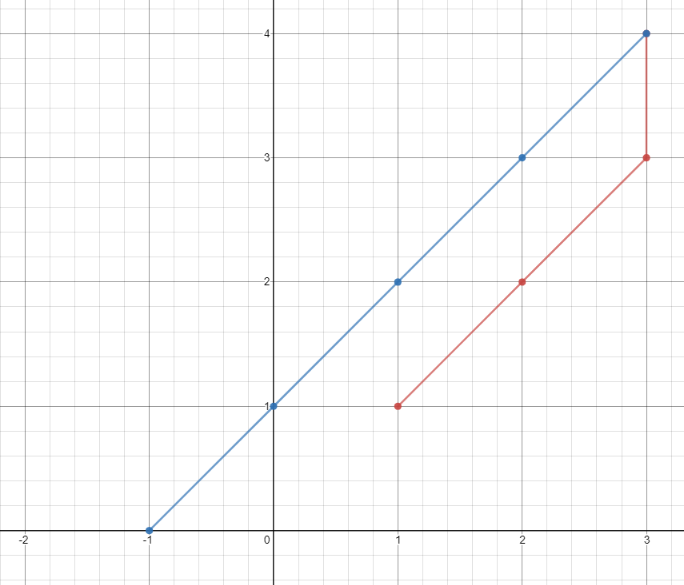
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
Time from [1,1] to [3,4] = 3 seconds
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds

Example 2:

Input: points = [[3,2],[-2,2]]
Output: 5

Constraints:

• points.length == n
• 1 <= n <= 100
• points[i].length == 2
• -1000 <= points[i][0], points[i][1] <= 1000

思路：为了计算两个点的最短时间对应的路径，我们应该尽量走对角，比如(1, 1) 到 (3, 4), 通过走对角方式(1, 1) -> (2, 2) -> (3, 3) -> (3, 4), 不能直接从（1, 1）到 (3, 4), 会先走3对角，在往垂直方向1。

针对(x1, y1) -> (x2, y2), 水平方向 |x2 - x1|, 垂直方向|y2 - y1|, 走对角 min(|x2 - x1|, |y2 - y1|), 走水平或垂直max(|x2 - x1|, |y2 - y1|) - min(|x2 - x1|, |y2 - y1|), 加起来为max(|x2 - x1|, |y2 - y1|,

根据题意，可以直接贪心思想，求出相邻两点的时间，并累加。

 class Solution {
 public:
     int minTimeToVisitAllPoints(vector<vector<int>>& points) {
         int cnt = ;
         for (int i = ; i < points.size(); ++i) {
             cnt += max(abs(points[i][] - points[i - ][]), abs(points[i][] - points[i - ][]));
         }
         return cnt;
     }
 };