2019.6.20 校内测试 NOIP模拟 Day 1 分析+题解

这次是zay神仙给我们出的NOIP模拟题，不得不说好难啊QwQ，又倒数了~

T1 大美江湖

这个题是一个简单的模拟题。   ----zay

唯一的坑点就是打怪的时候计算向上取整时，如果用ceil函数一定要先转化成double类型（话说我就这么掉坑里了？QwQ）

测试点 1： 0 次询问，所以直接freopen一下输出文件即可得分。期望得分 10 分。

测试点 4、5： 由于保证人物不移动，而且不捡拾出生点的物资也不在出生点打怪，所以攻击 防御一定全部为初始值，耗血一定为 0 ，直接输出 q 行数据即可。期望得分 20 分。

测试点 6、7、8： 地图上没有怪物，就不需要计算耗血那个复杂的式子，直接累加获得的药水即 可。期望得分 30 分。

测试点2、3、9、10： 考虑暴力模拟每一次行走，耗血的式子是可以 O(1) 计算的，而累加攻击防御 也是 O(1) 的，于是总复杂地 O(q)，可以通过本题。期望得分 40 分。 需要注意的是在计算耗血的时候需要用到取整函数。如果使用 cpp 的 cmath 库里面的 ceil() 函数的话，需要注意括号里相除两数不能全为 int。

标程代码：

#include <cmath>
#include <cstdio>
#include <algorithm>

const int maxn = ;

char mp[maxn][maxn];

int n, m, px, py, q;

struct Character {
  int HP, ST, DE;
  int ehp, est, ede;

  void print() {
    printf("%d %d %d\n", this->HP, this->ST, this->DE);
  }

  void fight() {
    int x = int(ceil(1.0 * ehp / std::max(, ST - ede)));
    this->HP += std::max(, x * std::max(, est - DE));
  }

  void update(const char x) {
    switch (x) {
      case 'R': {
        this->HP = std::max(, this->HP - );
        break;
      }
      case 'Q': {
        this->ST += ;
        break;
      }
      case 'Y': {
        this->DE += ;
        break;
      }
      case 'M': {
        fight();
        break;
      }
    }
  }
};
Character my;

void mov(const int x);

int main() {
  freopen("mzq.in", "r", stdin);
  freopen("mzq.out", "w", stdout);
  scanf("%d%d", &n, &m);
  for (int i = ; i <= n; ++i) {
    scanf("%s", mp[i] + );
  }
  scanf("%d%d%d", &my.ehp, &my.est, &my.ede);
  scanf("%d%d", &px, &py);
  scanf("%d%d", &my.ST, &my.DE);
  scanf("%d", &q);
  int x;
  while (q--) {

    scanf("%d", &x);
    if (x == ) {
      my.print();
    } else {
      x = ;
      scanf("%d", &x);
      mov(x);
    }
  }
  return ;
}

void mov(const int x) {
  switch (x) {
    case : {
      --py;
      break;
    }
    case : {
      ++py;
      break;
    }
    case : {
      --px;
      break;
    }
    case : {
      ++px;
      break;
    }
    default: {
      puts("I AK IOI");
      break;
    }
  };
  my.update(mp[px][py]);
}

我改完之后的代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n,m,hp_e,st_e,de_e,st_m,de_m,hp_m;
int x,y,q,cz,where;            //从(x,y)开始走
char a[][];
int fight()
{
    int ans=ceil(1.0*hp_e/(max(,st_m-de_e)));   //注意先转化成double类型
    return max(,(int)ans*max(,st_e-de_m));
}
int main()
{
    freopen("mzq.in","r",stdin);
    freopen("mzq.out","w",stdout);
    n=read();m=read();
    for(int i=;i<=n;i++)
       for(int j=;j<=m;j++)
          cin>>a[i][j];     //地图
    hp_e=read();
    st_e=read();
    de_e=read();
    x=read();y=read();     //从(x,y)开始走
    st_m=read();
    de_m=read();
    q=read();
    for(int i=;i<=q;i++)
    {
        cz=read();
        if(cz==)        //查询
          printf("%d %d %d\n",hp_m,st_m,de_m);
        else             //移动
        {
            where=read();
            if(where==) y--;     //向左走
            if(where==) y++;     //向右走
            if(where==) x--;     //向上走
            if(where==) x++;     //向下走
            if(a[x][y]=='.') continue;
            if(a[x][y]=='R') hp_m-=;  //回血
            if(hp_m<) hp_m=;          //小于10的话回到0
            if(a[x][y]=='Q') st_m+=;   //加5攻击力
            if(a[x][y]=='Y') de_m+=;   //加5防御力
            if(a[x][y]=='M') hp_m+=fight();   //打怪
        }
    }
    return ;
}

T2 腐草为萤

子任务 1： 只有一个点，所以只有 {1} 这一种集合，于是答案为 1。期望得分 5 分。

子任务 2、3： 爆搜，枚举所有可能的集合，然后计算答案。 由于每个点只有选进集合或不选两种可能，所以一共有 2 n 个集合，然后可以 O(n) 的去检验集合是否合法，顺便统计答案。于是总复杂度 O(2 n×n)。期望得分 25分。

子任务 4、5： 考虑 DP。设 fu 是以 u 为根的子树的答案。 如果 u 没有孩子，那么 fu = u^T。 如果 u 只有一个孩子 v，那么要么选 u 不选 u 的子孙，要么不选 u。不选 u 的答案即为 fv，选 u 的答案即为 u ^T。两种情况加起来就是 fu。 如果 u 有两个孩子 x,y。考虑要么选 u，要么只选 x 的子树内的元素，要么 只选 y 的子树内的元素，要么既选 x 内的元素又选 y 内的元素但不选 u。前三种 情况的答案易得。现在考虑第四种情况的答案。设 s 是 x 子树内的某个集合。考 虑无论 y 的子树内怎么选，再加上 s 都是合法的，因为 y 和 x 之间没有祖先后 代关系且 s 在 x 之内。设 gu 是以 u 为根能选择的集合个数，那么一共有 gy 个 集合选择 s 以后依旧合法，设 s 的权值和为 ws，于是 s 的贡献即为 ws×gy。由于 fx 为 x 子树内所有可能集合的权值和，所以可以发现 ∑ws = fx 。于是 x 子树内 的集合对答案的总贡献是 fx×gy。同理，y 子树内的集合对答案的贡献是 fy×gy。 于是 fu=fy×gx+fx×gy+fx+fy+u T。gu=gx×gy+gx+gy+1。时间复杂度O(n)，期望得分 30 分。

子任务6、7： 虑在遍历子节点的时候，已经遍历了一些子节点，现在新加入了一个子节点。 由于新加入一个子节点与之前遍历的子节点没有祖先后代关系，于是可以之前遍历 过得子树看成一棵子树，然后问题就变成了子任务4、5。期望得分 40 分。 需要注意的是由于读入规模达到了10e6左右，需要普通的读入优化。

标程代码：

#include <cstdio>

typedef long long int ll;

const int maxn = ;
const int MOD = ;

template <typename T>
inline void qr(T &x) {
  char ch;
  do { ch = getchar(); } while ((ch > '') || (ch < ''));
  do { x = (x << ) + (x << ) + (ch ^ ); ch = getchar(); } while ((ch >= '') && (ch <= ''));
}

int n, T;
int MU[maxn], frog[maxn], gorf[maxn];
bool vis[maxn];

struct Edge {
  int v;
  Edge *nxt;

  Edge(const int _v, Edge *h) : v(_v), nxt(h) {}
};
Edge *hd[maxn];

void dfs(const int u);

int main() {
  freopen("dzy.in", "r", stdin);
  freopen("dzy.out", "w", stdout);
  qr(n); qr(T);
  if (T) {
    for (int i = ; i <= n; ++i) {
      MU[i] = i;
    }
  } else {
    for (int i = ; i <= n; ++i) {
      MU[i] = ;
    }
  }
  for (int i = , u, v; i < n; ++i) {
    u = v = ; qr(u); qr(v);
    hd[u] = new Edge(v, hd[u]);
    hd[v] = new Edge(u, hd[v]);
  }
  dfs();
  printf("%d\n", frog[] % MOD);
  return ;
}

void dfs(const int u) {
  vis[u] = true;
  for (auto e = hd[u]; e; e = e->nxt) if (!vis[e->v]) {
    int v = e->v;
    dfs(v);
    frog[u] = (frog[u] * (gorf[v] + 1ll) % MOD) + (frog[v] * (gorf[u] + 1ll) % MOD);
    gorf[u] = (gorf[u] + gorf[v] + (1ll * gorf[u] * gorf[v])) % MOD;
  }
  frog[u] = (frog[u] + MU[u]) % MOD;
  ++gorf[u];
}

T3  锦鲤抄

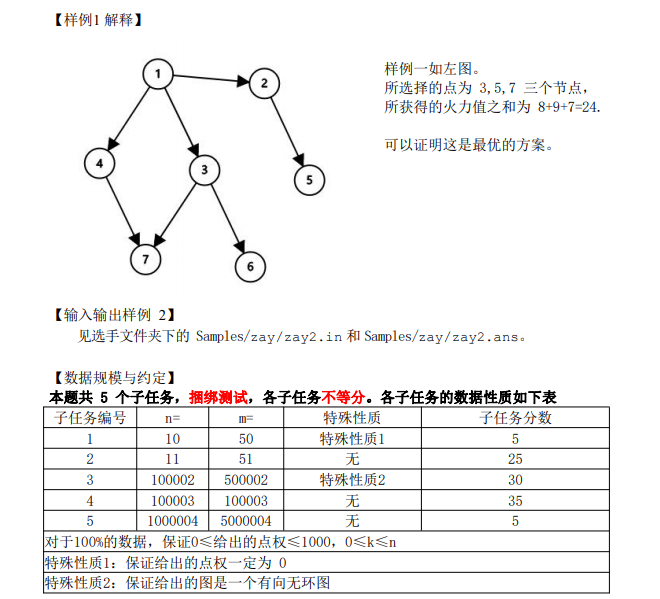
子任务 1： 点权都是0，于是无论怎么选答案都是 0，输出 0 即可。期望得分 5 分。

子任务 2： 爆搜，枚举所有可能的顺序，然后计算答案。 由于保证了数据随机，可以在搜索的过程中进行剪枝，效率很高，期望得分25 分。

子任务 3： 给出的是一个 DAG 。考虑对于一个 DAG 来说，一个良好的的性质就是在拓扑 序后面的点无论如何变化都无法影响到前面的点。这个题也一样。对于任意一个不 出现原图中本身入度为 0 的点的序列，只要按照拓扑序选点，就一定能取遍序列中 所有的点。 于是发现这张图上入度不为0的点事实上都可以被选择。于是我们把所有入度不 为0的点排一下序，求前k个就可以了。时间复杂度 O(nlogn)，期望得分30。

子任务 4、5： 考虑DAG的情况放到普通有向图上会发生什么。 有了子任务 3 的提示，我们可以考虑把整个图缩点，将其变成一个DAG来做。 对于一个DAG，显然可以通过子任务 3 调整顺序的方式使得每个强连通分量的 选择情况除选点个数以外互不影响。故下面只讨论一个强连通分量内部的情况。 一个强连通分量显然可以看作是一棵外向树加上很多边得到的。 一棵外向树的定义：一个外向树的任意一个节点要么为叶节点，要么它与孩子 间的所有边都是由它指向孩子。 一棵外向树显然是一个 DAG 。按照之前对 DAG 上情况的说明，显然我们可以 选择除了根节点以外的任意节点。 因为一个强连通分量内部是互相连通的，于是我们不妨钦定一个点为根。 对于一个没有入度的强连通分量，我们不妨钦定点权最小的点为根。这样显然 选择的是最优的。 对于一个有入度的强连通分量，我们不妨钦定那个有入度的点为根。这样在选 择到只剩根节点的时候，因为根节点有入度，所以根节点是可以被选择的。于是这 个强连通分量可以被全部选择。这显然是最优的。 这样综合上述讨论，有入度的强连通分量可以随便选，没有入度的强连通分量 去掉最小的点权的点。剩下贪心取前 k 个就可以了。 进行一次 tarjan的复杂度是 O(n+m)，选前 k 个点可以排序一下。这样总复杂 度 O(m+nlogn)，期望得分 35 分。注意到复杂度瓶颈在排序上，考虑我们只需要前 k 大而不需要具体前 k 个之间的大小关系，于是使用 std::nth_element()函数可 以将复杂度降至 O(n+m)。期望得分 40 分。注意，输入规模到了 10e7 级别，需要 fread 来实现读入优化。

标程代码：

#include <cstdio>
#include <algorithm>
#include <functional>
#ifdef ONLINE_JUDGE
#define freopen(a, b, c)
#endif

typedef long long int ll;

namespace IPT {
  const int L = ;
  char buf[L], *front=buf, *end=buf;
  char GetChar() {
    if (front == end) {
      end = buf + fread(front = buf, , L, stdin);
      if (front == end) return -;
    }
    return *(front++);
  }
}

template <typename T>
inline void qr(T &x) {
  char ch = IPT::GetChar(), lst = ' ';
  while ((ch > '') || (ch < '')) lst = ch, ch=IPT::GetChar();
  while ((ch >= '') && (ch <= '')) x = (x << ) + (x << ) + (ch ^ ), ch = IPT::GetChar();
  if (lst == '-') x = -x;
}

const int maxn = ;

struct Edge {
  int v;
  Edge *nxt;

  Edge(const int _v, Edge *h) : v(_v), nxt(h) {}
};
Edge *hd[maxn];

int n, m, k, vistime, top, scnt;
int MU[maxn], dfn[maxn], low[maxn], stack[maxn], belong[maxn], minv[maxn];
bool instack[maxn], haveind[maxn];

void tarjan(const int u);

int main() {
  freopen("zay.in", "r", stdin);
  freopen("zay.out", "w", stdout);
  qr(n); qr(m); qr(k); MU[] = ;
  for (int i = ; i <= n; ++i) qr(MU[i]);
  for (int i = , u, v; i <= m; ++i) {
    u = v = ; qr(u); qr(v);
    hd[u] = new Edge(v, hd[u]);
  }
  for (int i = ; i <= n; ++i) if (!dfn[i]) {
    tarjan(i);
  }
  for (int u = ; u <= n; ++u) {
    for (auto e = hd[u]; e; e = e->nxt) if (belong[u] != belong[e->v]) {
      haveind[belong[e->v]] = true;
    }
  }
  for (int i = ; i <= scnt; ++i) if (!haveind[i]) {
    MU[minv[i]] = ;
  }
  std::nth_element(MU + , MU +  + k, MU +  + n, std::greater<int>());
  int ans = ;
  for (int i = ; i <= k; ++i) {
    ans += MU[i];
  }
  printf("%d\n", ans);
  return ;
}

void tarjan(const int u) {
  dfn[u] = low[u] = ++vistime;
  instack[stack[++top] = u] = true;
  for (auto e = hd[u]; e; e = e->nxt) {
    int v = e->v;
    if (!dfn[v]) {
      tarjan(v);
      low[u] = std::min(low[u], low[v]);
    } else if (instack[v]) {
      low[u] = std::min(low[u], dfn[v]);
    }
  }
  if (dfn[u] == low[u]) {
    int v, &_mv = minv[++scnt];
    do {
      instack[v = stack[top--]] = false;
      belong[v] = scnt;
      if (MU[v] < MU[_mv]) _mv = v;
    } while (v != u);
  }
}